目录
1.stack的介绍
2.queue的介绍
3.优先级队列（堆）
4.deque（双端队列）
1.stack的介绍
stack的文档介绍
翻译:
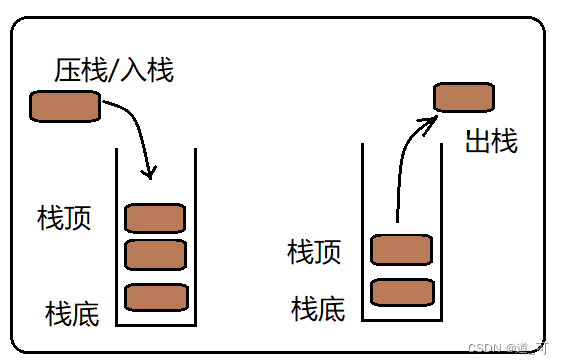
- 1. stack是一种容器适配器，专门用在具有后进先出操作的上下文环境中，其删除只能从容器的一端进行元素的插入与提取操作。
- 2. stack是作为容器适配器被实现的，容器适配器即是对特定类封装作为其底层的容器，并提供一组特定的成员函数来访问其元素，将特定类作为其底层的，元素特定容器的尾部(即栈顶)被压入和弹出。
- 3. stack的底层容器可以是任何标准的容器类模板或者一些其他特定的容器类，这些容器类应该支持以下
- 操作：
empty ：判空操作
size ：获取元素个数
back ：获取尾部元素操作
push_back ：尾部插入元素操作
pop_back ：尾部删除元素操作
- 4. 标准容器vector、deque、list均符合这些需求，默认情况下，如果没有为stack指定特定的底层容器，默认情况下使用deque。
stack 的接口
接口实现：
stack.h
template<class T, class Container = deque<T>>class stack{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_back();}const T& top(){return _con.back();}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};
2.queue的介绍
queue的文档介绍
翻译：
- 1. 队列是一种容器适配器，专门用于在FIFO上下文(先进先出)中操作，其中从容器一端插入元素，另一端提取元素。
- 2. 队列作为容器适配器实现，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素。元素从队尾入队列，从队头出队列。
- 3. 底层容器可以是标准容器类模板之一，也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:
empty ：检测队列是否为空
size ：返回队列中有效元素的个数
front ：返回队头元素的引用
back ：返回队尾元素的引用
push_back ：在队列尾部入队列
pop_front ：在队列头部出队列
- 4. 标准容器类deque和list满足了这些要求。默认情况下，如果没有为queue实例化指定容器类，则使用标准容器deque。
queue 的接口
接口实现：
queue.h
//适配器模式/配接器template<class T, class Container = deque<T>>class queue{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_front();}const T& front(){return _con.front();}const T& back(){return _con.back();}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};3.优先级队列（堆）
priority_queue的文档介绍
翻译：
- 1. 优先队列是一种容器适配器，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的。
- 2. 此上下文类似于堆，在堆中可以随时插入元素，并且只能检索最大堆元素(优先队列中位于顶部的元素)。
- 3. 优先队列被实现为容器适配器，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素。元素从特定容器的“尾部”弹出，其称为优先队列的顶部。
- 4. 底层容器可以是任何标准容器类模板，也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问，并支持以下操作：
empty()：检测容器是否为空
size()：返回容器中有效元素个数
front()：返回容器中第一个元素的引用
push_back()：在容器尾部插入元素
pop_back()：删除容器尾部元素
- 5. 标准容器类vector和deque满足这些需求。默认情况下，如果没有为特定的priority_queue类实例化指定容器类，则使用vector。
- 6. 需要支持随机访问迭代器，以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数make_heap、push_heap和pop_heap来自动完成此操作。
priority_queue的使用
优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。注意：默认情况下priority_queue是大堆。
| 函数声明 | 接口说明 |
| priority_queue() | 构造一个空的优先级队列 |
| empty() | 检测优先级队列是否为空，是返回 true ，否则返回 false |
| top() | 返回优先级队列中最大 ( 最小元素 ) ，即堆顶元素 |
| push() | 在优先级队列中插入元素 x |
| pop() | 删除优先级队列中最大 ( 最小 ) 元素，即堆顶元素 |
代码演示：
#include <iostream>#include <vector>#include <functional>#include <queue>using namespace std;int main()
{vector<int> v{3, 7, 4, 2, 5, 6, 8, 9, 1, 0};//默认大堆priority_queue<int> pq; //大于仿函数 - 小堆//priority_queue<int, vector<int>, greater<int>> pq; for (auto e : v){pq.push(e);}while (!pq.empty()){cout << pq.top() << " ";pq.pop();}cout << endl;return 0;
}大堆输出：
小堆输出：
接口实现：
template<class T, class Container = vector<T>>class priority_queue{public:void push(const T& x){_con.push_back(x);Adjust_up(_con.size() - 1); }void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();Adjust_down(0); }const T& top(){return _con[0];}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};堆的插入: (演示图表为小堆）
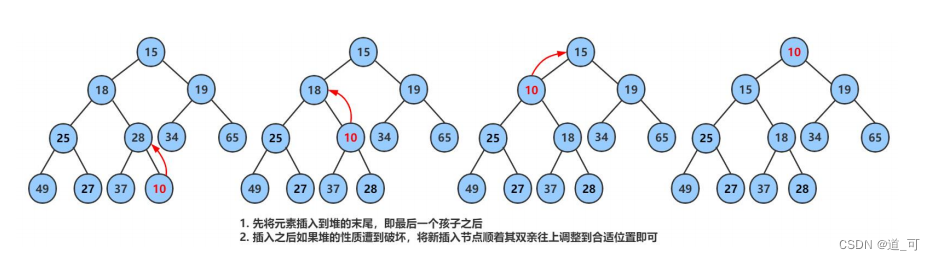
代码实现：向上调整
void Adjust_up(int child){int parent = (child - 1) / 2;while (child > 0){if (_con[child] > _con[parent]){swap(_con[child], _con[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}堆的删除：(演示图表为小堆）
代码实现：向下调整
void Adjust_down(int parent){size_t child = parent * 2 + 1;while (child < _con.size()){//child + 1 < _con.size() 是为了防止右孩子越界if (child + 1 < _con.size() && _con[child + 1] > _con[child]) {child++;}if (_con[child] > _con[parent]){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}完整代码：
priority_queue.h 初始版本
template<class T, class Container = vector<T>>class priority_queue{public:// 向上调整void Adjust_up(int child){int parent = (child - 1) / 2;while (child > 0){if (_con[child] > _con[parent]){swap(_con[child], _con[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}void push(const T& x){_con.push_back(x);Adjust_up(_con.size() - 1); }//向下调整void Adjust_down(int parent){size_t child = parent * 2 + 1;while (child < _con.size()){//child + 1 < _con.size() 是为了防止右孩子越界if (child + 1 < _con.size() && _con[child + 1] > _con[child]) {child++;}if (_con[child] > _con[parent]){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();Adjust_down(0); }const T& top(){return _con[0];}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};//--------------------------------------------------------------void test_priority_queue(){vector<int> v{3, 7, 4, 2, 5, 6, 8, 9, 1, 0};//默认大堆priority_queue<int> pq; for (auto e : v){pq.push(e);}while (!pq.empty()){cout << pq.top() << " ";pq.pop();}cout << endl;}运行结果：
至此，完成priority_queue初始版本，但是这里存在一个问题，以上代码默认实现的是大堆，那如何修改为小堆呢？每次去修改向上/向下调整代码也能实现，但是太过繁琐，而在 stl 库里面，这里运用了一个语法：传入第三个模板参数---仿函数
进阶完整版代码如下：
priority_queue.h
#pragma oncenamespace dwr
{template<class T>class less{public:bool operator()(const T& x, const T& y){return x < y;}};template<class T>class greater{public:bool operator()(const T& x, const T& y){return x > y;}};template<class T, class Container = vector<T>, class Comapre = less<T>>class priority_queue{public:// 向上调整void Adjust_up(int child){Comapre com;int parent = (child - 1) / 2;while (child > 0){//if (_con[child] > _con[parent])if(com(_con[parent], _con[child])) // 注意： 默认是less 小于{swap(_con[child], _con[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}void push(const T& x){_con.push_back(x);Adjust_up(_con.size() - 1); }//向下调整void Adjust_down(int parent){Comapre com;size_t child = parent * 2 + 1;while (child < _con.size()){//child + 1 < _con.size() 是为了防止右孩子越界//if (child + 1 < _con.size() && _con[child + 1] > _con[child]) if (child + 1 < _con.size() && Comapre()( _con[child] , _con[child + 1])) //这里是匿名对象调用operator[]{child++;}if (com(_con[parent] , _con[child])){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();Adjust_down(0); }const T& top(){return _con[0];}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};//--------------------------------------------------------------void test_priority_queue(){vector<int> v{3, 7, 4, 2, 5, 6, 8, 9, 1, 0};//大于仿函数 - 小堆priority_queue<int, vector<int>, greater<int>> pq;for (auto e : v){pq.push(e);}while (!pq.empty()){cout << pq.top() << " ";pq.pop();}cout << endl;}}test.cpp
#include <iostream>#include <vector>#include <functional>#include <queue>using namespace std;#include "priority_queue.h"int main()
{dwr::test_priority_queue();return 0;
}例：
因为priority_queue的底层结构就是堆，因此此处只需对通用的进行封装即可。
4.deque（双端队列）
deque文档介绍
deque其实是一种容器适配器，那么什么是适配器？
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结)，该种模式是将一个类的接口转换成客户希望的另外一个接口。
STL标准库中stack和queue的底层结构
虽然stack和queue中也可以存放元素，但在STL中并没有将其划分在容器的行列，而是将其称为容器适配器，这是因为stack和队列只是对其他容器的接口进行了包装，STL中stack和queue默认使用deque，比如：
deque的简单介绍
deque的原理介绍
deque(双端队列)：是一种双开口的"连续"空间的数据结构，双开口的含义是：可以在头尾两端进行插入和删除操作，且时间复杂度为O(1)，与vector比较，头插效率高，不需要搬移元素；与list比较，空间利用率比较高。
deque并不是真正连续的空间，而是由一段段连续的小空间拼接而成的，实际deque类似于一个动态的二维数组，其底层结构如下图所示：
双端队列底层是一段假象的连续空间，实际是分段连续的，为了维护其“整体连续”以及随机访问的假象，落在了deque的迭代器身上，因此deque的迭代器设计就比较复杂，如下图所示：
那deque是如何借助其迭代器维护其假想连续的结构呢？
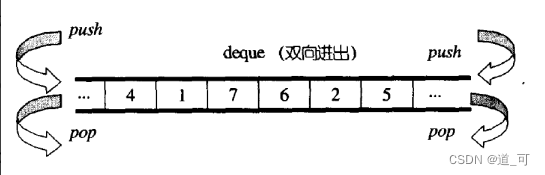
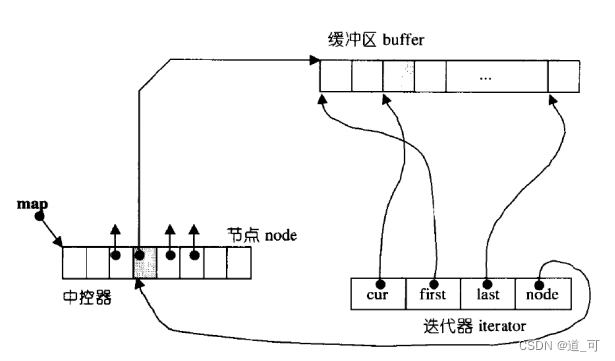
deque的缺陷
与vector比较，deque的优势是：头部插入和删除时，不需要搬移元素，效率特别高，而且在扩容时，也不需要搬移大量的元素，因此其效率是必vector高的。
与list比较，其底层是连续空间，空间利用率比较高，不需要存储额外字段。
但是，deque有一个致命缺陷：不适合遍历，因为在遍历时，deque的迭代器要频繁的去检测其是否移动到某段小空间的边界，导致效率低下，而序列式场景中，可能需要经常遍历，因此在实际中，需要线性结构时，大多数情况下优先考虑vector和list，deque的应用并不多，而目前能看到的一个应用就是，STL用其作为stack和queue的底层数据结构。
为什么选择deque作为stack和queue的底层默认容器？
stack是一种后进先出的特殊线性数据结构，因此只要具有 push_back() 和 pop_back() 操作的线性结构，都可以作为stack的底层容器，比如vector和list都可以；queue是先进先出的特殊线性数据结构，只要具有 push_back 和 pop_front 操作的线性结构，都可以作为queue的底层容器，比如 list。但是STL中对stack和queue默认选择deque作为其底层容器，主要是因为：
1. stack和queue不需要遍历(因此stack和queue没有迭代器)，只需要在固定的一端或者两端进行操作。
2. 在stack中元素增长时，deque比vector的效率高(扩容时不需要搬移大量数据)；queue中的元素增长时，deque不仅效率高，而且内存使用率高。
结合了deque的优点，而完美的避开了其缺陷
以上仅代表个人观点，欢迎讨论
