【数据结构入门精讲 | 第五篇】栈知识点及考研408、企业面试练习-编程知识

在上一篇中我们进行了表的专项练习，在这篇文章中我们将介绍栈的相关知识点。

在这里插入图片描述

基础概念

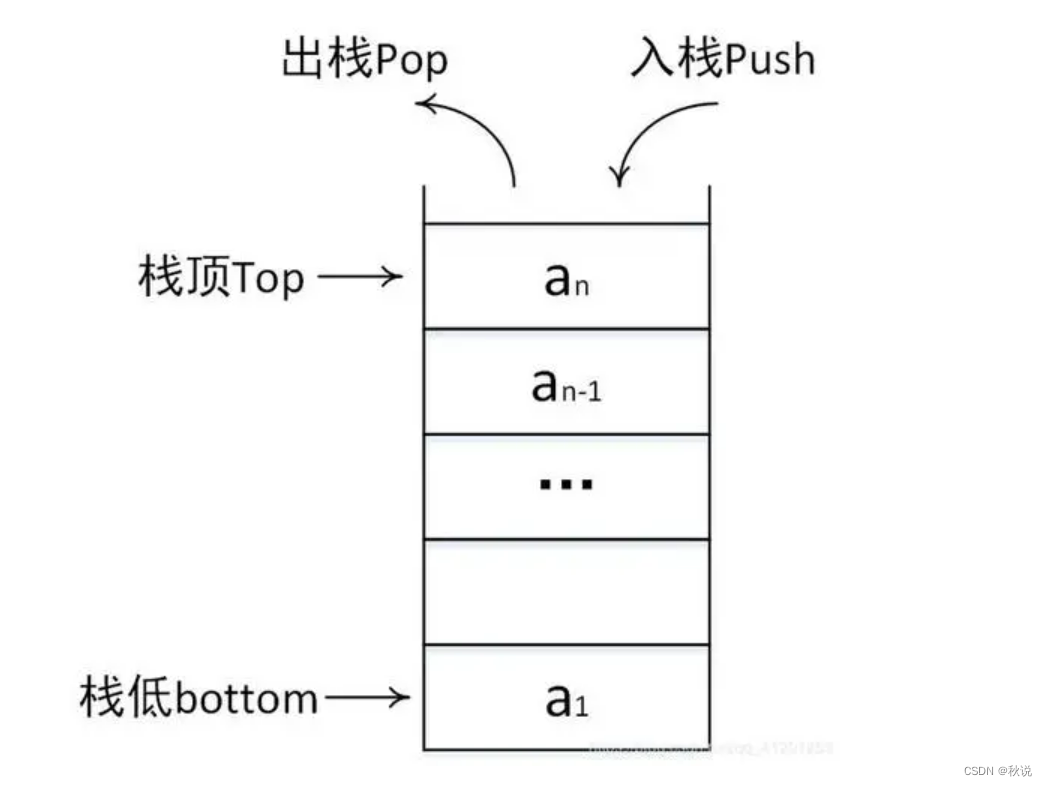
栈是限定仅在栈顶（即表首）进行插入和删除操作的线性表，也称为后进先出（Last In First Out）的线性表，简称 LIFO 结构。

栈的内部实现原理其实就是数组或链表的操作，而之所以引入栈这个概念，是为了将程序设计问题模型化，利用栈的先进后出特性对特定的一些问题进行简化。（栈是线性表的特例）

允许插入和删除元素的一端称为栈顶，另一端称为栈底，不含任何任何数据元素的栈称为空栈。

在这里插入图片描述

顺序栈

当使用线性表的顺序存储结构（即数组）实现栈时，该栈被称为顺序栈

伪代码

//创建一个容量为size的空栈
Stack StackInit(int size)
{ Stack S=malloc(sizeof *S);
S->data=malloc(size *sizeof(StackItem));
S->maxtop=size-1;
S->top=-1;
return S;
}//判断栈空StackEmpty(S)
int StackEmpty (Stack S) 
{return S->top<0;}//top=-1时为空栈// 判断栈满StackFull(S)
int StackFull (Stack S) 
{return S->top==S->maxtop;}//top==maxtop时为满栈//释放空间StackFree(S)
int StackFree (Stack S) {free(S->data); free(S);}//返回栈顶元素StackItem StackTop(Stack S)
{ if (StackEmpty(S)) Error("Stack is empty");
else
return S->data[S->top]; //直接返回栈顶top元素即可
}//入栈操作push(x,S)
void Push (StackItem x, Stack S)
{ if (StackFull(S)) Error("Stack is full");
else S->data[++S->top]=x;}//前置自加
//x为新的栈顶元素，存放在插⼊前的top+1单元//出栈操作Pop(S)
void Pop (Stack S)
{ if (StackEmpty(S)) Error("Stack is empty ");
else return S->data[S->top--];}//后置自减
//删除栈顶元素x后，新的栈顶位置为删除前的top-1单元

注意点：当使用数组存储栈的时候，设数组大小为M，当栈为空时，栈顶指针值为-1，当栈满时，栈顶指针为M-1。若此时入栈，则上溢（overflow)

链栈

当使用线性表的链式存储结构（单链表）实现栈时，该栈被称为链栈。为维护堆栈的FILO的存储特性，链栈中维护的top指针始终指向栈顶元素。

伪代码

//空栈的创建
Stack StackInit()
{ Stack S=malloc(sizeof *S);
S->top=0;//将top置为空指针，创建一个空栈
return S;
}//o(1)//检查是否空栈StackEmpty(S)
int StackEmpty (Stack S)
{//检测top是否为空指针
return S->top==0;
}//返回栈顶元素
StackItem StackTop(Stack S)
{
if (StackEmpty(S))
Error("Stack is empty");
else return S->top->element;
}//插入元素
void Push(StackItem x, Stack S)
{ slink p;
if (StackFull(S)) Error("Stack is Full");
p=NewStackNode();//为元素x创建一个新结点
p->element=x;
p->next=S->top;//修改栈顶结点指针top
S->top=p;//新结点成为新的栈顶指针top
}//删除元素
StackItem Pop(Stack S)
{ slink p; StackItem x;
if (StackEmpty(S)) Error("Stack is empty");
x=S->top->element;//将栈顶指针top所指元素放入x中
p=S->top;
S->top=p->next;//修改栈顶指针使其指向栈顶元素的下一个结点
free(p);
return x;
}

顺序栈与链栈的异同点：顺序栈和链栈的时间复杂度均为O(1)
为了使每个栈在算法运行过程中不会溢出，通常要为每个栈预置一个较大的栈空间，但它的优势是存取时定位很方便。

链栈要求每个元素都要配套一个指向下个结点的指针域，增大了内存开销，但好处是栈的长度无限，因此，如果栈的使用过程中元素变化不可预料，有时很小，有时很大，那么最好使用链栈。反之，如果它的变化在可控范围内，则建议使用顺序栈。

接下来让我们进行栈的相关练习。

判断题

1.若一个栈的输入序列为1，2，3，…，N，输出序列的第一个元素是i，则第j个输出元素是j−i−1。（错）

解析：不确定，如果输出的第一个是1，则第二个可以是任何数。

2.栈结构不会出现溢出现象。（错）

链式存储的栈结构不会溢出，但顺序存储的栈结构会溢出，因为它一开始就定义了栈的长度。

3.若一个栈的输入序列为{1, 2, 3, 4, 5}，则不可能得到{3, 4, 1, 2, 5}这样的出栈序列。（对）

结合题目且1比2先入栈，所以出栈的顺序肯定是2在1前面，所以不可能得到{3, 4, 1, 2, 5}

4.两个栈共享一片连续空间，可以将两个栈的栈底分别设在这片空间的两端。（对）

选择题

1.若采用带头、尾指针的单向链表表示一个堆栈，那么该堆栈的栈顶指针top应该如何设置？
A.随便哪端作为top都可以
B.链表头、尾都不适合作为top
C.将链表头设为top
D.将链表尾设为top
选C，解析：栈顶为表首，即链表头。

2.给定有限符号集 S , in 和 out 均为 S 中所有元素的任意排列。对于初始为空的栈 ST, 下列叙述中，正确的是：（选A）
A.若 in 是 ST 的入栈序列，out 是对应 in 的出栈序列，则 in 与 out 可能互为倒序
B.若 out 是 ST 的出栈序列，则不能判断 in 是否为其可能的入栈序列
C.若 in 是 ST 的入栈序列，out 是对应 in 的出栈序列，则 in 与 out 一定不同
D.若 in 是 ST 的入栈序列，则不能判断 out 是否为其可能的出栈序列

3.将5个字母ooops按此顺序入栈，则有多少种不同的出栈顺序可以仍然得到ooops？（选A）
A.5
B.3
C.1
D.6

解析：

o1进o1出、o2进o2出、o3进o3出
o1进o2进、o2出o1出、o3进o3出
o1进o2进、o2出o3进、o3出o1出
o1、o2、o3进，o3、o2、o1出
o1进o1出、o2进o3进、o3出o2出

4.下列关于栈的叙述中，错误的是：1. 采用非递归方式重写递归程序时必须使用栈
2. 函数调用时，系统要用栈保存必要的信息
3. 只要确定了入栈次序，即可确定出栈次序
4. 栈是一种受限的线性表，允许在其两端进行操作解析：计算斐波拉契数列迭代实现只需要一个循环即可实现，故1错
2对。3错，不做过多解释。4错，栈是一种受限的线性表，只允许在一端进行操作。

5.若一个栈的入栈序列为1、2、3、…、N，其输出序列为p1、p2、p3、…、pN。若p1=N，则pi为：（）
解析：栈的特点是后进先出，入栈序列是 1,2,3,…,n，输出对应的应该是 n,n-1,n-2,…,1，所以答案是 n - i + 1。

6.给定一个堆栈的入栈序列为{ 1, 2, ⋯, n }，出栈序列为{ p1, p2, ⋯, pn }。如果p2=n，则存在多少种不同的出栈序列？
解析：在n出栈之前，前n-1个元素都可以第一个出栈，所以答案为n-1。

7.若元素a、b、c、d、e、f依次进栈，允许进栈、退栈操作交替进行，但不允许连续三次进行退栈工作，则不可能得到的出栈序列是？（D）
A.c b d a e f
B.b c a e f d
C.d c e b f a
D.a f e d c b
解析：假设选项成立，推得其操作即可。

8.在作进栈运算时，应先判别栈是否(① )；在作退栈运算时应先判别栈是否(② )。当栈中元素为n个，作进栈运算时发生上溢，则说明该栈的最大容量为(③ )。
①: A. 空 B. 满 C. 上溢 D. 下溢
②: A. 空 B. 满 C. 上溢 D. 下溢
③: A. n-1 B. n C. n+1 D. n/2
A. ① B ② A ③ A
B. ① C ② D ③ B
C. ① B ② A ③ B
D. ① B ② B ③ A
答案选C，解析：在作进栈运算时，应先判别栈是否满。在作退栈运算时应先判别栈是否空。当栈中元素为n个，作进栈运算时发生上溢，则说明该栈的最大容量为n。

9.若一个栈的入栈序列为1、2、3、…、N，输出序列的第一个元素是i，则第j个输出元素是：
A.不确定
B.i−j
C.i−j−1
D.j−i−1
选A，解析：i如果是1，则第j个输出的元素可以是2~N任何一个。

10.设一个堆栈的入栈顺序是1、2、3、4、5。若第一个出栈的元素是4，则最后一个出栈的元素必定是：
A.3
B.1或者5
C.5
D.1
选B，解析：第一个出栈的元素是4，说明这时候5还没入栈，所以下一步可能是入栈或者出栈。

11.检查表达式中的括号是否匹配的问题需要借助________来解决。
A.有向无环图
B.队列
C.二叉搜索树
D.堆栈
选D，解析：具体解析可看后面的编程题。

12.若借助堆栈将中缀表达式a+b*c+(d*e+f)*g转换为后缀表达式，当读入f时，堆栈里的内容是什么（按堆栈自底向上顺序）？
A.+(*+
B.abcde
C.++(+
D.+(+

当输入的是操作数时，直接输出a;
遇到操作符，如果栈为空入栈，+入栈
当输入的是操作数时，直接输出b;
栈顶元素+的优先级小于*的优先级，* 压栈;
当输入的是操作数时，直接输出c;
当输入的是运算符，栈顶元素*的优先级大于+的优先级，* 出栈;循环，栈顶元素+的优先级等于+的优先级，+ 出栈，+入栈；
当输入的是开括号时，把它压栈;
当输入的是操作数时，直接输出d;
当输入的是运算符，因为栈顶是开括号，* 压栈；
当输入的是操作数时，直接输出e;
当输入的是运算符，栈顶元素*的优先级大于+的优先级，* 出栈;+入栈；

当输入的是f停止，此时栈中+(+

总而言之

如果在外面的符号比栈顶符号优先级要高，则入栈
如果外面的小于等于栈顶的，则栈顶出栈；接着再把这个外面的和第二个栈元素比较

13.设有一顺序栈S，元素s1,s2,s3,s4,s5,s6依次进栈，如果6个元素出栈的顺序是s2,s3,s4, s6 , s5,s1,则栈的容量至少应该是( )。
A.3
B.5
C.6
D.2
选A，解析：首先给一个容量让1进，再给一个容量让2进，2出，3进，此时3占有的是第二个容量，3出，4进，此时4占有的是第二个容量，4出，5进，此时5占有的是第二个容量，再给一个容量让6进，此时6占有的是第三个容量，然后依次出栈。所以栈的容量至少是3个。

14.利用大小为n的数组（下标从0到n-1）存储一个栈时，假定栈从数组另一头开始且top==n表示栈空，则向这个栈插入一个元素时，修改top指针应当执行：
A.top–
B.top不变
C.top=0
D.top++
选A，解析：插入元素时，栈的top指针应上移，而该栈存储在数组中，故top的表现形式为top–。

15.元素A,B,C,D依次入栈，出栈无限制，则以下（）是可能的出栈序列。
A. C, A, B, D
B. B, D, A, C
C. A, D, B, C
D. B, A, D, C
选D，解析：对于A，如果C第一个出栈，则A的出栈顺序应该在B后；对于B，如果B,D先后出栈，则说明A的出栈次序应该在C后；对C，如果D在第二个出栈，则说明B的出栈次序应该在C后；D正确。

16.与数据存储结构无关的概念是
A.栈 B.链表 C.顺序表 D.二叉链表
选A，栈可以数组实现也可以链表实现。

17.设指针变量top指向当前链式栈的栈顶，则删除栈顶元素的操作序列为（ D ）。
A. top=top+1; B. top=top-1;
C. top->next=top; D. top=top->next;

解析：
top->next指向的是空
把top赋为空
即完成了删除操作

填空题

1.用 S 表示进栈操作，用 X 表示出栈操作，若元素的进栈顺序是 1，2，3，4，出栈顺序是 1，3，4，2，则相应的操作序列为（SXSSXSXX）

2.求该后缀表达式的值：9 2 3 + - 10 2 / -
解：方法是遇到运算符时取前面两个元素进行运算。
即23与+得到5，表达式变为

9 5 - 10 2 / -

9 5 - 得到4，表达式变为

4 10 2 / -

最后得到-1

3.求中缀表达式（3+4*x）-2*y/3的后缀表达式
解：（入栈，3输出，+入栈，4输出，的优先级大于+，*入栈
x输出，遇到），依次出栈，所以和+依次出栈
-入栈 2输出入栈 y输出 /优先级等于*
所以出栈 /入栈 3输出
最后\出栈 -出栈
所以后缀表达式为：

34x*+2y*3/-

4.请把一个十进制数N转换为d进制数,并输出。

在这里插入图片描述

函数题

R6-1 在一个数组中实现两个堆栈

本题要求在一个数组中实现两个堆栈。

函数接口定义：

Stack CreateStack( int MaxSize );
bool Push( Stack S, ElementType X, int Tag );
ElementType Pop( Stack S, int Tag );

其中Tag是堆栈编号，取1或2；MaxSize堆栈数组的规模；Stack结构定义如下：

typedef int Position;
struct SNode {ElementType *Data;Position Top1, Top2;int MaxSize;
};
typedef struct SNode *Stack;

注意：如果堆栈已满，Push函数必须输出“Stack Full”并且返回false；如果某堆栈是空的，则Pop函数必须输出“Stack Tag Empty”（其中Tag是该堆栈的编号），并且返回ERROR。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>#define ERROR 1e8
typedef int ElementType;
typedef enum { push, pop, end } Operation;
typedef enum { false, true } bool;
typedef int Position;
struct SNode {ElementType *Data;Position Top1, Top2;int MaxSize;
};
typedef struct SNode *Stack;Stack CreateStack( int MaxSize );
bool Push( Stack S, ElementType X, int Tag );
ElementType Pop( Stack S, int Tag );Operation GetOp();  /* details omitted */
void PrintStack( Stack S, int Tag ); /* details omitted */int main()
{int N, Tag, X;Stack S;int done = 0;scanf("%d", &N);S = CreateStack(N);while ( !done ) {switch( GetOp() ) {case push: scanf("%d %d", &Tag, &X);if (!Push(S, X, Tag)) printf("Stack %d is Full!\n", Tag);break;case pop:scanf("%d", &Tag);X = Pop(S, Tag);if ( X==ERROR ) printf("Stack %d is Empty!\n", Tag);break;case end:PrintStack(S, 1);PrintStack(S, 2);done = 1;break;}}return 0;
}/* 你的代码将被嵌在这里 */

输入样例：

5
Push 1 1
Pop 2
Push 2 11
Push 1 2
Push 2 12
Pop 1
Push 2 13
Push 2 14
Push 1 3
Pop 2
End

输出样例：

Stack 2 Empty
Stack 2 is Empty!
Stack Full
Stack 1 is Full!
Pop from Stack 1: 1
Pop from Stack 2: 13 12 11

Stack CreateStack(int MaxSize) {// 创建一个双栈，并返回指向该双栈的指针Stack S = (Stack)malloc(sizeof(struct SNode));// 使用动态内存分配来分配栈所需的空间S->Data = (ElementType*)malloc(MaxSize * sizeof(ElementType));S->Top1 = -1;S->Top2 = MaxSize;S->MaxSize = MaxSize;return S;
}bool Push(Stack S, ElementType X, int Tag) {// 如果双栈已满，则打印 "Stack Full" 并返回 falseif (S->Top1 + 1 == S->Top2) {printf("Stack Full\n");return false;}// 如果 Tag 为 1，则将元素 X 压入栈1if (Tag == 1) {S->Data[++S->Top1] = X;}// 如果 Tag 不为 1，则将元素 X 压入栈2else {S->Data[--S->Top2] = X;}return true;
}ElementType Pop(Stack S, int Tag) {// 如果 Tag 为 1，则从栈1弹出一个元素if (Tag == 1) {// 如果栈1为空，则打印 "Stack 1 Empty" 并返回 ERRORif (S->Top1 == -1) {printf("Stack 1 Empty\n");return ERROR;}return S->Data[S->Top1--];}// 如果 Tag 不为 1，则从栈2弹出一个元素else if (Tag == 2) {// 如果栈2为空，则打印 "Stack 2 Empty" 并返回 ERRORif (S->Top2 == S->MaxSize) {printf("Stack 2 Empty\n");return ERROR;}return S->Data[S->Top2++];}
}

编程题

R7-1 汉诺塔的非递归实现

借助堆栈以非递归（循环）方式求解汉诺塔的问题（n, a, b, c），即将N个盘子从起始柱（标记为“a”）通过借助柱（标记为“b”）移动到目标柱（标记为“c”），并保证每个移动符合汉诺塔问题的要求。

输入格式:

输入为一个正整数N，即起始柱上的盘数。

输出格式:

每个操作（移动）占一行，按柱1 -> 柱2的格式输出。

输入样例:

输出样例:

a -> c
a -> b
c -> b
a -> c
b -> a
b -> c
a -> c

#include<stdio.h>
using namespace std;void move(int n, char a, char b, char c);
int main()
{int n;scanf("%d", &n);move(n,'a','b','c');return 0;
}
void move(int n,char a,char b,char c)
{if(n==1){printf("%c -> %c\n",a,c);}  else{move(n-1,a,c,b);  printf("%c -> %c\n",a,c);move(n-1,b,a,c);  }
}

R7-2 表达式转换

算术表达式有前缀表示法、中缀表示法和后缀表示法等形式。日常使用的算术表达式是采用中缀表示法，即二元运算符位于两个运算数中间。请设计程序将中缀表达式转换为后缀表达式。

输入格式:

输入在一行中给出不含空格的中缀表达式，可包含+、-、*、/以及左右括号()，表达式不超过20个字符。

输出格式:

在一行中输出转换后的后缀表达式，要求不同对象（运算数、运算符号）之间以空格分隔，但结尾不得有多余空格。

输入样例:

2+3*(7-4)+8/4

输出样例:

2 3 7 4 - * + 8 4 / +

#include <stdio.h>
#include <string.h>
#include <stdlib.h>// 定义堆栈结构体
typedef struct snode* stack;
struct snode {char ch[20];int top; // 定义堆栈顶指针
};stack CreatStack() // 创建堆栈函数
{stack s = (stack)malloc(sizeof(struct snode));s->top = -1; // 初始化栈顶指针return s;
}void push(stack s, char c) // 入栈函数
{(s->top)++;s->ch[s->top] = c;
}char pop(stack s) // 出栈函数
{return s->ch[(s->top)--];
}int main()
{   char s[21]; // 输入表达式的字符串，假设长度不超过20scanf("%s", s);int l = strlen(s); // 获取输入字符串的长度char ch1[150]; // 存储符号优先级的数组ch1['('] = 0;ch1['+'] = ch1['-'] = 1;ch1['*'] = ch1['/'] = 2;stack st = CreatStack(); // 创建堆栈int flag = 0; // 控制格式输出的标志变量，初始为0for (int i = 0; i < l; i++) // 遍历输入字符串{if (s[i] == '(') // 如果当前字符是左括号，则直接入栈push(st, s[i]);else if (s[i] == ')') // 如果当前字符是右括号，则弹出堆栈中所有元素，直到遇到左括号为止{char t;t = pop(st);while (t != '(') // 循环弹出，直到遇到左括号{printf(" %c", t); // 输出当前符号t = pop(st);}flag = 1; // 标记需要在下一次输出前添加空格}else if (s[i] == '+' || s[i] == '-' || s[i] == '*' || s[i] == '/') // 如果当前字符是运算符{if (s[i] == '+' && (s[i - 1] == '(' || i == 0)) // 如果当前运算符是正号（表示正数），则不进行操作;else if (s[i] == '-' && (s[i - 1] == '(' || i == 0)) // 如果当前运算符是负号（表示负数），则直接输出{printf("-");}else if (ch1[s[i]] > ch1[st->ch[st->top]] || st->top == -1) // 如果当前运算符优先级高于栈顶运算符或者堆栈为空，则直接入栈{push(st, s[i]);flag = 1; // 标记需要在下一次输出前添加空格}else // 如果当前运算符优先级低于等于栈顶运算符，则弹出堆栈中优先级高于或等于当前运算符的所有元素，并将当前运算符入栈{printf(" %c", pop(st)); // 输出堆栈中优先级高于或等于当前运算符的元素while (ch1[s[i]] <= ch1[st->ch[st->top]] && st->top != -1) // 循环弹出符合条件的元素{printf(" %c", pop(st));}push(st, s[i]); // 将当前运算符入栈flag = 1; // 标记需要在下一次输出前添加空格}}else // 如果当前字符是操作数，直接输出{if (flag) // 如果前一个字符是右括号或者运算符，则在输出当前操作数前添加空格{printf(" ");flag = 0;}printf("%c", s[i]);}}while (st->top != -1) // 将堆栈中剩余的元素全部输出{printf(" %c", pop(st));}
}

R7-3 出栈序列的合法性

给定一个最大容量为 M 的堆栈，将 N 个数字按 1, 2, 3, …, N 的顺序入栈，允许按任何顺序出栈，则哪些数字序列是不可能得到的？例如给定 M=5、N=7，则我们有可能得到{ 1, 2, 3, 4, 5, 6, 7 }，但不可能得到{ 3, 2, 1, 7, 5, 6, 4 }。

输入格式：

输入第一行给出 3 个不超过 1000 的正整数：M（堆栈最大容量）、N（入栈元素个数）、K（待检查的出栈序列个数）。最后 K 行，每行给出 N 个数字的出栈序列。所有同行数字以空格间隔。

输出格式：

对每一行出栈序列，如果其的确是有可能得到的合法序列，就在一行中输出YES，否则输出NO。

输入样例：

5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2

输出样例：

YES
NO
NO
YES
NO

这是“火车进站问题”（也有一些人称之为“火车调度问题”）的抽象化题目。

题意：有 n 辆火车需要进站，每辆火车按照编号依次从 1 到 n 进站，每次只能进一辆或出一辆火车，而且进站的火车必须先出站，随时可以查看站内的顺序。问是否可能按照某种顺序将所有火车进站并出站。

解题思路：这是一道典型的模拟题目。我们可以使用一个栈来模拟火车进站和出站的过程。具体思路如下：

初始化一个栈，用于模拟火车站内的火车顺序，同时初始化一个指针 jin，用于表示下一辆要进站的火车编号，以及一个指针 chu，用于表示下一辆要出站的火车编号。
依次读入 n 辆火车的编号，将它们保存在一个数组中。
进入循环，如果 jin 等于当前要出站的火车编号 a[chu]，则直接将 jin 和 chu 都加 1；否则，如果栈不为空且栈顶元素等于当前要出站的火车编号 a[chu]，则弹出栈顶元素，将 chu 加 1；否则，将 jin 入栈，并将 jin 加 1。
循环结束后，如果栈为空，则说明所有火车都已经进站出站，输出 YES；否则，输出 NO。

m 表示栈的最大容量，也就是火车站内最多能同时停放的火车数量。

#include <stdio.h>int main()
{int m, n, k;scanf("%d%d%d", &m, &n, &k);int a[1000], stack[1000];for (int i = 0; i < k; i++){int jin = 1, chu = 1, top = 0, flag = 1;for (int j = 1; j <= n; i++){scanf("%d", &a[j]);}while (1){if (jin == a[chu]){jin++;chu++;}else if (top != 0 && a[chu] == stack[top - 1]){top--;chu++;}else{if (jin > n)break;stack[top++] = jin;jin++;if (top >= m){flag = 0;break;}}}if (flag == 0 || top != 0)printf("NO\n");elseprintf("YES\n");}
}方法二：#include<bits/stdc++.h>
using namespace std;
int main(){int m,n,k;cin>>m>>n>>k;stack<char> s;while(k--){int q=1,flag=0;int a[n];for(int i=0;i<n;i++)cin>>a[i];for(int i=0;i<n;i++){if(s.size()>0&&s.top()==a[i])s.pop();else{if(q>a[i]){flag=1;break;}for(;q<a[i];q++){s.push(q);}if(s.size()>=m){flag=1;break;}q=a[i]+1;}}if(flag)cout<<"NO"<<endl;else cout<<"YES"<<endl;while(!s.empty()) s.pop();}return 0;
}

R7-4 包装机

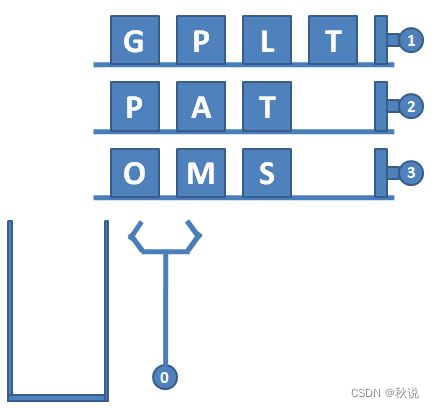
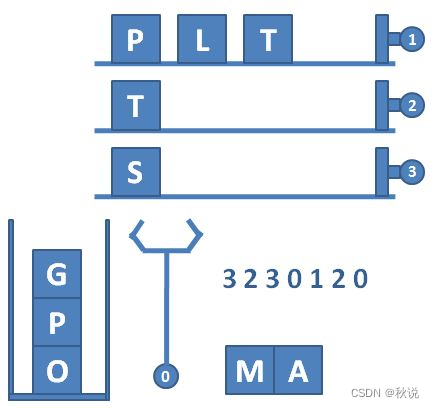
一种自动包装机的结构如图 1 所示。首先机器中有 N 条轨道，放置了一些物品。轨道下面有一个筐。当某条轨道的按钮被按下时，活塞向左推动，将轨道尽头的一件物品推落筐中。当 0 号按钮被按下时，机械手将抓取筐顶部的一件物品，放到流水线上。图 2 显示了顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态。

在这里插入图片描述

一种特殊情况是，因为筐的容量是有限的，当筐已经满了，但仍然有某条轨道的按钮被按下时，系统应强制启动 0 号键，先从筐里抓出一件物品，再将对应轨道的物品推落。此外，如果轨道已经空了，再按对应的按钮不会发生任何事；同样的，如果筐是空的，按 0 号按钮也不会发生任何事。

现给定一系列按钮操作，请你依次列出流水线上的物品。

输入格式：

输入第一行给出 3 个正整数 N（≤100）、M（≤1000）和 Smax（≤100），分别为轨道的条数（于是轨道从 1 到 N 编号）、每条轨道初始放置的物品数量、以及筐的最大容量。随后 N 行，每行给出 M 个英文大写字母，表示每条轨道的初始物品摆放。

最后一行给出一系列数字，顺序对应被按下的按钮编号，直到 −1 标志输入结束，这个数字不要处理。数字间以空格分隔。题目保证至少会取出一件物品放在流水线上。

输出格式：

在一行中顺序输出流水线上的物品，不得有任何空格。

输入样例：

3 4 4
GPLT
PATA
OMSA
3 2 3 0 1 2 0 2 2 0 -1

输出样例：

MATA

#include<bits/stdc++.h>
using namespace std;
int n,m,s;
queue<char>q[110];
stack<char>st;
int main(){cin>>n>>m>>s;for(int i=1;i<=n;i++){string a;cin>>a;for(int j=0;j<a.length();j++){q[i].push(a[j]);}}int a;while(cin>>a,a!=-1){if(a==0){if(st.size()){ // 如果栈不为空，输出栈顶元素并出栈cout<<st.top();st.pop();}}else{if(st.size()==s){ // 如果栈已满，执行出栈和入轨道操作if(q[a].size()){ // 如果轨道a有物品才进行操作cout<<st.top(); // 输出栈顶元素st.pop(); // 出栈int t=q[a].front(); // 获取轨道a的首个元素q[a].pop(); // 出队st.push(t); // 入栈}}else{ // 如果栈未满，执行入栈操作if(q[a].size()){ // 如果轨道a有物品才进行操作int t=q[a].front(); // 获取轨道a的首个元素q[a].pop(); // 出队st.push(t); // 入栈}}}}return 0;
}

R7-1 彩虹瓶

在这里插入图片描述
彩虹瓶的制作过程（并不）是这样的：先把一大批空瓶铺放在装填场地上，然后按照一定的顺序将每种颜色的小球均匀撒到这批瓶子里。

假设彩虹瓶里要按顺序装 N 种颜色的小球（不妨将顺序就编号为 1 到 N）。现在工厂里有每种颜色的小球各一箱，工人需要一箱一箱地将小球从工厂里搬到装填场地。如果搬来的这箱小球正好是可以装填的颜色，就直接拆箱装填；如果不是，就把箱子先码放在一个临时货架上，码放的方法就是一箱一箱堆上去。当一种颜色装填完以后，先看看货架顶端的一箱是不是下一个要装填的颜色，如果是就取下来装填，否则去工厂里再搬一箱过来。

如果工厂里发货的顺序比较好，工人就可以顺利地完成装填。例如要按顺序装填 7 种颜色，工厂按照 7、6、1、3、2、5、4 这个顺序发货，则工人先拿到 7、6 两种不能装填的颜色，将其按照 7 在下、6 在上的顺序堆在货架上；拿到 1 时可以直接装填；拿到 3 时又得临时码放在 6 号颜色箱上；拿到 2 时可以直接装填；随后从货架顶取下 3 进行装填；然后拿到 5，临时码放到 6 上面；最后取了 4 号颜色直接装填；剩下的工作就是顺序从货架上取下 5、6、7 依次装填。

但如果工厂按照 3、1、5、4、2、6、7 这个顺序发货，工人就必须要愤怒地折腾货架了，因为装填完 2 号颜色以后，不把货架上的多个箱子搬下来就拿不到 3 号箱，就不可能顺利完成任务。

另外，货架的容量有限，如果要堆积的货物超过容量，工人也没办法顺利完成任务。例如工厂按照 7、6、5、4、3、2、1 这个顺序发货，如果货架够高，能码放 6 只箱子，那还是可以顺利完工的；但如果货架只能码放 5 只箱子，工人就又要愤怒了……

本题就请你判断一下，工厂的发货顺序能否让工人顺利完成任务。

输入格式：

输入首先在第一行给出 3 个正整数，分别是彩虹瓶的颜色数量 N（1<N≤103）、临时货架的容量 M（<N）、以及需要判断的发货顺序的数量 K。

随后 K 行，每行给出 N 个数字，是 1 到N 的一个排列，对应工厂的发货顺序。

一行中的数字都以空格分隔。

输出格式：

对每个发货顺序，如果工人可以愉快完工，就在一行中输出 YES；否则输出 NO。

输入样例：

7 5 3
7 6 1 3 2 5 4
3 1 5 4 2 6 7
7 6 5 4 3 2 1

输出样例：

YES
NO
NO

#include<stdio.h>
#include<string.h>int stack[1001] = {167890}, top = 1; // 初始化一个栈用于模拟颜色堆叠，栈顶指针top初始化为1
// 主函数
int main()
{int color_num, capacity, num, i, j; // 定义变量scanf("%d%d%d", &color_num, &capacity, &num); // 输入颜色的种类数、堆叠的最大容量和堆叠的次数int order[color_num + 1], top_order = color_num - 1; // 定义一个数组用于存储颜色堆叠顺序，初始化顶部指针为color_num-1for (i = 0; i < num; i++)  // 循环处理堆叠的次数{for (j = 0; j < color_num; j++) scanf("%d", &order[top_order--]); // 输入颜色堆叠的顺序top_order = color_num; // 重置顶部指针for (j = 1; j <= color_num;) // 根据规则进行颜色堆叠操作{if (stack[top-1] == j) {top--; j++;}else if (order[top_order-1] == j) {top_order--; j++;}else if (order[top_order-1] > stack[top-1]) break;else{stack[top++] = order[--top_order];if (top > capacity + 1) break;}}   if (j == color_num + 1) printf("YES\n"); // 输出堆叠结果else printf("NO\n"); // 输出堆叠结果memset(stack, 0, sizeof(stack)); // 清空栈top = 1; // 重置栈顶指针stack[0] = 114514; // 重新设置栈底的值memset(order, 0, sizeof(order)); // 清空堆叠顺序数组top_order = color_num - 1; // 重新设置顶部指针}return 0;
}