目录
一. 铺垫性介绍
1.1 傅里叶级数
1.2 傅里叶矩阵的来源
二. 格基与傅里叶矩阵
2.1 傅里叶矩阵详细解释
2.2 格基与傅里叶矩阵
写在前面:有关傅里叶变换的解释太多了,这篇博客主要总结傅里叶矩阵在格密码中的运用。对于有一定傅里叶变换基础的同学,可直接跳转2.2看结论。
一. 铺垫性介绍
1.1 傅里叶级数
傅里叶级数的表达如下:
傅里叶级数可以看成无限维度的线性代数。这个过程可以看成将函数f(x)投影成很多的sin与cos,与此同时产生傅里叶系数与
.
反过来,借助无限的sin与cos序列,乘以对应的傅里叶系数,也能够重建原始的函数f(x)。
当然,格密码中我们更加关心有限维度的离散傅里叶变换。
1.2 傅里叶矩阵的来源
将傅里叶级数右边的函数改为输入n个值,由此输出n个值
。这两个向量,y与c之间的关系一定是线性的,数字信号处理过程中也经常会用到此性质。既然是线性关系,那我们可以将其构建为一个矩阵,由此便出现了傅里叶矩阵F。比如,给定输出y有四个值2,4,6,8,求解输入c的本质就是:已知Fc=y,求解c,如下:
二. 格基与傅里叶矩阵
2.1 傅里叶矩阵详细解释
先从4维的离散傅里叶矩阵(后续记为DFT)F说起:
离散傅里叶矩阵的共轭矩阵记为,熟悉线性代数的都知道,DFT矩阵满足如下:

排除系数4的影响,也就是矩阵乘以本身的共轭矩阵为单位阵,这不就类似正交阵(准确来讲应该叫酉矩阵)。
给定任意的维度n,傅里叶矩阵可以将输入c与输出y联系起来。这个过程可以写成n个线性方程,当然也可以写成离散级数,包含n个傅里叶系数,n个输出点,如下:
当x取0时,也就是系数全为1,第一个线性方程往往比较简单,如下:
将1的N次方根主值记为,其实就是复数根,以上变换过程推广到n维为:

注意左边第一个矩阵即为傅里叶矩阵。将行数与列数记为从0到n-1,傅里叶矩阵中的元素可以总结为。比如第一行就是
,第一列就是
,这两个的元素均为
。
在利用傅里叶矩阵时,很多时候需要求逆。根据复数的性质,易知:
我们知道的角度为
,
的角度为
,类似如下:

也就是可以得出:
也就是傅里叶矩阵的逆长这个样子:
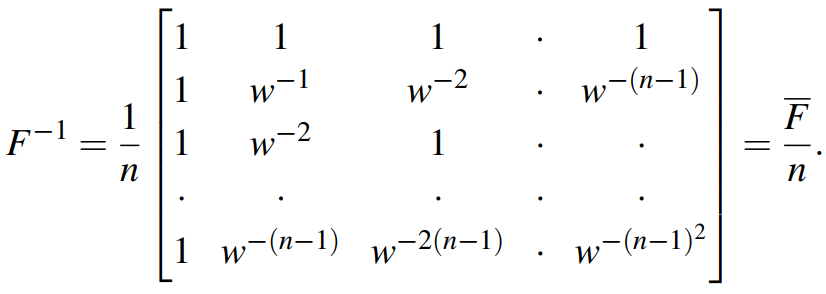
第一个等号代表,傅里叶矩阵的逆。第二个等号代表逆矩阵与共轭矩阵的关系。
如果用3维举例子的话,三维的傅里叶矩阵如下:

三维的逆傅里叶矩阵如下:

F的第j行,的第j列,相乘计算:
其实就是单位阵的对角线元素。
F的第j行乘以的第k列,计算:
除了对角线元素,其他位置均为0(单位阵)。
如果我们将,以上方程即可改写为:
因为,W满足如下:
也就是W也为1的单位根。
2.2 格基与傅里叶矩阵
格基的本质是一个矩阵,通常格点为实数的向量点。如果将其推广到复数域,格基B也可以取复数。
根据以上讨论,傅里叶矩阵:
- N维方阵;
- 对称矩阵(关于对角线);
- 正交阵(注意差N倍系数,严格叫酉矩阵);
已经出现论文讨论将傅里叶矩阵作为格基,之所以这样是有如下好处:
- 格基为正交阵,格基良好,可解决很多格上困难问题(CVP,LWE等);
- 逆矩阵容易求,很容易导出对偶格;
格密码中很多时候需要利用“环版本”,比如RLWE或者Ring-SIS问题。一个环元素本质是一个多项式,两个多项式相乘的计算复杂度为,但如果借助快速傅里叶变换(FFT),其复杂度可以降低到
。