虽然看似进入了一个新章节,但其实还是前几天二叉树章节的延续。。
回溯算法 (以下内容摘抄自代码随想录):

回溯法解决的问题都可以抽象为树形结构,是的,我指的是所有回溯法的问题都可以抽象为树形结构!
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
回溯三部曲:
- 回溯函数模板返回值以及参数
-
def backtracking(参数)
-
- 回溯函数终止条件
-
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
-
if (终止条件):存放结果return
-
- 回溯搜索的遍历过程
- 回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
-
for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
backtracking这里自己调用自己,实现递归。
大家可以从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
-
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小):处理节点;backtracking(路径,选择列表); 回溯,撤销处理结果
回溯的模版:
def backtracking(参数):if (终止条件):存放结果returnfor (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)):处理节点backtracking(路径,选择列表) # 递归回溯,撤销处理结果
77. Combinations
从n个整数里不重复挑k个,有多少种组合方式。
注意:1. 每组k不重复。2.是组合不是排列。3.此题可剪枝。
关于剪枝:第一次从n里挑k中的第一个数时,是n选1;而第二次就变成n-1选1,以此类推。极端点如果是k==n的话,其实最后一次挑选时都只有一个选择了。但还不止如此。其实如果是k==n的话一开始就应该知道只有一个选择而已,因为待选的数量==可选的数量。把递归的过程想象成树结构,如果深度<=宽度,也就是待选的数量<=可选的数量,那就直接把可选的都选了就行了,只有一种情况了。所以优化最终是要从以下这个range里选,startIndex从1开始,表示已选的数目。
range(startIndex, n - (k - len(path)) + 2)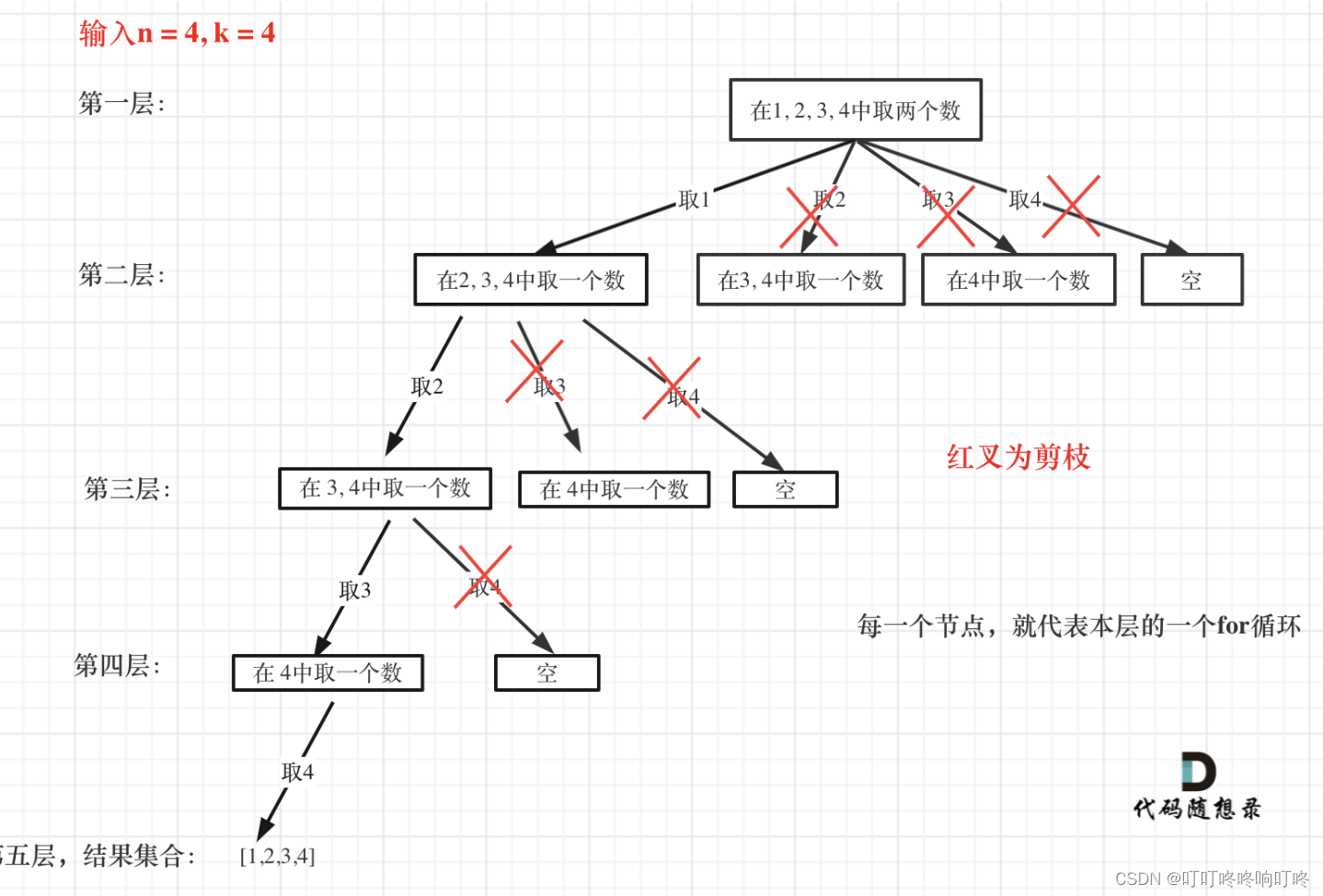
我觉得用树结构来理解递归和回溯是相对清晰容易的。结合这道题的回答来看。
self.backtracking(n, k, i + 1, path, result) #每次调用就是逐层深入
for i in range(startIndex, n - (k - len(path)) + 1): #就是遍历每一层横向的选择
回溯是为了撤销当前及更深层的选择,回复到上一层之后的样子,以进行当前层的其他选择。
关于减枝优化(from代码随想录):
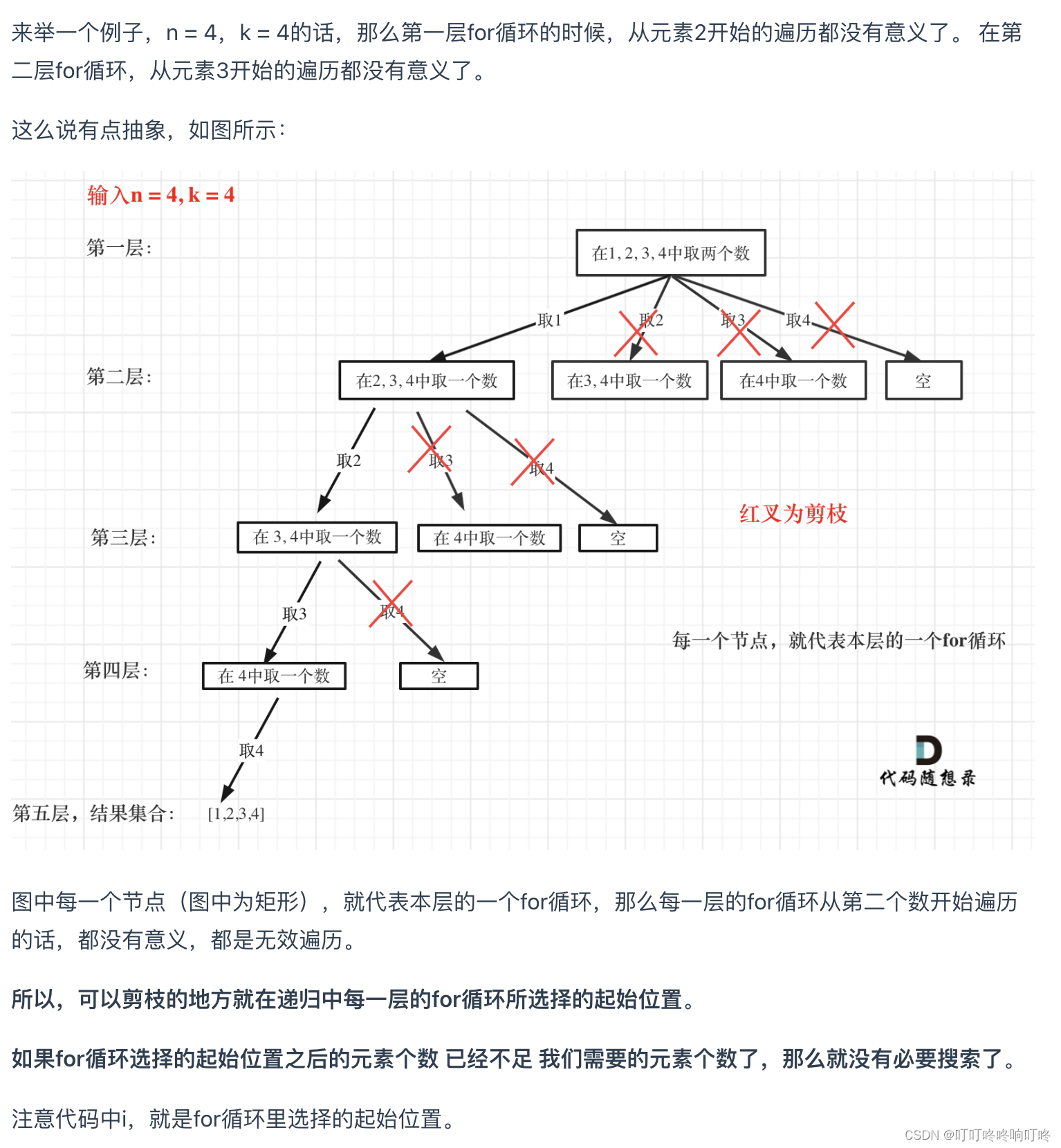

class Solution:def combine(self, n: int, k: int) -> List[List[int]]:result = [] # 存放结果集self.backtracking(n, k, 1, [], result)return resultdef backtracking(self, n, k, startIndex, path, result):if len(path) == k:result.append(path[:])returnfor i in range(startIndex, n - (k - len(path)) + 1): # 优化的地方path.append(i) # 处理节点self.backtracking(n, k, i + 1, path, result)path.pop() # 回溯,撤销处理的节点最后讨论一下算法复杂度 O(C(n, k))。因为总共就是C(n, k)种组合方式。最大的情况出现在k接近于n/2时。当我们考虑所有可能的k值时,时间复杂度会接近于2^n。也有人粗略地把这道题的算法复杂度记为:O(k * 2^n) 即每个元素都有两种选择(比如包含或不包含)的问题中,在您的问题中,但每个元素的选择不仅仅是包含或不包含,还需要考虑它们与其他元素的组合,这个算法复杂度是偏大的。
空间复杂度最大为O(k),因为会递归k层。
其实这道题也是可以用for循环来解的。需要多少个k,就来几重for循环,而且每一重的for循环元素的个数也是可以逐渐减少的,也可以实现early stop。但是如果k>100,写100多层嵌套也太笨拙了,写成递归也更方便维护。