关于“Python”的核心知识点整理大全44-编程知识

编辑

15.3.4 模拟多次随机漫步

rw_visual.py

注意

15.3.5 设置随机漫步图的样式

15.3.6 给点着色

rw_visual.py

15.3.7 重新绘制起点和终点

rw_visual.py

15.3.8 隐藏坐标轴

rw_visual.py

15.3.9 增加点数

rw_visual.py

15.3.10 调整尺寸以适合屏幕

rw_visual.py

15.4 使用 Pygal 模拟掷骰子

15.4.1 安装 Pygal

注意

15.4.2 Pygal 画廊

15.4.3 创建 Die 类

die.py

15.4.4 掷骰子

die_visual.py

15.4.5 分析结果

die_visual.py

往期快速传送门👆（在文章最后）：

感谢大家的支持！欢迎订阅收藏！专栏将持续更新！

15.3.4 模拟多次随机漫步

每次随机漫步都不同，因此探索可能生成的各种模式很有趣。要在不多次运行程序的情况下使用前面的代码模拟多次随机漫步，一种办法是将这些代码放在一个while循环中，如下所示：

rw_visual.py

import matplotlib.pyplot as plt
from random_walk import RandomWalk
# 只要程序处于活动状态，就不断地模拟随机漫步
while True:# 创建一个RandomWalk实例，并将其包含的点都绘制出来rw = RandomWalk() rw.fill_walk()plt.scatter(rw.x_values, rw.y_values, s=15)plt.show()
1 keep_running = input("Make another walk? (y/n): ")
if keep_running == 'n':break

这些代码模拟一次随机漫步，在matplotlib查看器中显示结果，再在不关闭查看器的情况下暂停。如果你关闭查看器，程序将询问你是否要再模拟一次随机漫步。如果你输入y，可模拟多次随机漫步：这些随机漫步都在起点附近进行，大多沿特定方向偏离起点，漫步点分布不均匀等。要结束程序，请输入n。

注意

如果你使用的是Python 2.7，别忘了将Ø处的input()替换为raw_input()。

15.3.5 设置随机漫步图的样式

在本节中，我们将定制图表，以突出每次漫步的重要特征，并让分散注意力的元素不那么显眼。为此，我们确定要突出的元素，如漫步的起点、终点和经过的路径。接下来确定要使其不那么显眼的元素，如刻度标记和标签。最终的结果是简单的可视化表示，清楚地指出了每次漫步经过的路径.

15.3.6 给点着色

我们将使用颜色映射来指出漫步中各点的先后顺序，并删除每个点的黑色轮廓，让它们的颜色更明显。为根据漫步中各点的先后顺序进行着色，我们传递参数c，并将其设置为一个列表，其中包含各点的先后顺序。由于这些点是按顺序绘制的，因此给参数c指定的列表只需包含数字 1~5000，如下所示：

rw_visual.py

--snip--
while True:# 创建一个RandomWalk实例，并将其包含的点都绘制出来rw = RandomWalk()rw.fill_walk()
1 point_numbers = list(range(rw.num_points))
plt.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues,edgecolor='none', s=15)plt.show()keep_running = input("Make another walk? (y/n): ")--snip--

在1处，我们使用了range()生成了一个数字列表，其中包含的数字个数与漫步包含的点数相同。接下来，我们将这个列表存储在point_numbers中，以便后面使用它来设置每个漫步点的颜色。我们将参数c设置为point_numbers，指定使用颜色映射Blues，并传递实参edgecolor=none以删除每个点周围的轮廓。最终的随机漫步图从浅蓝色渐变为深蓝色，如图15-9所示。

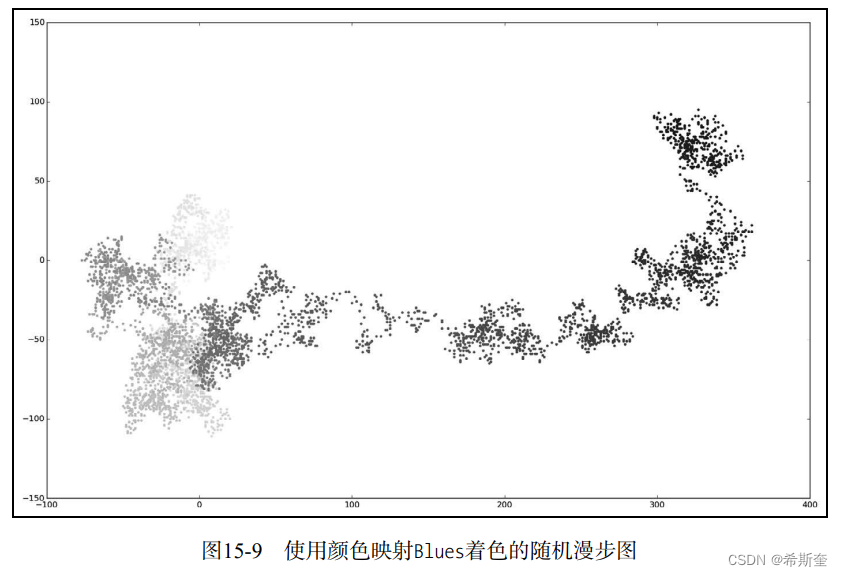
15.3.7 重新绘制起点和终点

除了给随机漫步的各个点着色，以指出它们的先后顺序外，如果还能呈现随机漫步的起点和终点就更好了。为此，可在绘制随机漫步图后重新绘制起点和终点。我们让起点和终点变得更大，并显示为不同的颜色，以突出它们，如下所示：

rw_visual.py

--snip--
while True:--snip--plt.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues,edgecolor='none', s=15)# 突出起点和终点plt.scatter(0, 0, c='green', edgecolors='none', s=100)plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none',s=100)plt.show()--snip--

为突出起点，我们使用绿色绘制点(0, 0)，并使其比其他点大（s=100）。为突出终点，我们在漫步包含的最后一个x和y值处绘制一个点，将其颜色设置为红色，并将尺寸设置为100。请务必将这些代码放在调用plt.show()的代码前面，确保在其他点的上面绘制起点和终点。如果你现在运行这些代码，将能准确地知道每次随机漫步的起点和终点（如果起点和终点不明显，请调整它们的颜色和大小，直到明显为止）。

15.3.8 隐藏坐标轴

下面来隐藏这个图表中的坐标轴，以免我们注意的是坐标轴而不是随机漫步路径。要隐藏坐标轴，可使用如下代码：

rw_visual.py

--snip--
while True:--snip--plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none',s=100)# 隐藏坐标轴
1 plt.axes().get_xaxis().set_visible(False)
plt.axes().get_yaxis().set_visible(False)plt.show()--snip--

为修改坐标轴，使用了函数plt.axes()（见Ø）来将每条坐标轴的可见性都设置为False。随着你越来越多地进行数据可视化，经常会看到这种串接方法的方式。如果你现在运行rw_visual.py，将看到一系列图形，但看不到坐标轴。

15.3.9 增加点数

下面来增加点数，以提供更多的数据。为此，我们在创建RandomWalk实例时增大num_points 的值，并在绘图时调整每个点的大小，如下所示：

rw_visual.py

--snip--
while True:#创建一个RandomWalk实例，并将其包含的点都绘制出来rw = RandomWalk(50000)rw.fill_walk()# 绘制点并将图形显示出来point_numbers = list(range(rw.num_points)) plt.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues,edgecolor='none', s=1)--snip--

这个示例模拟了一次包含50 000个点的随机漫步（以模拟现实情况），并将每个点的大小都设置为1。最终的随机漫步图更纤细，犹如云朵，如图15-10所示。正如你看到的，我们使用简单的散点图制作出了一件艺术品！

请尝试修改上述代码，看看将漫步包含的点数增加到多少后，程序的运行速度变得极其缓慢或绘制出的图形变得很难看。

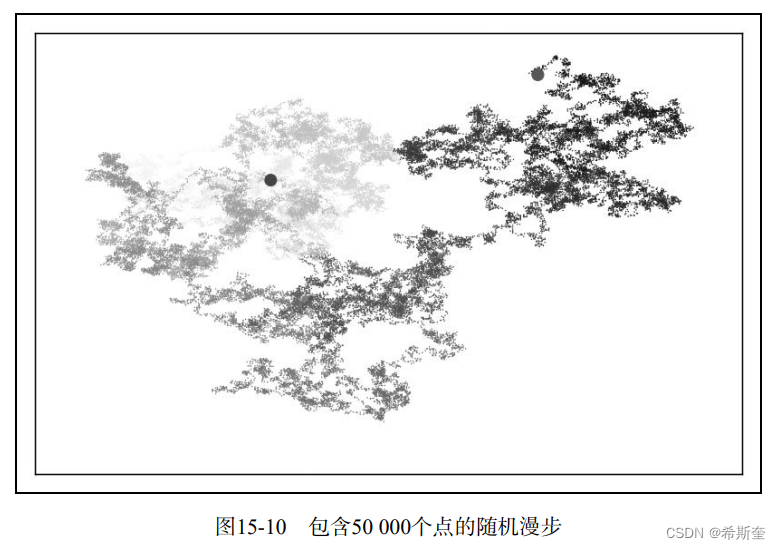
15.3.10 调整尺寸以适合屏幕

图表适合屏幕大小时，更能有效地将数据中的规律呈现出来。为让绘图窗口更适合屏幕大小，可像下面这样调整matplotlib输出的尺寸：

rw_visual.py

--snip--
while True:# 创建一个RandomWalk实例，并将其包含的点都绘制出来rw = RandomWalk()rw.fill_walk()# 设置绘图窗口的尺寸plt.figure(figsize=(10, 6))--snip--

函数figure()用于指定图表的宽度、高度、分辨率和背景色。你需要给形参figsize指定一个元组，向matplotlib指出绘图窗口的尺寸，单位为英寸。

Python假定屏幕分辨率为80像素/英寸，如果上述代码指定的图表尺寸不合适，可根据需要调整其中的数字。如果你知道自己的系统的分辨率，可使用形参dpi向figure()传递该分辨率，以有效地利用可用的屏幕空间，如下所示：

plt.figure(dpi=128, figsize=(10, 6))

15.4 使用 Pygal 模拟掷骰子

在本节中，我们将使用Python可视化包Pygal来生成可缩放的矢量图形文件。对于需要在尺寸不同的屏幕上显示的图表，这很有用，因为它们将自动缩放，以适合观看者的屏幕。如果你打算以在线方式使用图表，请考虑使用Pygal来生成它们，这样它们在任何设备上显示时都会很美观。

在这个项目中，我们将对掷骰子的结果进行分析。掷6面的常规骰子时，可能出现的结果为 1~6点，且出现每种结果的可能性相同。然而，如果同时掷两个骰子，某些点数出现的可能性将比其他点数大。为确定哪些点数出现的可能性最大，我们将生成一个表示掷骰子结果的数据集，并根据结果绘制出一个图形。在数学领域，常常利用掷骰子来解释各种数据分析，但它在赌场和其他博弈场景中也得到了实际应用，在游戏《大富翁》以及众多角色扮演游戏中亦如此。

15.4.1 安装 Pygal

请使用pip来安装Pygal（如果还未使用过pip，请参阅12.2.1节）。在Linux和OS X系统中，应执行的命令类似于下面这样：

pip install --user pygal

在Windows系统中，命令类似于下面这样：

python -m pip install --user pygal

注意

你可能需要使用命令pip3而不是pip，如果这还是不管用，你可能需要删除标志--user。

15.4.2 Pygal 画廊

要了解使用Pygal可创建什么样的图表，请查看图表类型画廊：访问http://www.pygal.org/，单击Documentation，再单击Chart types。每个示例都包含源代码，让你知道这些图表是如何生成的。

15.4.3 创建 Die 类

下面的类模拟掷一个骰子：

die.py

from random import randint
class Die():"""表示一个骰子的类"""
1 def __init__(self, num_sides=6):"""骰子默认为6面"""self.num_sides = num_sidesdef roll(self):""""返回一个位于1和骰子面数之间的随机值"""
2 return randint(1, self.num_sides)

方法__init__()接受一个可选参数。创建这个类的实例时，如果没有指定任何实参，面数默认为6；如果指定了实参，这个值将用于设置骰子的面数（见1）。骰子是根据面数命名的，6面的骰子名为D6，8面的骰子名为D8，以此类推。

方法roll()使用函数randint()来返回一个1和面数之间的随机数（见2）。这个函数可能返回起始值1、终止值num_sides或这两个值之间的任何整数。

15.4.4 掷骰子

使用这个类来创建图表前，先来掷D6骰子，将结果打印出来，并检查结果是否合理：

die_visual.py

from die import Die
# 创建一个D6
1 die = Die()
# 掷几次骰子，并将结果存储在一个列表中
results = []
2 for roll_num in range(100):result = die.roll()results.append(result)
print(results)

在1处，我们创建了一个Die实例，其面数为默认值6。在2处，我们掷骰子100次，并将每次的结果都存储在列表results中。下面是一个示例结果集：

[4, 6, 5, 6, 1, 5, 6, 3, 5, 3, 5, 3, 2, 2, 1, 3, 1, 5, 3, 6, 3, 6, 5, 4,1, 1, 4, 2, 3, 6, 4, 2, 6, 4, 1, 3, 2, 5, 6, 3, 6, 2, 1, 1, 3, 4, 1, 4,3, 5, 1, 4, 5, 5, 2, 3, 3, 1, 2, 3, 5, 6, 2, 5, 6, 1, 3, 2, 1, 1, 1, 6,5, 5, 2, 2, 6, 4, 1, 4, 5, 1, 1, 1, 4, 5, 3, 3, 1, 3, 5, 4, 5, 6, 5, 4,1, 5, 1, 2]

通过快速扫描这些结果可知，Die类看起来没有问题。我们见到了值1和6，这表明返回了最大和最小的可能值；我们没有见到0或7，这表明结果都在正确的范围内。我们还看到了1~6的所有数字，这表明所有可能的结果都出现了。

15.4.5 分析结果

为分析掷一个D6骰子的结果，我们计算每个点数出现的次数：

die_visual.py

--snip--
# 掷几次骰子，并将结果存储在一个列表中
results = []
1 for roll_num in range(1000):result = die.roll()results.append(result)
# 分析结果
frequencies = []
2 for value in range(1, die.num_sides+1):
3 frequency = results.count(value)
4 frequencies.append(frequency)
print(frequencies)

由于我们将使用Pygal来进行分析，而不是将结果打印出来，因此可以将模拟掷骰子的次数增加到1000（见1）。为分析结果，我们创建空列表frequencies，用于存储每种点数出现的次数。在2处，我们遍历可能的点数（这里为1~6），计算每种点数在results中出现了多少次（见3），并将这个值附加到列表frequencies的末尾（见4）。接下来，我们在可视化之前将这个列表打印出来：