【图像分类】【深度学习】【轻量级网络】【Pytorch版本】ShuffleNet_V2模型算法详解
文章目录
- 【图像分类】【深度学习】【轻量级网络】【Pytorch版本】ShuffleNet_V2模型算法详解
- 前言
- ShuffleNet_V2讲解
- 四条实用指导思想
- G1:相等的通道宽度可以降低存储访问成本
- G2:大量的分组卷积数量会增加存储访问
- G3:网络碎片化会降低并行度
- G4:元素级操作是不可忽略的
- ShuffleNet_V2的模型结构
- ShuffleNet_V2 Pytorch代码
- 完整代码
- 总结
前言
ShuffleNet_V2是由旷视科技的Ma, Ningning等人在《ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design【ECCV-2018】》【论文地址】一文中提出的改进模型,论文中提出了高效网络架构设计的两大原则:第一,使用直接指标(如速度)而非间接指标(如FLOPs);第二,提出了四条与跨平台的设计指南,并在该指南指导下设计了ShuffleNet_V2。
ShuffleNet_V2讲解
过去的一些网络模型如MobileNet_v1, v2,ShuffleNet_v1, Xception采用了分组卷积或深度可分离卷积等操作在一定程度上减少了浮点数运算量(float-point operations,FLOPs),但FLOPs并不是一个直接衡量模型速度的指标,它只是通过理论上的计算量来间接衡量模型的速度。
然而在实际设备上,由于各种各样的优化计算操作,它还会受到内存访问消耗(memory access cost,MAC)和平台特点的限制,导致计算量并不能准确地衡量模型的速度,换言之,相同的FLOPs出现了不同的推理速度。下图是原论文中不同的情况下,推理速度的具体情况: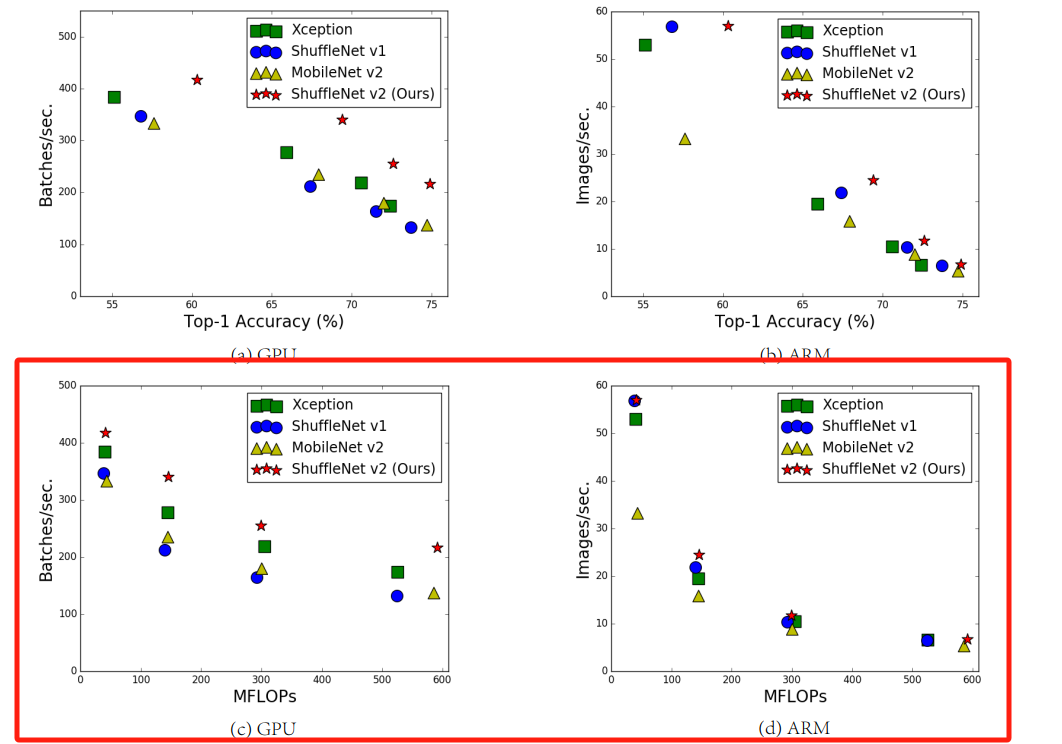
速度不完全由FLOPs决定: 如上图所示,红色框内表示不同样设备,左侧为GPU上结果,右侧为ARM上的结果。从下面两幅图可以看出,当不同模型MFLOPs相同时,速度却不同。
Batches/sec:数据仓库每秒写入操作模块接收的批数。
那么还有什么因素会影响设备上运行的速度呢?论文给出了解释,即直接指标与间接指标的矛盾可以归咎于两点原因。
- 第一,FLOPs没有考虑影响速度的一些重要因素。例如内存访问成本,它在group
convolution中占据大量运算时间,也是GPU运算时的潜在性能瓶颈;还有并行度,相同FLOPs的情况下,高度并行的网络执行起来会更加迅速。 - 第二,FLOPs相同的操作,在不同平台下运行时不同。例如早期工作广泛使用张量分解来加速矩阵乘法虽然它可以减少75%的FLOPs,但是在GPU上运算却更慢了,这是因为CuDnn针对3×3卷积做了特殊优化,3×3卷积不再是1×1卷积理论上的9倍耗时,这种分解来加速没有明显的意义了。
因此,论文提出了高效网络架构设计的两大原则。第一,使用直接指标(如速度)而非间接指标(如FLOPs);第二,需要在目标平台上验证该指标,同时提出了四条与跨平台的设计指南,并在该指南指导下设计了一款新的网络架构ShuffleNet V2。
四条实用指导思想
下图是原论文关于ShuffleNet_V1和MobileNet _V2网络组件运行速度统计:
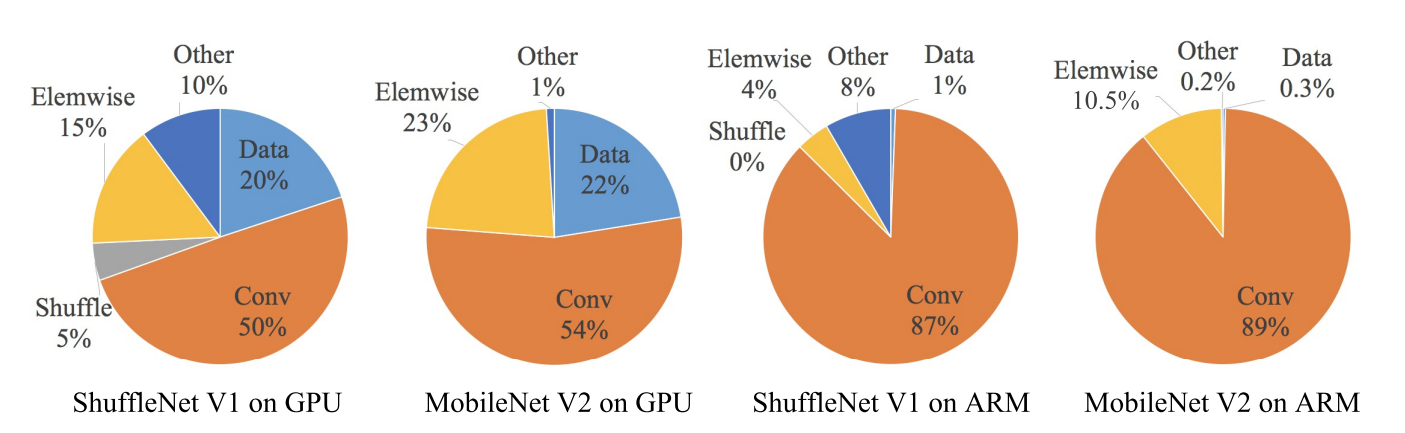
从图中可以看到模型在GPU/ARM上各项操作所花费的时间,FLOPs仅表示了卷积部分的计算量,占据了总运行时间的绝大部分,而实际上Elemwise、Data相关部分也耗费相当大的时间,包括数据输入输出,数据打乱,元素级处理相关操作(张量相加,激活函数处理等)。
在特定的平台下研究ShuffleNetv1和MobileNetv2的运行时间,并结合理论与实验,论文提出了四条实用的指导原则。
G1:相等的通道宽度可以降低存储访问成本
Equal channel width minimizes memory access cost (MAC)
现在的网络如Xception【参考】, MobileNet_V1【参考】, MobileNet_V2【参考】, ShuffleNet_V1【参考】都采用了深度可分离卷积,1×1点卷积占据了大部分的计算复杂度:假设输入特征图为 h × w × c 1 {\rm{h}} \times {\rm{w}} \times {{\rm{c}}_1} h×w×c1,1×1点卷积为 c 1 × c 2 × 1 × 1 {{\rm{c}}_1} \times {{\rm{c}}_2} \times 1 \times 1 c1×c2×1×1,输出特征图尺寸不变,那么1×1点卷积的FLOPs为 B = h × w × c 1 × c 2 {\rm{B = h}} \times {\rm{w}} \times {{\rm{c}}_1} \times {{\rm{c}}_2} B=h×w×c1×c2。
FLOPs计算是把乘加当作一次浮点运算
假设计算设备的缓冲足够大能够存放下整个特征图和所有参数,1×1点卷积的内存访问代价(内存访问次数)为 M A C = h w c 1 + h w c 2 + c 1 c 2 = h w ( c 1 + c 2 ) + c 1 c 2 {\rm{MAC = hw}}{{\rm{c}}_1}{\rm{ + hw}}{{\rm{c}}_2} + {{\rm{c}}_1}{{\rm{c}}_2} = {\rm{hw(}}{{\rm{c}}_1}{\rm{ + }}{{\rm{c}}_2}) + {{\rm{c}}_1}{{\rm{c}}_2} MAC=hwc1+hwc2+c1c2=hw(c1+c2)+c1c2,即代表输入特征图、输出特征图和权重参数的代价。
当固定 B B B时, c 2 = B h w c 1 {{\rm{c}}_2} = \frac{B}{{hw{{\rm{c}}_1}}} c2=hwc1B,根据均值不等式
M A C = h w ( c 1 + c 2 ) + c 1 c 2 = ( h w ) 2 ( c 1 + c 2 ) 2 + B h w ≥ ( h w ) 2 ( 4 c 1 c 2 ) + B h w ≥ 2 h w B + B h w {\rm{MAC = hw(}}{{\rm{c}}_1}{\rm{ + }}{{\rm{c}}_2}) + {{\rm{c}}_1}{{\rm{c}}_2} = \sqrt {{{{\rm{(hw}})}^2}{{{\rm{(}}{{\rm{c}}_1}{\rm{ + }}{{\rm{c}}_2})}^2}} + \frac{B}{{hw}} \ge \sqrt {{{{\rm{(hw}})}^2}{\rm{(4}}{{\rm{c}}_1}{{\rm{c}}_2})} + \frac{B}{{hw}} \ge 2\sqrt {{\rm{hwB}}} + \frac{B}{{hw}} MAC=hw(c1+c2)+c1c2=(hw)2(c1+c2)2+hwB≥(hw)2(4c1c2)+hwB≥2hwB+hwB
由均值不等式,可知当 c 1 = c 2 {{\rm{c}}_1} = {{\rm{c}}_2} c1=c2时取 ( c 1 + c 2 ) 2 {{\rm{(}}{{\rm{c}}_1}{\rm{ + }}{{\rm{c}}_2})^2} (c1+c2)2的下限,即 ( c 1 + c 2 ) 2 = 4 c 1 c 2 {{\rm{(}}{{\rm{c}}_1}{\rm{ + }}{{\rm{c}}_2})^2} = {\rm{4}}{{\rm{c}}_1}{{\rm{c}}_2} (c1+c2)2=4c1c2, M A C MAC MAC取得最小值。
在给定计算量的限制情况下, M A C MAC MAC是有下界的。
为了验证这个结论,论文进行了实验分析,下表中测试网络由10个重复块堆叠而成,其中每个块包含两个卷积层,输入通道是 c 1 {{\rm{c}}_1} c1 ,输出通道是 c 2 {{\rm{c}}_2} c2。
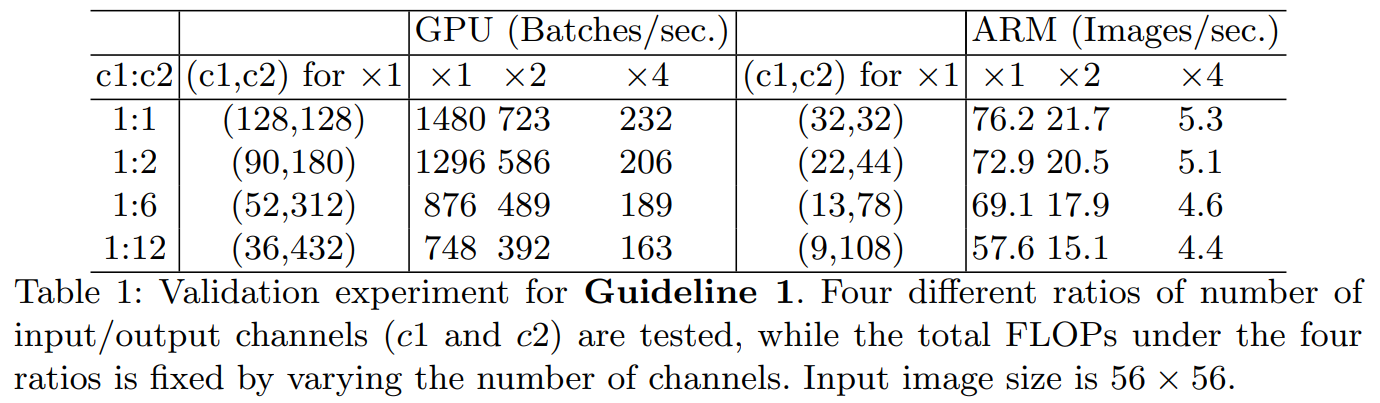
从表中的数据可以得到:当 c 1 : c 2 {{\rm{c}}_1}{\rm{:}}{{\rm{c}}_2} c1:c2值接近 1:1的时候,MAC值越来越小,网络运行的评估速度是越来越快的。
G2:大量的分组卷积数量会增加存储访问
Excessive group convolution increases MAC
分组卷积是现在网络结构设计的核心,它通过通道之间的稀疏连接,也就是只和同一个组内的特征连接来降低计算复杂度FLOPs。一方面,它允许使用更多的通道数来增加网络容量进而提升准确率,但另一方面随着通道数的增多也对带来更多的MAC。
针对1×1的分组卷积,分组卷积FLOPs的计算公式:
B = h × w × 1 × 1 × c 1 g × c 2 g × g = h w c 1 c 2 g {\rm{B = h}} \times {\rm{w}} \times 1 \times 1 \times \frac{{{{\rm{c}}_1}}}{g} \times \frac{{{{\rm{c}}_2}}}{g} \times g = \frac{{{\rm{hw}}{{\rm{c}}_1}{{\rm{c}}_2}}}{g} B=h×w×1×1×gc1×gc2×g=ghwc1c2
分组卷积MAC的计算公式:
M A C = h w ( c 1 + c 2 ) + c 1 c 2 g = h w c 1 + B g c 1 + B h w MAC = hw({c_1} + {c_2}) + \frac{{{c_1}{c_2}}}{g} = hw{c_1} + \frac{{Bg}}{{{c_1}}} + \frac{B}{{hw}} MAC=hw(c1+c2)+gc1c2=hwc1+c1Bg+hwB
输入特征图 h × w × c 1 {\rm{h}} \times {\rm{w}} \times {{\rm{c}}_1} h×w×c1是固定的,当固定 B B B时就需要固定 c 2 g \frac{{{c_2}}}{g} gc2的比值,所以 M A C MAC MAC与 g g g成正比的关系。
论文通过叠加10个分组点卷积层设计了实验,在保证计算代价FLOPs相同的情况下采用不同的分组组数测试模型的运行时间,结果如下表所示。

在总计算量固定的情况下,改变分组的数量,可以看到使用分组数量越多,实际运行速度越慢。因此论文建议要根据硬件平台和目标任务谨慎地选择分组卷积的组数,不能简单地因为可以提升准确率就选择很大的组数,而忽视了内存访问代价MAC的增加。
G3:网络碎片化会降低并行度
Network fragmentation reduces degree of parallelism
在GoogLeNet系列:Inception V1【参考】,V2【参考】,V3【参考】V4【参考】等网路中每个单元块使用了多分支结构(multi-path),,这种结构中多采用小算子(fragmented operators 支路算子/碎片算子)而不是大算子,网络结构块block中的每一个卷积或者池化操作称之为一个小算子fragmented operator。过去的论文已经表明,支路结构(fragmented structure)能够提升模型的准确性,但是其会降低效率,因为这种结构 GPU 对并行性强的设备不友好。
为了量化网络碎片化(network fragmentation),即网络分支如何影响效率,论文评估了一系列具有不同碎片化程度(degree of fragmentation)的网络结构块。

具体来说,对比实验实验的每个构建块由1到4个顺序或者并行结构的1x1卷积层组成。
为了验证网络分支对性能的影响,论文进行了不同分支程度网络的对比实验。每个块重复堆叠10次。下表结果表明碎片化会降低 GPU 的速度。

过多的网络分支在GPU设备上会大幅度降低运行速度,但在ARM平台上速度降低的相对平缓。
G4:元素级操作是不可忽略的
Element-wise operations are non-negligible
一些元素级的操作(element-wise operator)同样占据了相当的一部分时间,尤其是在GPU设备上。虽然FLOPs相对较小,但是MAC值却很大。特别地,论文推断深度卷积也是元素级操作,通常有较高的MAC/FLOPs的值。
论文中逐元素算子(元素级的操作)包括 ReLU、AddTensor、AddBias 等
论文使用 ResNet 的 “bottleneck” 单元进行实验,在实验中删除了ReLU和shortcut操作,在GPU和ARM设备上,运行速度大约提升了约20%,结果如下表所示。
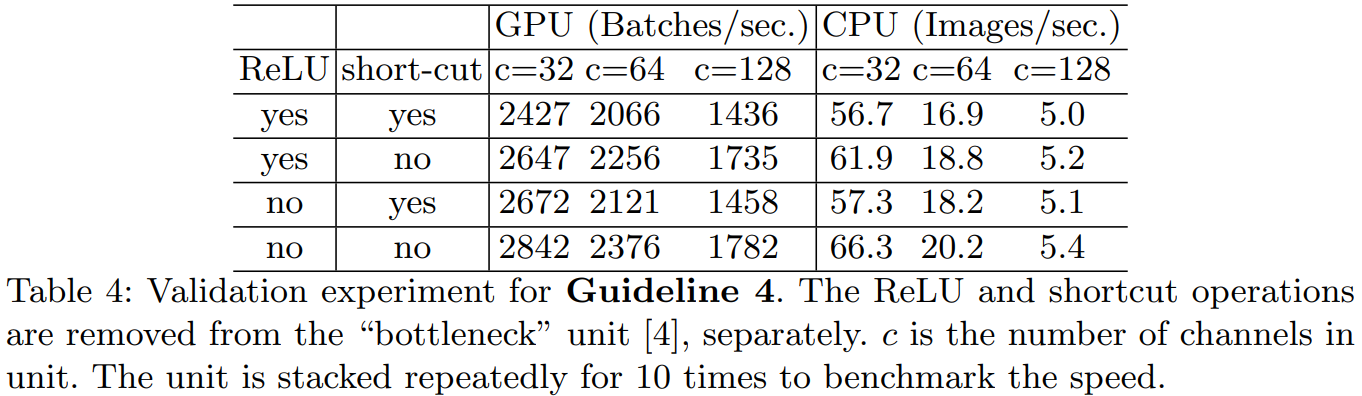
ShuffleNet_V2的模型结构
ShuffleNet_V1采用了两种技术:逐点组卷积和类瓶颈结构。从本文上个章节介绍中可以得知逐点组卷积和瓶颈结构都增加了MAC(G2原则和G1原则),尤其是对于轻量级网络来说是不能忽略的。另外,使用分组太多和残差连接中的逐元素加法也不可取 (G3原则和G4原则)。
所以要构建一个高效的网络模型,关键是如何保持大量且同样宽的通道,不能有太多的密集卷积数量和分组数量。因此在ShuffleNet_V1基本单元的基础上,ShuffleNet_V2基本单元引入通道分割(Channel Split)。
下图是原论文中ShuffleNet_V1和ShuffleNet_V2的对比示意图:
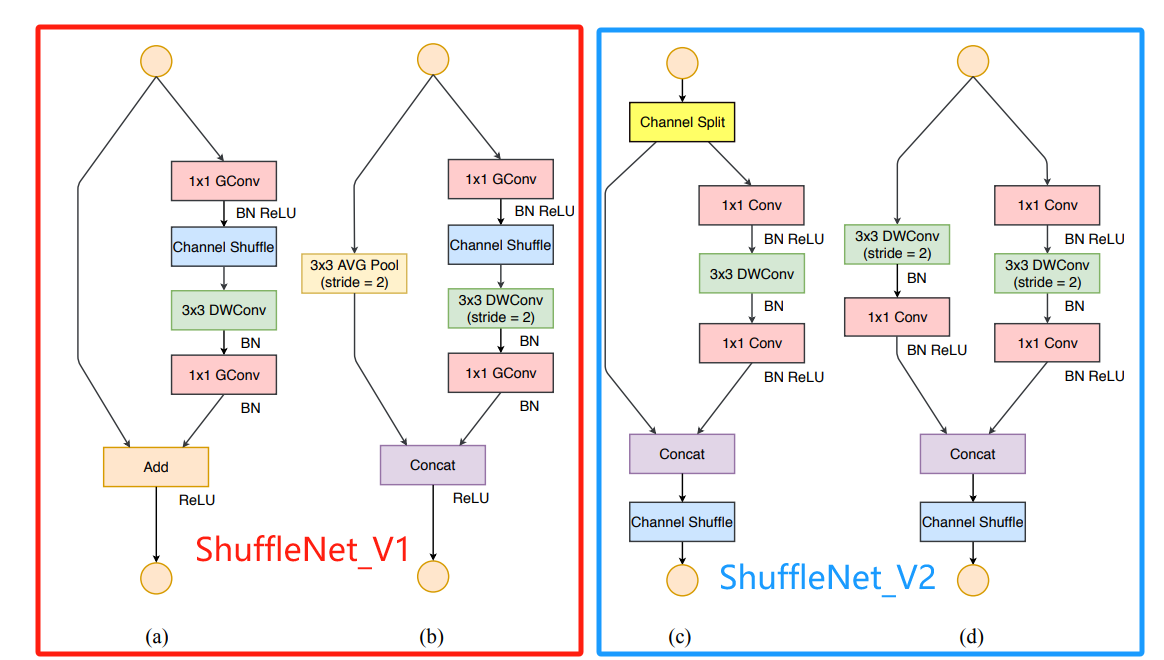
在stride=1时,ShuffleNet_V2的基本单元通过通道切分将输入 c c c个通道特征图切分成两个分支部分:一部分是 c , {{\rm{c}}^,} c,个通道的捷径分支,另一部分是 c − c , {\rm{c - }}{{\rm{c}}^,} c−c,个通道的主干分支,简单起见设置 c , = c / 2 {{\rm{c}}^,} = c/2 c,=c/2 (满足G3原则),通道切分操作也变相完成了分组效果,一半的特征图绕过当前基本单元直接进入下个基本单元,类似于DenseNet【参考】。主干分支包含三个通道数相同的卷积 (满足G1原则);并且两个1×1卷积不再使用ShuffleNet_V1时的分组卷积,而是变成了原来普通的卷积 (满足G2原则),因此主干分支的通道混洗移到拼接之后了。最后对两个分支的输出进行拼接,而不再是ShuffleNet_V1中的相加,保持基本单元输入输出通道数一致 (满足G1原则)。
在stride=2时,通道切分被移除,将ShuffleNet_V1捷径分支上的3x3平均池化替换成通过3x3深度卷积+1x1普通卷积的组合。
逐元素操作算子ReLU只存在于在右边的分支,并将三个连续的逐元素操作算子:拼接、通道混洗和通道拆分合并成一个逐元素算子 (满足G4原则)。
下图是原论文给出的关于ShuffleNet_V2模型结构的详细示意图:

ShuffleNet_V2在图像分类中分为两部分:backbone部分: 主要由ShuffleNet_V2基本单元、卷积层和池化层(汇聚层)组成,分类器部分:由全局池化层和全连接层组成 。
ShuffleNet_V2的基本单元通道数是按照0.5x等比例进行缩放,以生成不同复杂度的ShuffleNet_V2网络。
ShuffleNet_V2 Pytorch代码
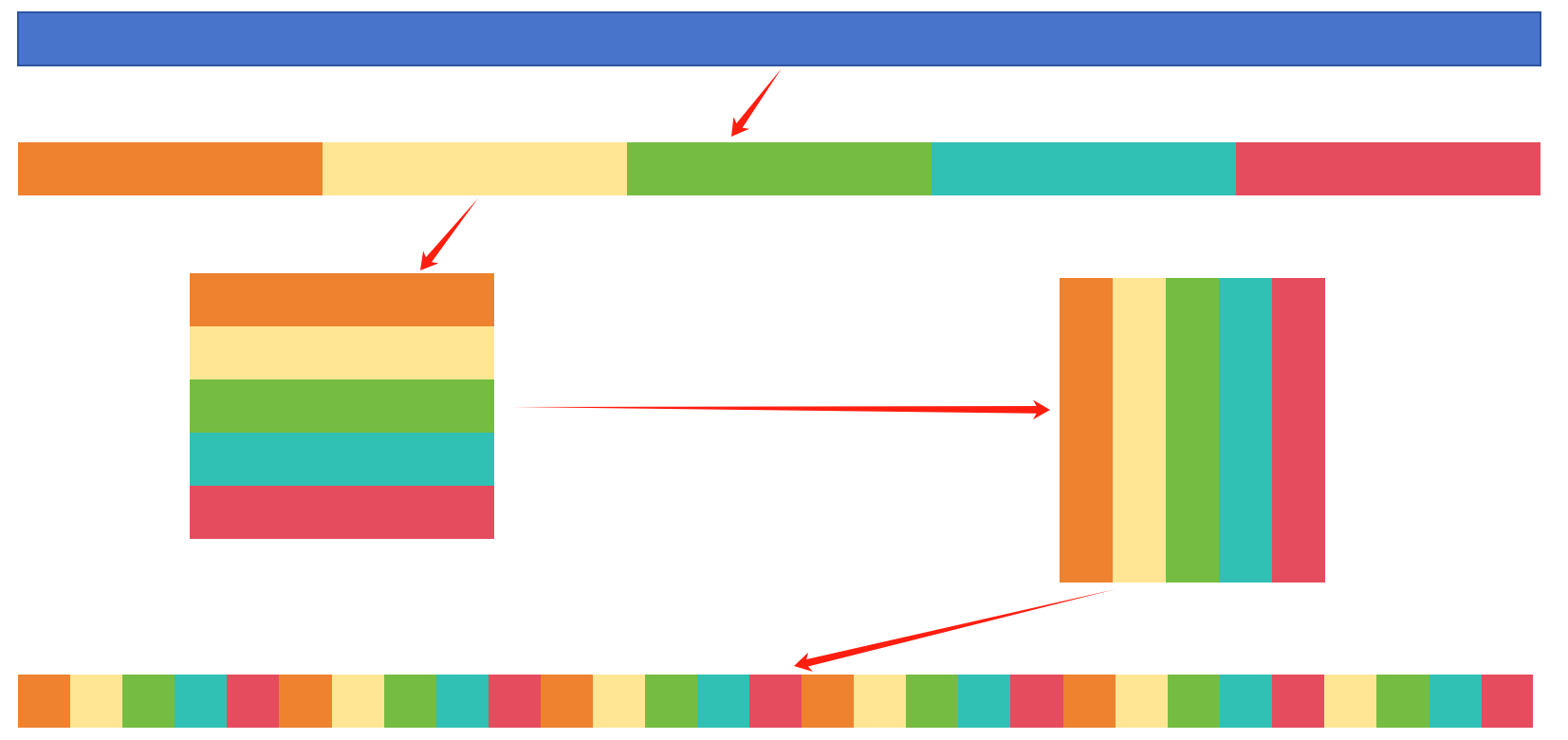
通道混洗: 更强的特征交互性和表达能力。
def channel_shuffle(x, groups):# 获得特征图的所以维度的数据batch_size, num_channels, height, width = x.shape# 对特征通道进行分组channels_per_group = num_channels // groups# reshape新增特征图的维度x = x.view(batch_size, groups, channels_per_group, height, width)# 通道混洗(将输入张量的指定维度进行交换)x = torch.transpose(x, 1, 2).contiguous()# reshape降低特征图的维度x = x.view(batch_size, -1, height, width)return x
通道混洗的代码示意图如下图所示:
ShuffleNet Uint基础单元): 1×1卷积和3×3深度卷积+BN层+激活函数
class ShuffleUnit(nn.Module):def __init__(self, input_c: int, output_c: int, stride: int):super(ShuffleUnit, self).__init__()# 步长必须在1和2之间if stride not in [1, 2]:raise ValueError("illegal stride value.")self.stride = stride# 输出通道必须能二被等分assert output_c % 2 == 0branch_features = output_c // 2# 当stride为1时,input_channel是branch_features的两倍# '<<' 是位运算,可理解为计算×2的快速方法assert (self.stride != 1) or (input_c == branch_features << 1)# 捷径分支if self.stride == 2:# 进行下采样:3×3深度卷积+1×1卷积self.branch1 = nn.Sequential(self.depthwise_conv(input_c, input_c, kernel_s=3, stride=self.stride, padding=1),nn.BatchNorm2d(input_c),nn.Conv2d(input_c, branch_features, kernel_size=1, stride=1, padding=0, bias=False),nn.BatchNorm2d(branch_features),nn.ReLU(inplace=True))else:# 不进行下采样:保持原状self.branch1 = nn.Sequential()# 主干分支self.branch2 = nn.Sequential(# 1×1卷积+3×3深度卷积+1×1卷积nn.Conv2d(input_c if self.stride > 1 else branch_features, branch_features, kernel_size=1,stride=1, padding=0, bias=False),nn.BatchNorm2d(branch_features),nn.ReLU(inplace=True),self.depthwise_conv(branch_features, branch_features, kernel_s=3, stride=self.stride, padding=1),nn.BatchNorm2d(branch_features),nn.Conv2d(branch_features, branch_features, kernel_size=1, stride=1, padding=0, bias=False),nn.BatchNorm2d(branch_features),nn.ReLU(inplace=True))# 深度卷积@staticmethoddef depthwise_conv(input_c, output_c, kernel_s, stride, padding, bias= False):return nn.Conv2d(in_channels=input_c, out_channels=output_c, kernel_size=kernel_s,stride=stride, padding=padding, bias=bias, groups=input_c)def forward(self, x):if self.stride == 1:# 通道切分x1, x2 = x.chunk(2, dim=1)# 主干分支和捷径分支拼接out = torch.cat((x1, self.branch2(x2)), dim=1)else:# 通道切分被移除# 主干分支和捷径分支拼接out = torch.cat((self.branch1(x), self.branch2(x)), dim=1)# 通道混洗out = channel_shuffle(out, 2)return out
完整代码
from typing import List, Callableimport torch
from torch import Tensor
import torch.nn as nn
from torchsummary import summarydef channel_shuffle(x, groups):# 获得特征图的所以维度的数据batch_size, num_channels, height, width = x.shape# 对特征通道进行分组channels_per_group = num_channels // groups# reshape新增特征图的维度x = x.view(batch_size, groups, channels_per_group, height, width)# 通道混洗(将输入张量的指定维度进行交换)x = torch.transpose(x, 1, 2).contiguous()# reshape降低特征图的维度x = x.view(batch_size, -1, height, width)return xclass ShuffleUnit(nn.Module):def __init__(self, input_c: int, output_c: int, stride: int):super(ShuffleUnit, self).__init__()# 步长必须在1和2之间if stride not in [1, 2]:raise ValueError("illegal stride value.")self.stride = stride# 输出通道必须能二被等分assert output_c % 2 == 0branch_features = output_c // 2# 当stride为1时,input_channel是branch_features的两倍# '<<' 是位运算,可理解为计算×2的快速方法assert (self.stride != 1) or (input_c == branch_features << 1)# 捷径分支if self.stride == 2:# 进行下采样:3×3深度卷积+1×1卷积self.branch1 = nn.Sequential(self.depthwise_conv(input_c, input_c, kernel_s=3, stride=self.stride, padding=1),nn.BatchNorm2d(input_c),nn.Conv2d(input_c, branch_features, kernel_size=1, stride=1, padding=0, bias=False),nn.BatchNorm2d(branch_features),nn.ReLU(inplace=True))else:# 不进行下采样:保持原状self.branch1 = nn.Sequential()# 主干分支self.branch2 = nn.Sequential(# 1×1卷积+3×3深度卷积+1×1卷积nn.Conv2d(input_c if self.stride > 1 else branch_features, branch_features, kernel_size=1,stride=1, padding=0, bias=False),nn.BatchNorm2d(branch_features),nn.ReLU(inplace=True),self.depthwise_conv(branch_features, branch_features, kernel_s=3, stride=self.stride, padding=1),nn.BatchNorm2d(branch_features),nn.Conv2d(branch_features, branch_features, kernel_size=1, stride=1, padding=0, bias=False),nn.BatchNorm2d(branch_features),nn.ReLU(inplace=True))# 深度卷积@staticmethoddef depthwise_conv(input_c, output_c, kernel_s, stride, padding, bias= False):return nn.Conv2d(in_channels=input_c, out_channels=output_c, kernel_size=kernel_s,stride=stride, padding=padding, bias=bias, groups=input_c)def forward(self, x):if self.stride == 1:# 通道切分x1, x2 = x.chunk(2, dim=1)# 主干分支和捷径分支拼接out = torch.cat((x1, self.branch2(x2)), dim=1)else:# 通道切分被移除# 主干分支和捷径分支拼接out = torch.cat((self.branch1(x), self.branch2(x)), dim=1)# 通道混洗out = channel_shuffle(out, 2)return outclass ShuffleNetV2(nn.Module):def __init__(self, stages_repeats, stages_out_channels, num_classes=1000, ShuffleUnit=ShuffleUnit):super(ShuffleNetV2, self).__init__()if len(stages_repeats) != 3:raise ValueError("expected stages_repeats as list of 3 positive ints")if len(stages_out_channels) != 5:raise ValueError("expected stages_out_channels as list of 5 positive ints")self._stage_out_channels = stages_out_channels# 输入通道input_channels = 3output_channels = self._stage_out_channels[0]self.conv1 = nn.Sequential(nn.Conv2d(input_channels, output_channels, kernel_size=3, stride=2, padding=1, bias=False),nn.BatchNorm2d(output_channels),nn.ReLU(inplace=True))input_channels = output_channelsself.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)# 三个基本单元组层self.stage2: nn.Sequentialself.stage3: nn.Sequentialself.stage4: nn.Sequentialstage_names = ["stage{}".format(i) for i in [2, 3, 4]]for name, repeats, output_channels in zip(stage_names, stages_repeats,self._stage_out_channels[1:]):# 每个Stage的首个基础单元都需要进行下采样,其他单元不需要seq = [ShuffleUnit(input_channels, output_channels, 2)]for i in range(repeats - 1):seq.append(ShuffleUnit(output_channels, output_channels, 1))setattr(self, name, nn.Sequential(*seq))input_channels = output_channelsoutput_channels = self._stage_out_channels[-1]self.conv5 = nn.Sequential(nn.Conv2d(input_channels, output_channels, kernel_size=1, stride=1, padding=0, bias=False),nn.BatchNorm2d(output_channels),nn.ReLU(inplace=True))# 全局平局池化self.global_pool = nn.AdaptiveAvgPool2d((1, 1))# 全连接层self.fc = nn.Linear(output_channels, num_classes)# 权重初始化self.init_params()def init_params(self):for m in self.modules():if isinstance(m, nn.Conv2d):nn.init.kaiming_normal_(m.weight, mode='fan_out')if m.bias is not None:nn.init.zeros_(m.bias)elif isinstance(m, nn.BatchNorm2d):nn.init.ones_(m.weight)nn.init.zeros_(m.bias)elif isinstance(m, nn.Linear):nn.init.normal_(m.weight, 0, 0.01)nn.init.zeros_(m.bias)def forward(self, x):x = self.conv1(x)x = self.maxpool(x)x = self.stage2(x)x = self.stage3(x)x = self.stage4(x)x = self.conv5(x)x = self.global_pool(x)x = x.view(x.size(0), -1)x = self.fc(x)return xdef shufflenet_v2_x0_5(num_classes=1000):"""weight: https://download.pytorch.org/models/shufflenetv2_x0.5-f707e7126e.pth"""model = ShuffleNetV2(stages_repeats=[4, 8, 4],stages_out_channels=[24, 48, 96, 192, 1024],num_classes=num_classes)return model
def shufflenet_v2_x1_0(num_classes=1000):"""weight: https://download.pytorch.org/models/shufflenetv2_x1-5666bf0f80.pth"""model = ShuffleNetV2(stages_repeats=[4, 8, 4],stages_out_channels=[24, 116, 232, 464, 1024],num_classes=num_classes)return modeldef shufflenet_v2_x1_5(num_classes=1000):"""weight: https://download.pytorch.org/models/shufflenetv2_x1_5-3c479a10.pth"""model = ShuffleNetV2(stages_repeats=[4, 8, 4],stages_out_channels=[24, 176, 352, 704, 1024],num_classes=num_classes)return modeldef shufflenet_v2_x2_0(num_classes=1000):"""weight: https://download.pytorch.org/models/shufflenetv2_x2_0-8be3c8ee.pth"""model = ShuffleNetV2(stages_repeats=[4, 8, 4],stages_out_channels=[24, 244, 488, 976, 2048],num_classes=num_classes)return modelif __name__ == '__main__':device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")model = shufflenet_v2_x2_0().to(device)summary(model, input_size=(3, 224, 224))
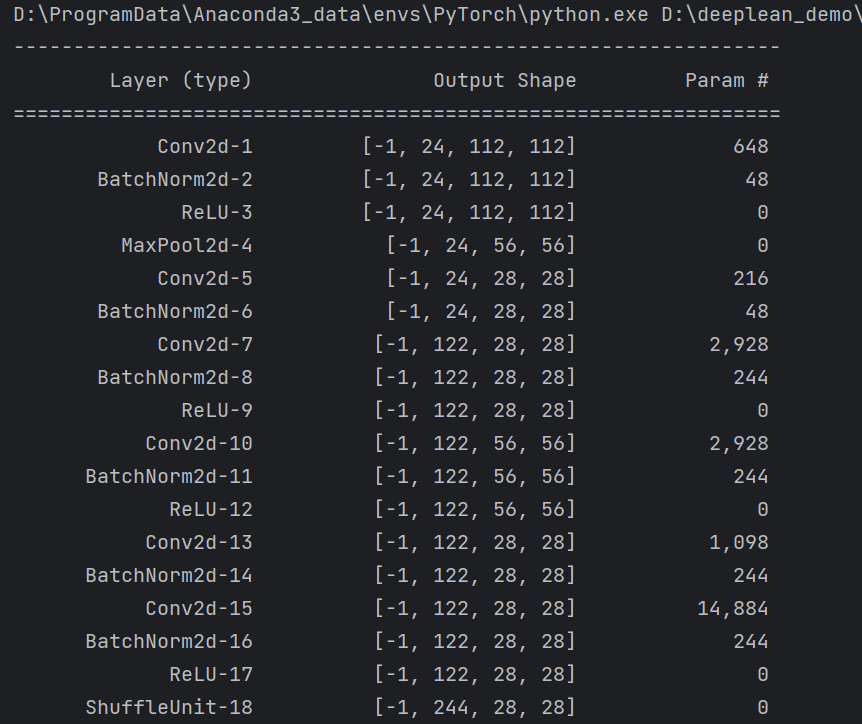
summary可以打印网络结构和参数,方便查看搭建好的网络结构。
总结
尽可能简单、详细的介绍了四条实用指导思想的原理,讲解了ShuffleNet_V2模型的结构和pytorch代码。