文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:枚举操作数
- 写在最后
Tag
【枚举】【数组】【2023-12-28】
题目来源
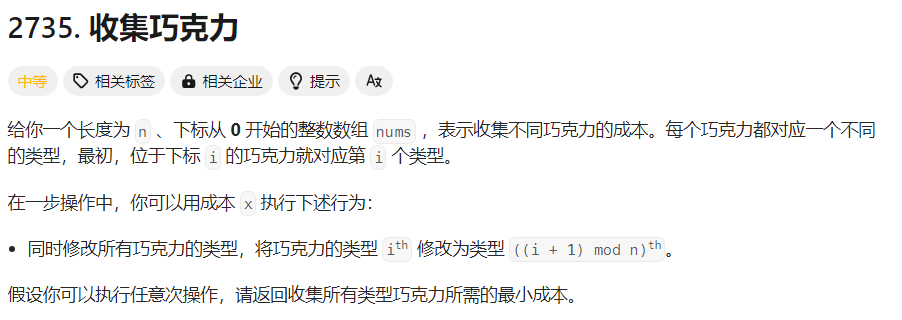
2735. 收集巧克力
题目解读
有长度为 n, 下标从 0 开始的整数数组 nums, 表示收集不同类型的巧克力的成本. nums[i] 表示收集类型 i 巧克力的成本.
在进行 k 次操作后(每次操作的成本为 x), 初始类型为 i 的巧克力需要 nums[(i + k) mod n] 的成本来收集. 我们也可以不进行任何操作,直接收集巧克力.
最后返回收集所有 n 种类型的巧克力的最小成本.
解题思路
方法一:枚举操作数
思路
对于初始类型为 i 的巧克力,如果我们一共进行了 k 次操作,那么相当于我们可以用:
n u m s [ i ] , n u m s [ ( i + 1 ) m o d n ] , . . . , n u m s [ ( i + k ) m o d n ] nums[i], nums[(i + 1) mod n], ..., nums[(i+k) mod n] nums[i],nums[(i+1)modn],...,nums[(i+k)modn]
中的任意成本去收集该类型的巧克力. 为了使成本最小, 我们一定要选择上述 k+1 个成本中的最小值进行收购. 当操作的次数为 n 时, 类型 i 的巧克力成本又会回到 nums[i], 因此操作次数不会超过 n-1.
于是,我们可以枚举所有的操作次数, 范围为 [0, n-1]. 当操作次数为 k 时,初始类型为 i 的巧克力成本可以这样表示:
{ f ( i , 0 ) = n u m s [ i ] f ( i , k ) = min { f ( i , k − 1 ) , n u m s [ ( i + k ) m o d n ] } \left\{ \begin{array}{l} f\left( i,\ 0 \right) =nums\left[ i \right]\\ f\left( i,\ k \right) =\min \left\{ f\left( i,\ k-1 \right) ,\ nums\left[ \left( i+k \right) \ mod\ n \right] \right\}\\ \end{array} \right. {f(i, 0)=nums[i]f(i, k)=min{f(i, k−1), nums[(i+k) mod n]}
此时, 操作次数为 k 时的最小成本为:
k ⋅ x + ∑ i = 0 n − 1 f ( i , k ) k\cdot x+\sum_{i=0}^{n-1}{f\left( i,k \right)} k⋅x+i=0∑n−1f(i,k)
最终答案即为所有 k ∈ [ 0 , n − 1 ] k∈[0,n−1] k∈[0,n−1] 时上式的最小值。
算法
class Solution {
public:long long minCost(vector<int>& nums, int x) {int n = nums.size();vector<int> f(nums);long long res = accumulate(f.begin(), f.end(), 0LL);for (int k = 1; k < n; ++k) {for (int i = 0; i < n; ++i) {f[i] = min(f[i], nums[(i+k) % n]);}res = min(res, static_cast<long long>(k) * x + accumulate(f.begin(), f.end(), 0LL));}return res;}
};
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2)。
空间复杂度: O ( n ) O(n) O(n)。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。