目录

收起

一 图像变换与平面坐标系的关系

二 平面坐标系与齐次坐标系

三 单应性变换

四 关于OpenCV中的相关API

五 深度学习在单应性方向的进展

单应性原理被广泛应用于图像配准，全景拼接，机器人定位SLAM，AR增强现实等领域。这篇文章从基础图像坐标知识系为起点，讲解图像变换与坐标系的关系，介绍单应性矩阵计算方法，并分析深度学习在单应性方向的进展。

本文为入门级文章，希望能够帮助读者快速了解相关内容。

单应性估计在图像拼接中的应用

一 图像变换与平面坐标系的关系

• 旋转：

将图形围绕原点 (0,0) 逆时针方向旋转 θ 角，用解析式表示为：

旋转

写成矩阵乘法形式：

• 平移：

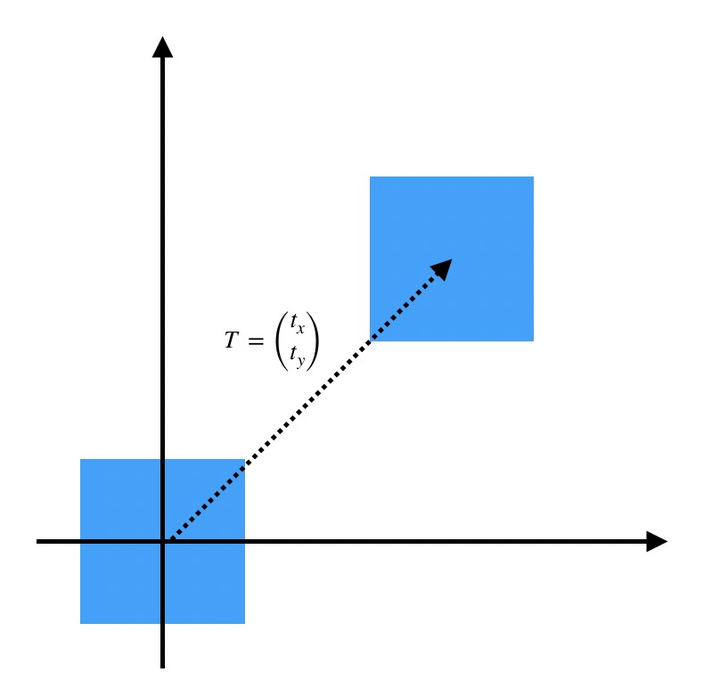
平移

但是现在遇到困难了，平移无法写成和上面旋转一样的矩阵乘法形式。所以引入齐次坐标 (x,y)⇔(x,y,1) ，再写成矩阵形式：

其中 I2×2=[1001] 表示单位矩阵，而 T2×1=[txty] 表示平移向量。

那么就可以把把旋转和平移统一写在一个矩阵乘法公式中，即刚体变换：

而旋转矩阵 R2×2 是正交矩阵（ RRT=RTR=I ）。

刚体变换：旋转+平移（正方形-正方形）

• 仿射变换

其中 A2×2=[a11a12a21a22] 可以是任意2x2矩阵（与 R 一定是正交矩阵不同）。

仿射变换（正方形-平行四边形）

可以看到，相比刚体变换（旋转和平移），仿射变换除了改变目标位置，还改变目标的形状，但是会保持物体的“平直性（如图形中平行的两条线变换后依然平行）”。

不同 A 和 T 矩阵对应的各种基本仿射变换：

• 透视变换（也称投影变换）

透视变换（正方形-任意四边形）

简单说，透视变换（也称投影变换）彻底改变目标的形状。

总结一下：

1. 刚体变换：平移+旋转，只改变物体位置，不改变物体形状。
2. 仿射变换：改变物体位置和形状，但是原来平行的边依然平行。
3. 透视变换（也称投影变换）：彻底改变物体位置和形状

我们来看看完整透视变换矩阵各个参数的物理含义：

其中 A2×2 代表仿射变换参数， T2×1 代表平移变换参数。

而 VT=[v1,v2] 表示一种“变换后边缘交点“关系，如：

至于 s 则是一个与 VT=[v1,v2] 相关的缩放因子。

一般情况下都会通过归一化使得 s=1 （原因见下文）。

二 平面坐标系与齐次坐标系

问题来了，齐次坐标到底是什么？

齐次坐标系 (x,y,w)∈P3 与常见的三维空间坐标系 (x,y,z)∈R3 不同，只有两个自由度：

而 w （其中 w>0 ）对应坐标 x 和 y 的缩放尺度。当 w=1 时：

特别的当 w=0 时，对应无穷远：

从二维平面上看， (x,y,w) 随 w 的变化在从原点到 (x,y) 的蓝虚线示意的射线上滑动：

三 单应性变换

• 单应性是什么？

此处给出单应性不严谨的定义：用 [无镜头畸变] 的相机从不同位置拍摄 [同一平面物体] 的图像之间存在单应性，可以用 [透视变换] 表示 。

注意：
单应性的严格定义与成立条件非常复杂，超出本文范围，有需要的朋友请自行查阅相关内容。

简单说就是：right view图像上的点可以经过透视变换到left view图像上对应位置。

其中 (xl,yl) 是Left view图片上的点， (xr,yr) 是Right view图片上对应的点。

• 那么这个 H3×3 单应性矩阵如何求解呢？

从更一般的情况分析，每一组匹配点 (xi,yi)→match(xi′,yi′) 有等式（15）成立：

由平面坐标与齐次坐标对应关系 (xw,yw)∈R2⇔(x,y,w)∈P3 ，上式可以表示为：

进一步变换为：

写成矩阵 AX=0 形式：

也就是说一组匹配点 (xi,yi)→match(xi′,yi′) 可以获得2组方程。

• 单应性矩阵8自由度

注意观察：单应性矩阵 H 与 aH 其实完全一样（其中 a≠0），例如：

即点 (xi,yi) 无论经过 H 还是 aH 映射，变化后都是 (xi′,yi′) 。

如果使 a=1h33 ，那么有:

所以单应性矩阵 H 虽然有9个未知数，但只有8个自由度。在求 H 时一般添加约束 h33=1，所以还有 h11∼h32 共8个未知数。

由于一组匹配点 (xi,yi)→match(xi′,yi′) 对应2组方程，那么只需要 n=4 组不共线的匹配点即可求解 H 的唯一解。

XIAOMI9拍摄，有镜头畸变

OpenCV已经提供了相关API，代码和变换结果如下。

import cv2
import numpy as npim1 = cv2.imread('left.jpg')
im2 = cv2.imread('right.jpg')src_points = np.array([[581, 297], [1053, 173], [1041, 895], [558, 827]])
dst_points = np.array([[571, 257], [963, 333], [965, 801], [557, 827]])H, _ = cv2.findHomography(src_points, dst_points)h, w = im2.shape[:2]im2_warp = cv2.warpPerspective(im2, H, (w, h))

可以看到：

1. 红框所在平面上内容基本对齐，但受到镜头畸变影响无法完全对齐；
2. 平面外背景物体不符合单应性原理，偏离很大，完全无法对齐。

• 传统方法估计单应性矩阵

一般传统方法估计单应性变换矩阵，需要经过以下4个步骤：

1. 提取每张图SIFT/SURF/FAST/ORB等特征点
2. 提取每个特征点对应的描述子
3. 通过匹配特征点描述子，找到两张图中匹配的特征点对（这里可能存在错误匹配）
4. 使用RANSAC算法剔除错误匹配
5. 求解方程组，计算Homography单应性变换矩阵

示例代码如下：

#coding:utf-8# This code only tested in OpenCV 3.4.2!
import cv2 
import numpy as np# 读取图片
im1 = cv2.imread('left.jpg')
im2 = cv2.imread('right.jpg')# 计算SURF特征点和对应的描述子，kp存储特征点坐标，des存储对应描述子
surf = cv2.xfeatures2d.SURF_create()
kp1, des1 = surf.detectAndCompute(im1, None)
kp2, des2 = surf.detectAndCompute(im2, None)# 匹配特征点描述子
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)# 提取匹配较好的特征点
good = []
for m,n in matches:if m.distance < 0.7*n.distance:good.append(m)# 通过特征点坐标计算单应性矩阵H
# （findHomography中使用了RANSAC算法剔除错误匹配）
src_pts = np.float32([kp1[m.queryIdx].pt for m in good]).reshape(-1,1,2)
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good]).reshape(-1,1,2)
H, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)
matchesMask = mask.ravel().tolist()# 使用单应性矩阵计算变换结果并绘图
h, w, d = im1.shape
pts = np.float32([[0,0], [0,h-1], [w-1,h-1], [w-1,0]]).reshape(-1,1,2)
dst = cv2.perspectiveTransform(pts, H)
img2 = cv2.polylines(im2, [np.int32(dst)], True, 255, 3, cv2.LINE_AA)draw_params = dict(matchColor = (0,255,0), # draw matches in green colorsinglePointColor = None,matchesMask = matchesMask, # draw only inliersflags = 2)im3 = cv2.drawMatches(im1, kp1, im2, kp2, good, None, **draw_params)

相关内容网上资料较多，这里不再重复造轮子。需要说明，一般情况计算出的匹配的特征点对 (xi,yi)→match(xi′,yi′) 数量都有 n≫4 ，此时需要解超定方程组（类似于求解线性回归时数据点的数量远多余未知数）。

另外有人在评论区提到逆透视变换

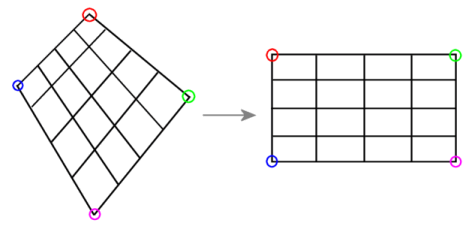
逆透视变换一般常用在自动驾驶场景中，把相机拍摄到的画面转换为俯视鸟瞰图，用于计算车辆前方可行驶区域等。实际上逆透视变换也是透视变换的一种特殊情况，只不过叫法不同而已，把不规则的图像变为规则俯视图（如下图，梯形变换为长方形）。

需要特别强调，根据单应性成立的基本条件，逆透视变换只在地平面内成立，两侧建筑、天空等不在地平面上的目标无法对应。

四 关于OpenCV中的相关API

首先需要说明，OpenCV中的图像行列 xcolyrow 坐标系与上文中的 xy 坐标系有一些差异。

在上述分析中使用的是 xy 坐标系；但是在OpenCV等常用图像库中往往使用以图像左上角为原点的 xcolyrow 坐标系，会导致OpenCV中的Homography矩阵与上述推导有一些差异（相当于y轴翻转了）。

在OpenCV中imgproc模块提供了warpPerspective()与warpAffine()两个函数

• warpPerspective 即透视变换函数

dst = cv2.warpPerspective(src, M, dsize, dst, flags, borderMode, borderValue)

其中 M 即为 3x3 变换矩阵。

• warpAffine 即为仿射变换函数

dst = cv2.warpAffine(src, M, dsize, dst, flags, borderMode, borderValue)

其中 M 即为 2x3 变换矩阵（由于仿射变换 3x3 矩阵最下面一行为 0 0 1，如公式7，所以也就简写为 2x3 了）

从原理上来说，仿射变换是透视变换的特例，所以可以用warpPerspective来计算仿射变换。但是实际中涉及到代码优化等问题，最好还是使用对应的API。

五 深度学习在单应性方向的进展

• HomographyNet（深度学习end2end估计单应性变换矩阵）

Deep Image Homography Estimation​arxiv.org/pdf/1606.03798.pdf

HomographyNet是发表在CVPR 2016的一种用深度学习计算单应性变换的网络，即输入两张图，直接输出单应性矩阵 H 。

在之前的分析中提到，只要有4组 (xi,yi)→match(xi′,yi′) 匹配点即可计算 H3×3 的唯一解。

相似的，只要有4组 (Δxi,Δyi) 也可以计算出 H3×3 的唯一解：

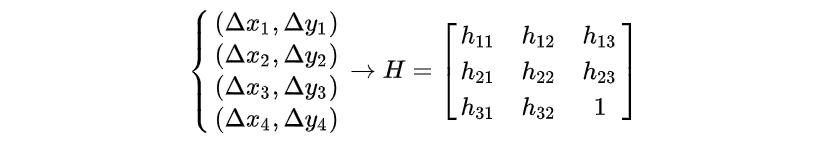
其中 Δxi=xi−xi′ 且 Δy=yi−yi′ 。

分析到这里，如果要计算 H ，网络输出可以有以下2种情况：

1. Regression：网络直接输出 (Δx1,Δy1)∼(Δx4,Δy4) 共8个数值

这样设置网络非常直观，使用L2损失训练，测试时直接输出8个float values，但是没有置信度confidence。即在使用网络时，无法知道当前输出单应性可靠程度。

2. Classification：网络输出 (Δx1,Δy1)∼(Δx4,Δy4) 共8个值的量化值+confidence

这时将网络输出每个 Δxi 和 Δyi 量化成21个区间，用分类的方法判断落在哪一个区间。训练时使用Softmax损失。相比回归直接输出数值，量化必然会产生误差，但是能够输出分类置信度评判当前效果好坏，更便于实际应用。

另外HomographyNet训练时数据生成方式也非常有特色。

1. 首先在随机 p 位置获取正方形图像块Patch A
2. 然后对正方形4个点进行随机扰动，同时获得4组 (Δxi,Δyi)
3. 再通过4组 (Δxi,Δyi) 计算 HAB
4. 最后将图像通过 HBA=(HAB)−1 变换，在变换后图像 p 位置获取正方形图像块Patch B

那么图像块A和图像块B作为输入，4组 (Δxi,Δyi) 作为监督Label，进行训练

可以看到，在无法提取足够特征点的弱纹理区域，HomographyNet相比传统方法确实有一定的优势：

• Spatial Transformer Networks（直接对CNN中的卷积特征进行变换）

Spatial Transformer Networks​arxiv.org/abs/1506.02025

其实早在2015年，就已经有对CNN中的特征进行变换的STN结构。

假设有特征层 U ，经过卷积变为 V ，可以在他们之间插入STN结构。这样就可以直接学习到从特征 U 上的点 (xiu,yiu) 映射到特征 V 对应点 (xiv,yiv) 的仿射变换。

其中 Aθ 对应STN中的仿射变换参数。STN直接在特征维度进行变换，且可以插入轻松任意两层卷积中。但是实际使用中STN效果并没有想象的那么好，所以也没引起什么轰动。

• DELF: DEep Local Features（深度学习提取特征点与描述子）

之前提到传统方法使用SIFT和Surf等特征点估计单应性。显然单应性最终估计准确度严重依赖于特征点和描述子性能。Google在ICCV 2017提出使用使用深度学习提取特征点。

tensorflow/models/delf​github.com/tensorflow/models/tree/master/research/delf​编辑

考虑到篇幅，这里不再展开DELF，请有兴趣的读者自行了解相关内容。

---

相机数学模型点这里：

相机模型与视觉测距不完全指南270 赞同 · 15 评论文章​编辑

对极几何点这里：

从对极几何恢复相机运动187 赞同 · 19 评论文章​编辑

创作不易，求点赞！感谢小可爱们的支持！