文章目录
- 1954. 收集足够苹果的最小花园周长
- 思考:
- 暴力枚举
- 代码实现
- 二分查找
- 代码实现
1954. 收集足够苹果的最小花园周长
1954. 收集足够苹果的最小花园周长
难度: 中等
题目大意:
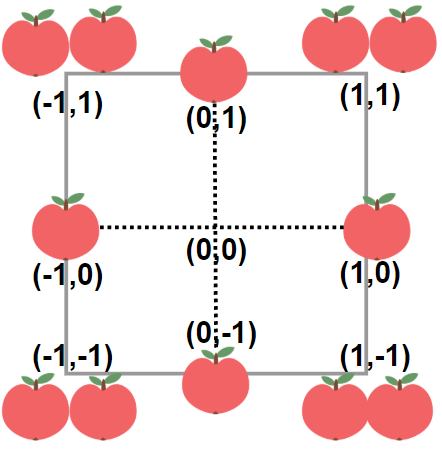
给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。
你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。
给你一个整数 neededApples ,请你返回土地的 最小周长 ,使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。
1 <= neededApples <= 10^15
思考:
这个图形是很对称的,那么很自然会想到要推导一个用边长来表示边上的所有苹果数量,而且我们只需要计算出第一象限的苹果即可,假设最右边的的横坐标是x,那我们只需要计算(x, 0) 到 (x, x),然后根据对称性乘以4,然后对边长上的苹果求一个和
公式推导:
∑ x 2 x r = 3 x ( x + 1 ) 2 , 边上苹果数 = 4 ∗ ∑ x 2 x r = 6 x ( x + 1 ) = 6 ( x 2 + x ) \sum_x^{2x}{r} = \frac {3x(x + 1)}{2},边上苹果数 = 4 * \sum_x^{2x}{r} =6x(x + 1)=6(x^2 + x) x∑2xr=23x(x+1),边上苹果数=4∗x∑2xr=6x(x+1)=6(x2+x)
∑ 0 n r 2 = n ( n + 1 ) ( 2 n + 1 ) 6 \sum_0^nr^2 = \frac{n(n + 1)(2n + 1)}6 0∑nr2=6n(n+1)(2n+1)
∑ 苹果 = ∑ 0 n 6 ( x 2 + x ) = 2 n ( n + 1 ) ( 2 n + 1 ) \sum苹果 = \sum_0^n6(x^2 + x) = 2n(n + 1)(2n + 1) ∑苹果=0∑n6(x2+x)=2n(n+1)(2n+1)
就有了下面两种思路:
暴力枚举
我们至于要枚举边长,如果达到了要求,直接返回即可
代码实现
class Solution {
public:using LL = long long;long long minimumPerimeter(long long neededApples) {LL res = 0, sum = 0;for (int i = 0; ; i ++) {sum += 12 * (LL)i * i;if (sum >= neededApples) {res = i;break;}}return res * 8;}
};
考虑优化方案, 要满足2n(n + 1)(2n + 1) - k >= 0 我们画出这个图像

我们只需要求出与x正方向的交点即可,就有了下面这个思路
二分查找
注意到,在x0左侧的这一部分都是小于0的,在x0的右侧都是大于0的,这样就可以二分了
代码实现
class Solution {
public:using LL = long long;long long minimumPerimeter(long long neededApples) {;double l = 0, r = 70000;auto check = [&](double mid) -> bool {return 2 * mid * (mid + 1) * (2 * mid + 1) - neededApples < 0;};while (r - l > 1e-6) {double mid = (l + r) / 2;if (check(mid)) l = mid;else r = mid;}return ceil(l) * 8;}
};
ceil(x)函数是对x上取整
【微语】做你自己,因为其他角色都已经有人扮演了。
结束了