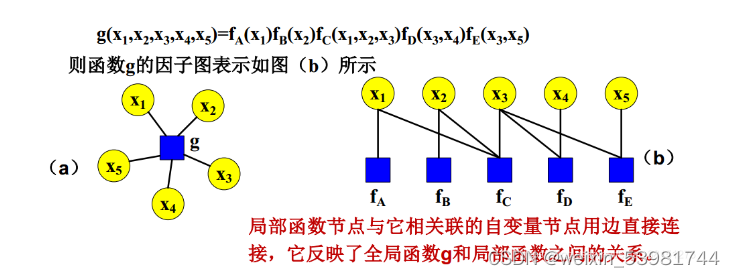
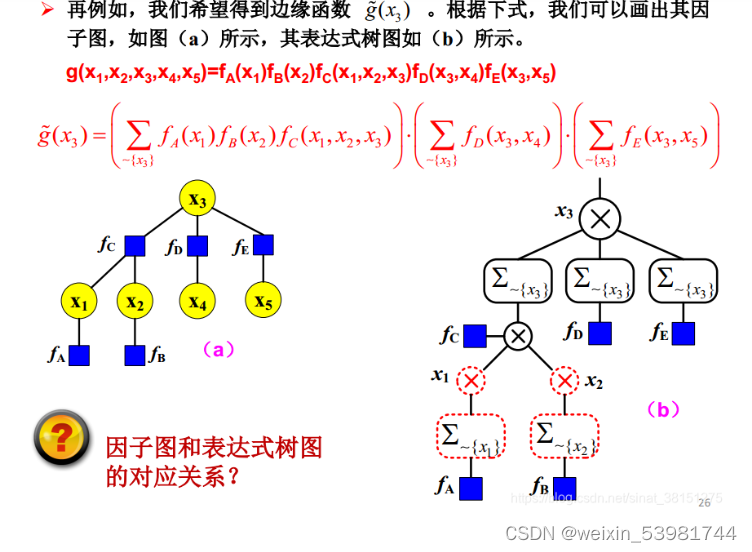
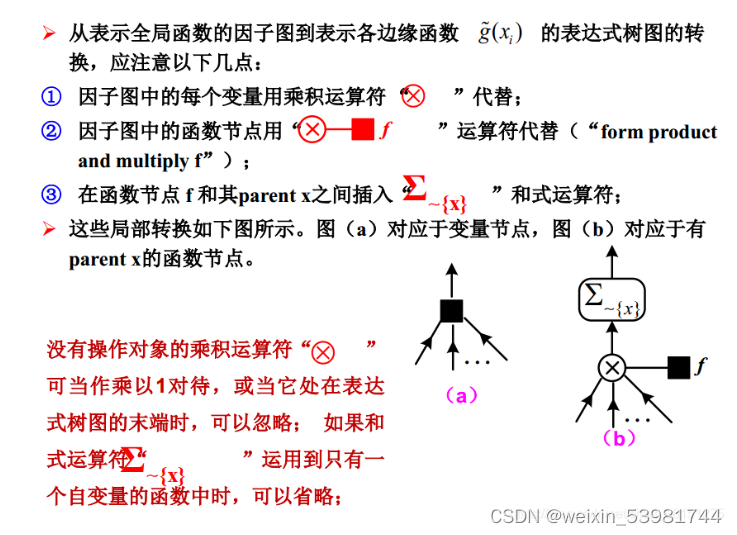
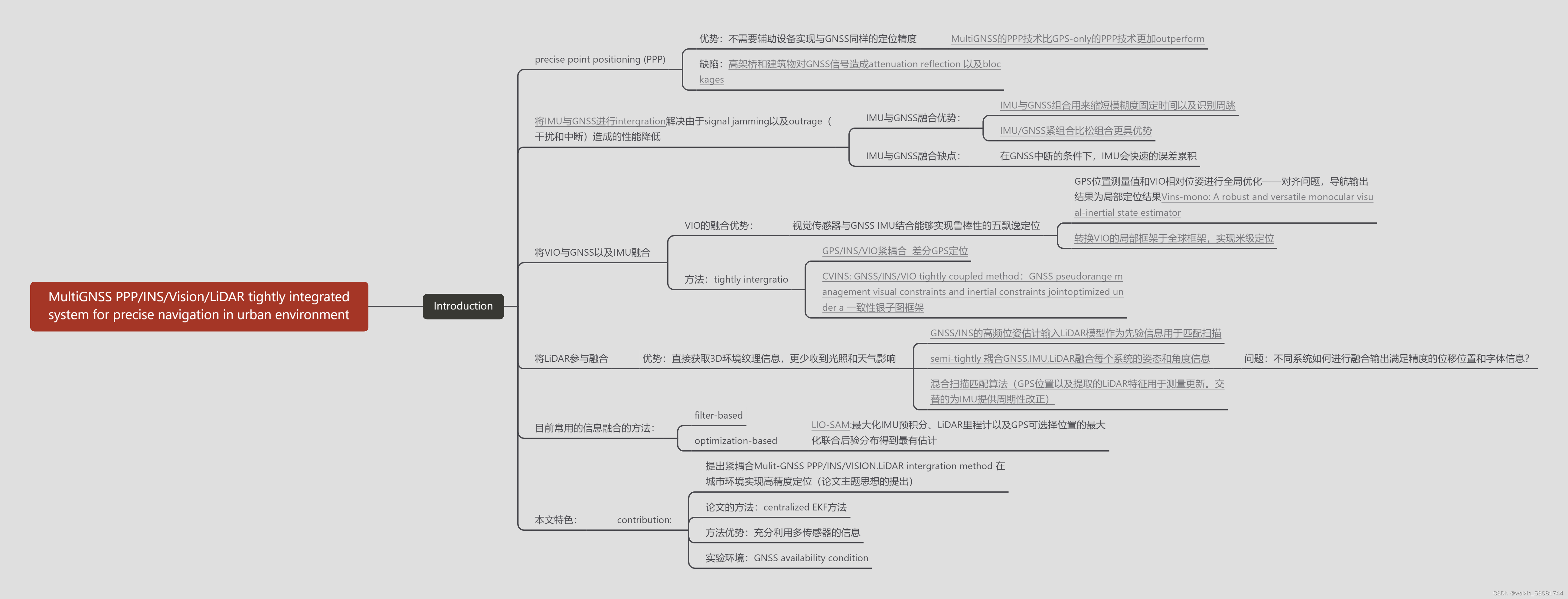
【多传感器融合导航论文阅读】
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/309258.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
css 用多个阴影做出光斑投影的效果 box-shadow
css 用多个阴影做出光斑投影的效果 box-shadow
你首先需要知道的一点是 box-shadow 可以接收多个值,也就是可以设置多个阴影,这样就可以做一个类似光斑投影的效果。
一、效果 二、代码
里面用到了我一些 scss 工具方法,不过不影响…
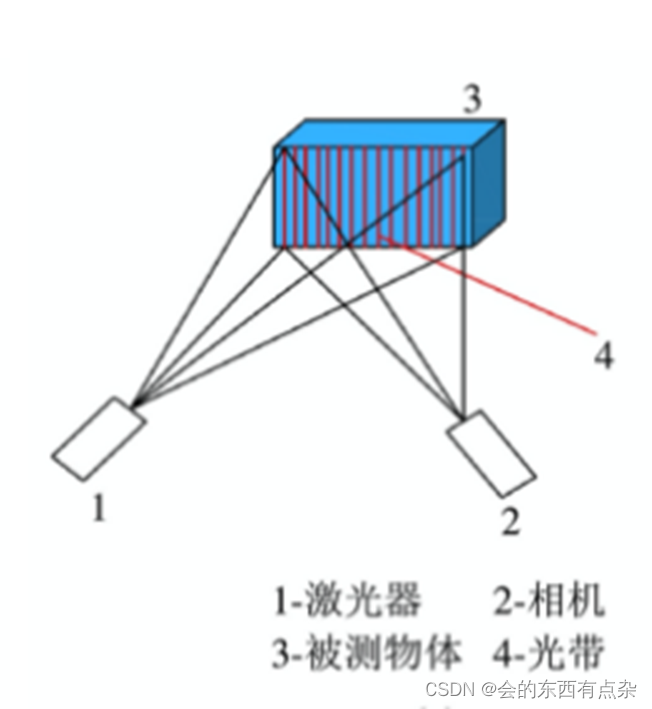
3D视觉-结构光测量-多线结构光测量
工作原理 多线结构光测量在测量方式上类似上述线结构光测量,但是两者也有着一些明显的差别。这种形式的结构光测量,也常常被成为面结构光测量。首先激光器发出电光源通过通过光栅的调制产生多个切片光束,这些切片光束照射到待测物体表面后形成…
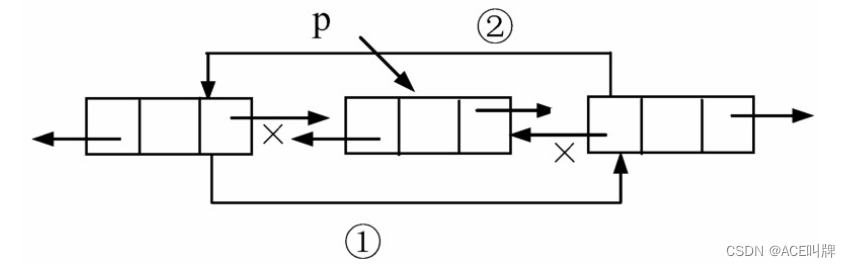
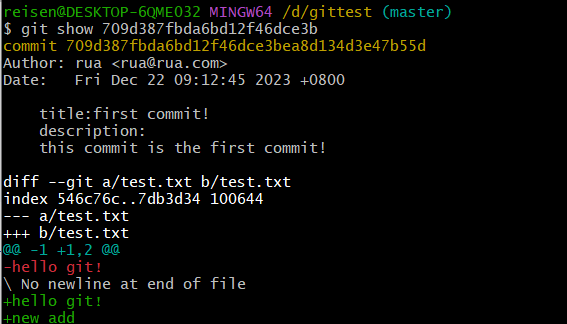
Git基础学习_p1
文章目录 一、前言二、Git手册学习2.1 Git介绍&前置知识2.2 Git教程2.2.1 导入新项目2.2.2 做更改2.2.3 Git追踪内容而非文件2.2.4 查看项目历史2.2.5 管理分支🔺2.2.6 用Git来协同工作2.2.7 查看历史 三、结尾 一、前言
Git相信大部分从事软件工作的人都听说过…
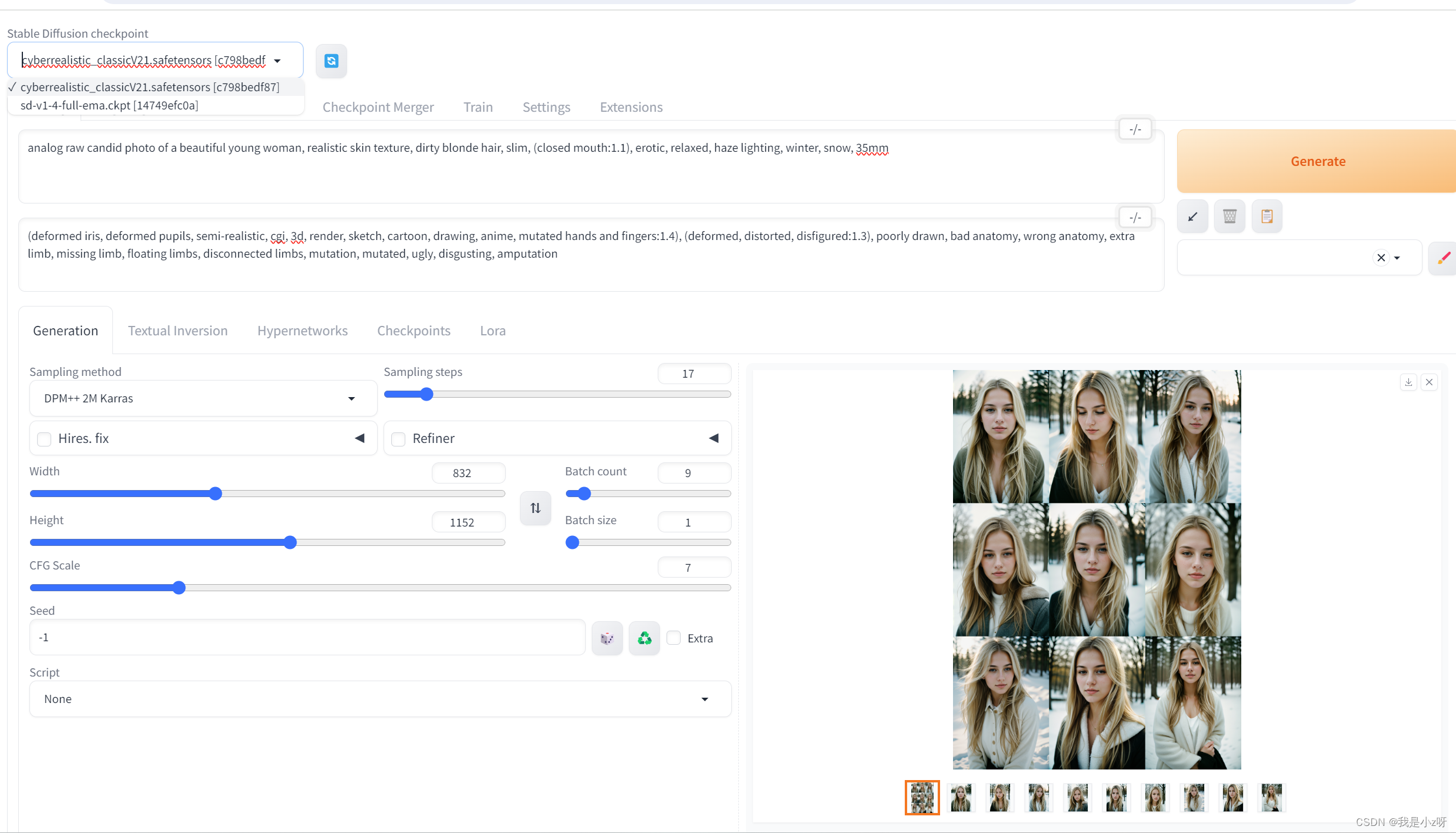
win部署stable-diffusion
win部署stable-diffusion 1.环境2.模型3.使用4.效果 1.环境
首先下载stable-diffusion-webui,这个包了一层ui,特别好用。
git clone https://github.com/AUTOMATIC1111/stable-diffusion-webui.git然后搭建conda环境。 这里的pytorch,自己去…
鸿蒙HarmonyOS-带笔锋手写板(三)
笔者用ArkTS 写了一个简单的带笔锋的手写板应用,并且可以将手写内容保存为图片。
一、效果图 手写效果如下(在鸿蒙手机模拟器上运行,手写时反应可能会有点慢) 二、实现方法
参考文章:
支持笔锋效果的手写签字控件_a…
在Linux上搭建Maven仓库的实战教程
引言
在Java开发中,Maven作为项目构建和依赖管理的重要工具,其仓库的搭建至关重要。本文将手把手教你如何在Linux系统上安装并配置Nexus Repository Manager 3(简称Nexus 3),从而创建一个私有的Maven仓库。
步骤一&a…
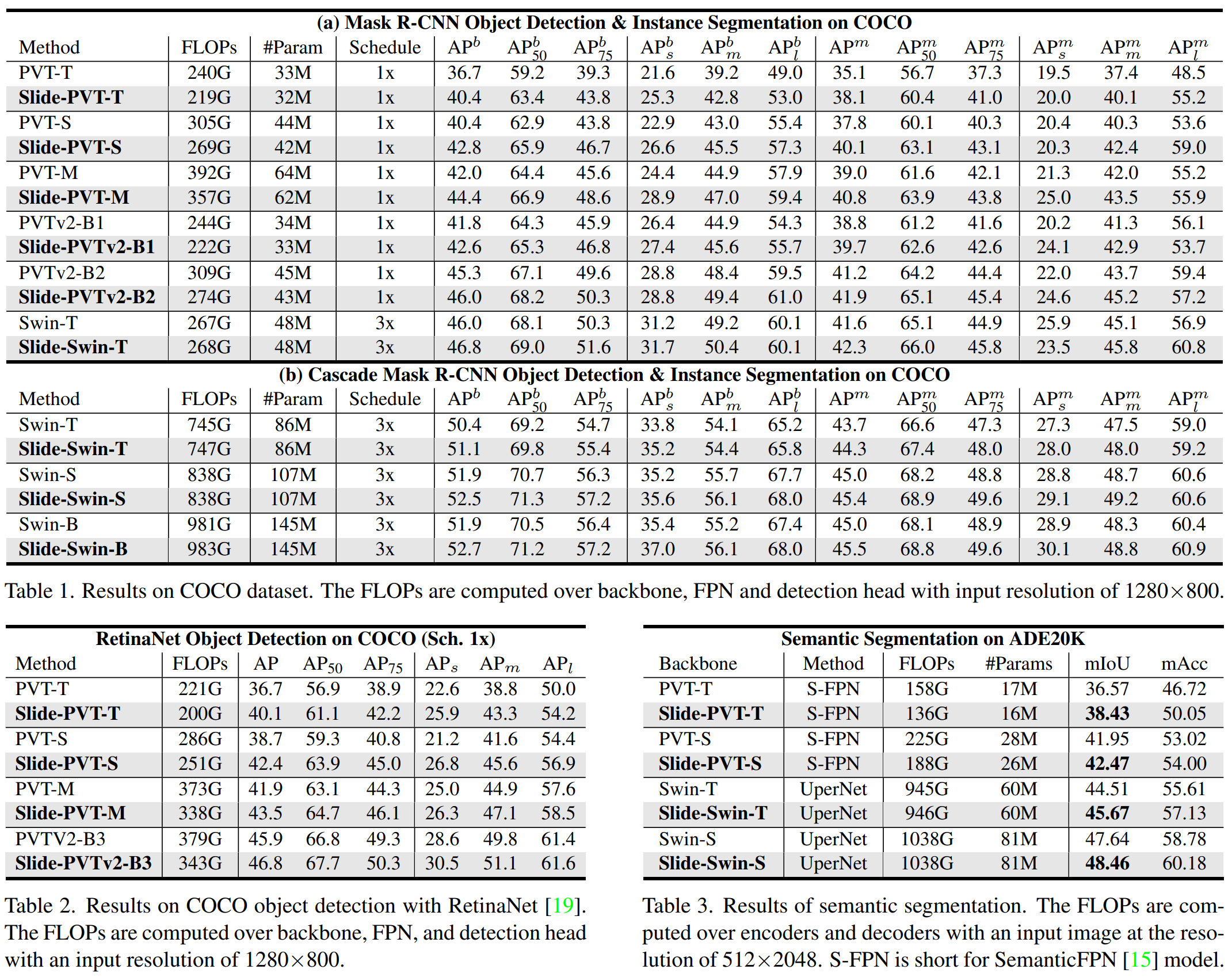
论文阅读——Slide-Transformer(cvpr2023)
Slide-Transformer: Hierarchical Vision Transformer with Local Self-Attention 一、分析
1、改进transformer的几个思路:
(1)将全局感受野控制在较小区域,如:PVT,DAT,使用稀疏全局注意力来…
JS 嵌套循环之退出顶层循环
我们常常写循环的时候,可能会遇到嵌套循环,如果出现退出循环,一层还好,多层循环就费劲了,传统做法是加 flag,如下:
for (let i 0; i < 10; i) {let flag falsefor (let j 0; j < 5; j…
oCPC实践录 | oCPM的秘密
前言
笔者从这几方面介绍oCPM,并一一分析平台侧宣称的oCPM相比oCPC的优势,并解开其中的秘密。 1)什么是oCPM? 2)oCPC与oCPM的异同 3)平台宣称oCPM的优势 4)oCPM真正的秘密 5)oCPM下的点击率与…