【动态规划精选题目】3、简单多状态模型-编程知识

此动态规划系列主要讲解大约10个系列【后续持续更新】

本篇讲解简单多状态模型中的9道经典题，会在讲解题目同时给出AC代码

1、按摩师

2、力扣198:打家劫舍1

3、打家劫舍II

4、删除并获得点数

5、粉刷房子

6、力扣309:买卖股票的最佳时机含冷冻期

7、买卖股票的最佳时机含手续费

8、买卖股票的最佳时机III

9、买卖股票的最佳时机IV

1、按摩师

示例分析：

class Solution {
public:int massage(vector<int>& nums) {int n = nums.size();if (n == 0) return 0;//创建两个dp表f和gvector<int> f(n);//n个数据都会初始化为0auto g = f;//创建g表f[0] = nums[0]; //初始化for (int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[n - 1], g[n - 1]); }
};

借多状态dp的题说明一下，怎么判断是一维dp还是二维dp呢？

是由状态表示决定的，如果一维数组能表示清楚，就用一维的，表示不清楚，就可以尝试增加维数，用二维的，有时候其实三维的也有，但是情况少。

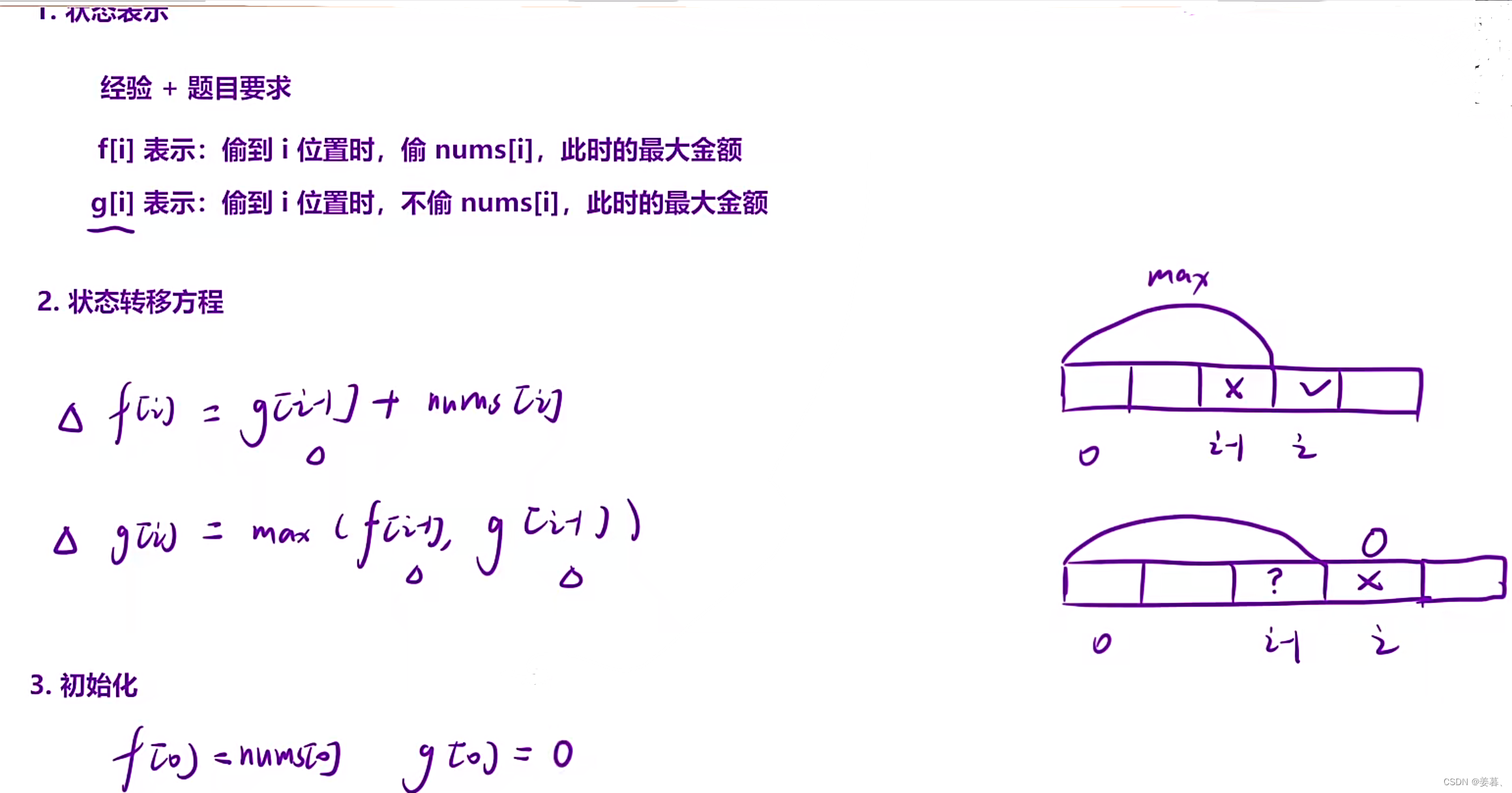
2、力扣198:打家劫舍1

这道题跟上道题的按摩师的思路和代码基本一样

class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();vector<int> f(n);auto g = f;f[0] = nums[0];for (int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(g[i - 1], f[i - 1]);}return max(f[n - 1], g[n - 1]);}
};

3、打家劫舍II

这道题只是在上一道题的打家劫舍1中加了一个限制条件，即首尾也算相连，不能都偷窃，所以只需分类讨论下这个情况，再转换为打家劫舍1即可（下面的rob1表示的是可以偷的范围，也就是可以用打家劫舍1来求解的地方）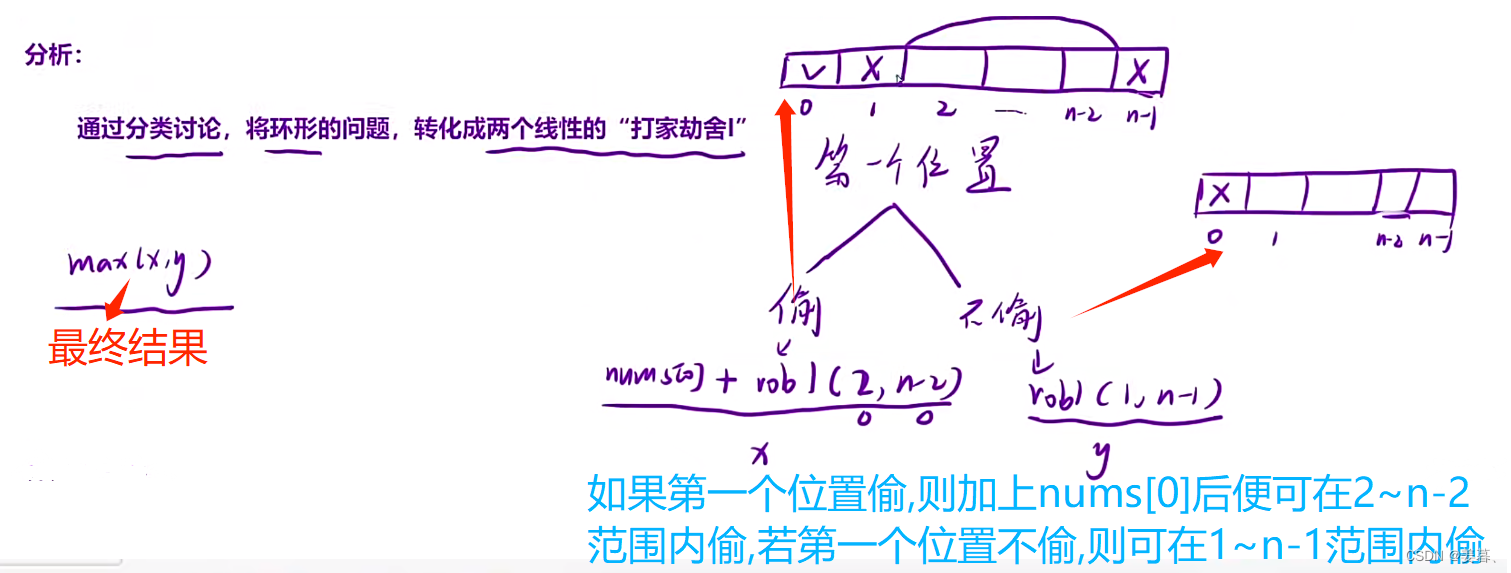

class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();return max(nums[0] + rob1(nums, 2, n - 2), rob1(nums, 1, n - 1));}int rob1(vector<int>& nums, int left, int right){if (left > right) return 0;//处理边界条件int n = nums.size();//按理说开right-left+1个空间即可，但这里多开几个也没事vector<int> f(n);auto g = f;f[left] = nums[left];//初始化for (int i = left + 1; i <= right; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[right], g[right]);}
};

4、删除并获得点数

动态规划的预处理思路：

其实上面的思想就是利用哈希表中的直接映射法，那么这种方法就要找nums数组中的最大值，但是题目中已经给出了nums数组中每个值的范围，故可以直接开空间大小为最大值。并且这种方法既做到了数据有序又做到了连续

整体思路：

class Solution {
public:int deleteAndEarn(vector<int>& nums) {const int N = 10001;//数组中的最大值为1万，多开1个防止越界问题//1、预处理int arr[N] = {0};for (const auto& x : nums) arr[x] += x;//2、利用打家劫舍思路求解该问题vector<int> f(N);auto g = f;//这里不用初始化了，因为f[0]=arr[0],可arr[0]本来就=0for (int i = 1; i < N; i++){f[i] = g[i - 1] + arr[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[N - 1], g[N - 1]);}
};

5、粉刷房子

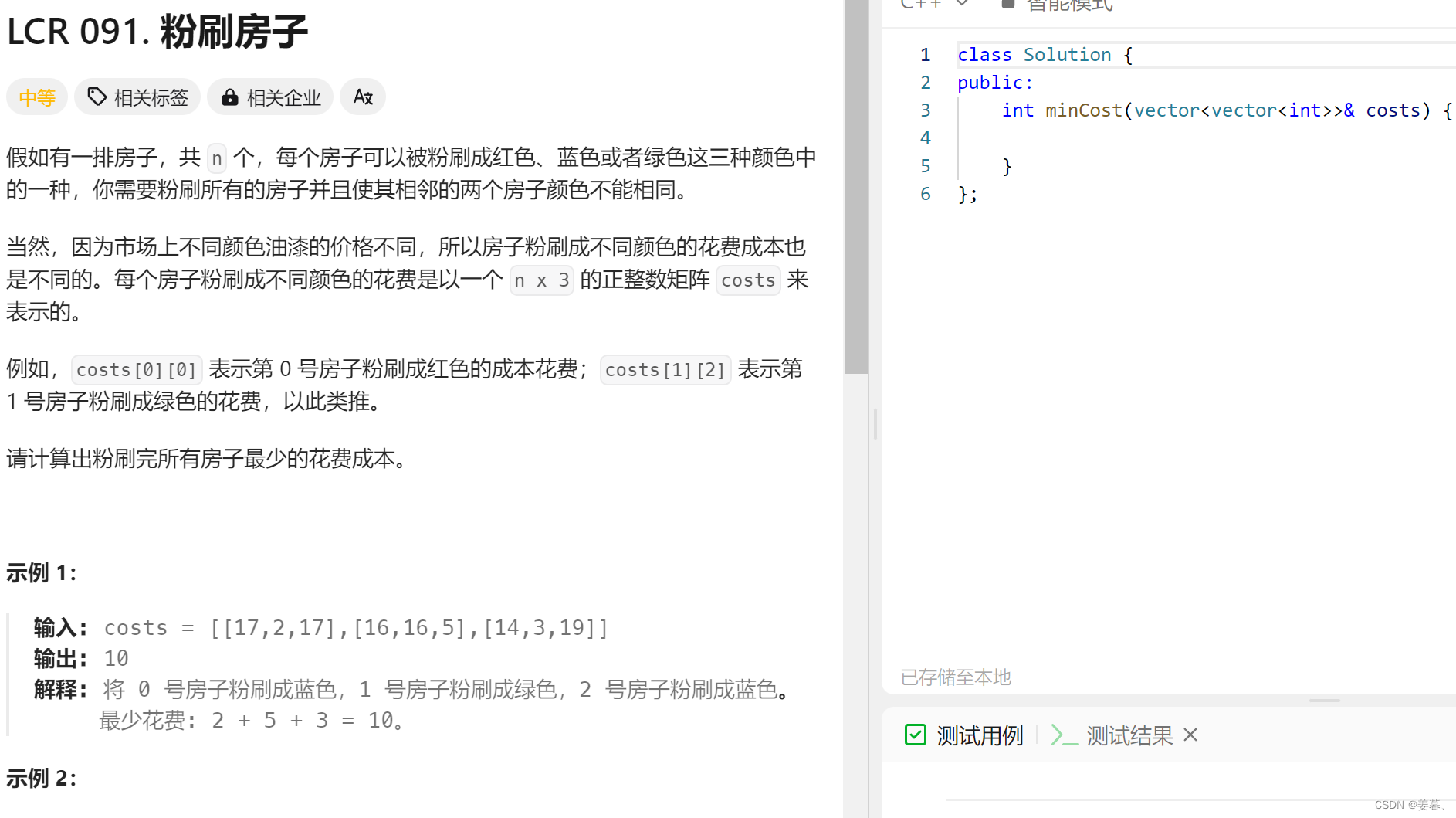
解释示例1和示例2：

也就是判断当前位置是第几个房子，只需看行即可，列是代表颜色的

总体思路：

下面说的位置可以理解为是一个房子

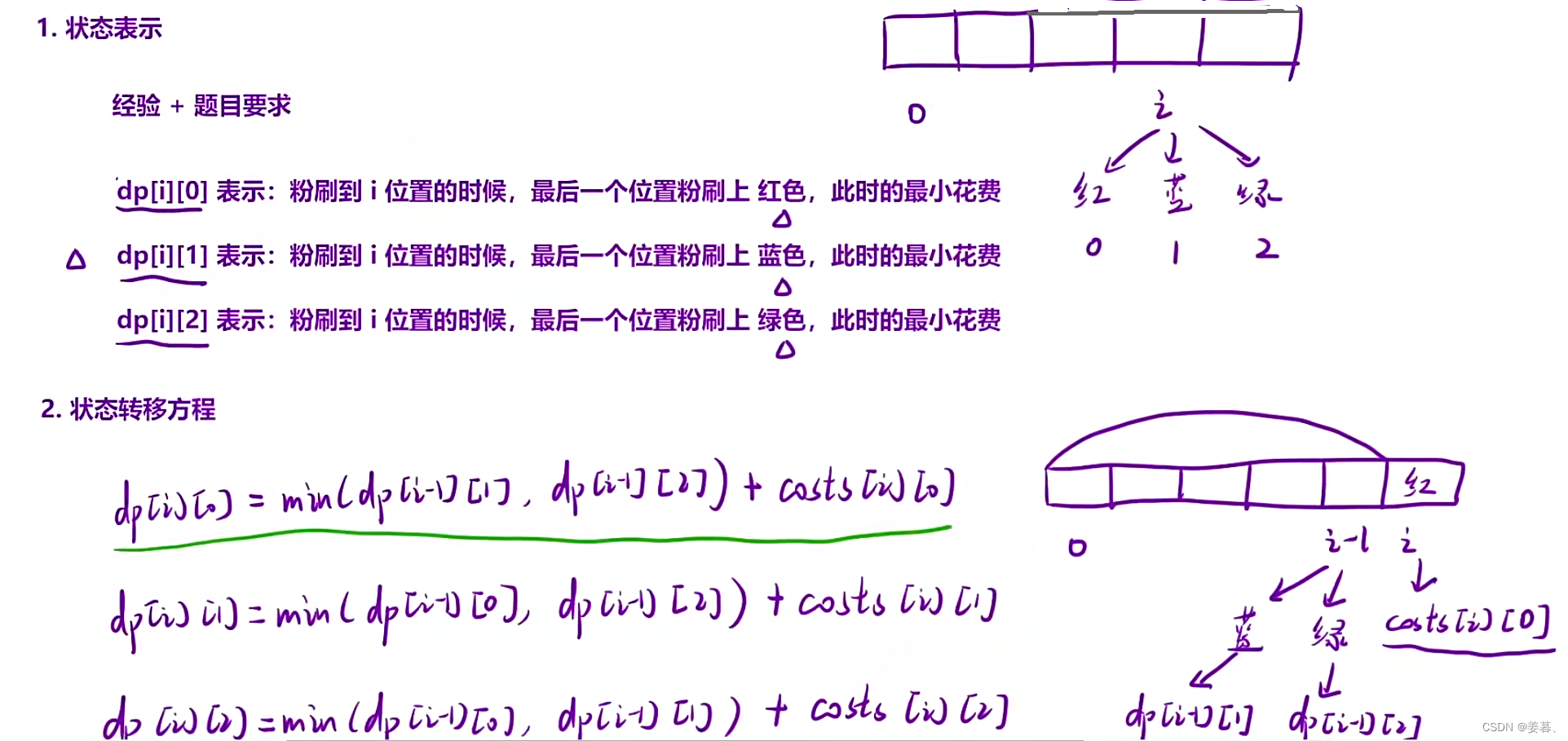
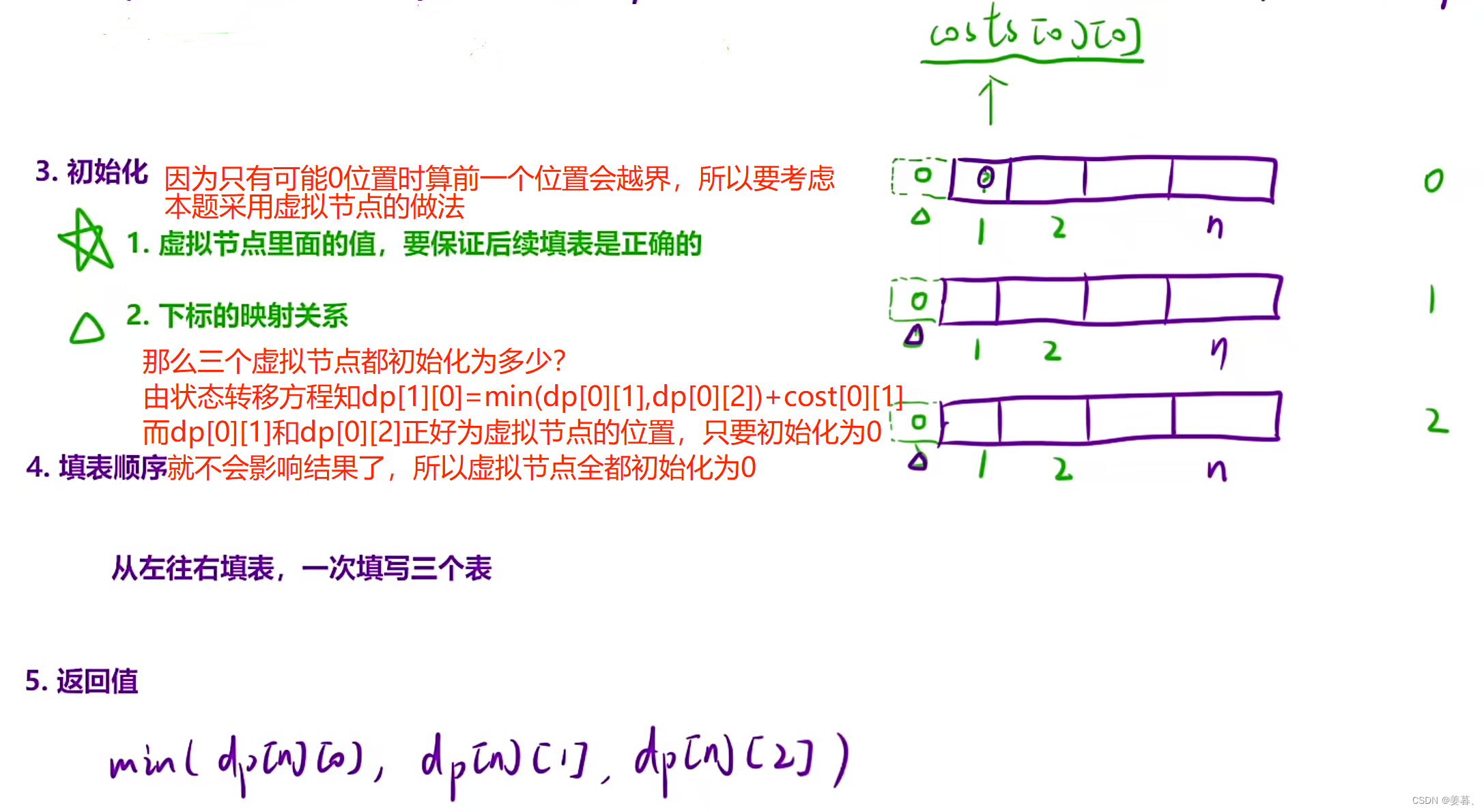
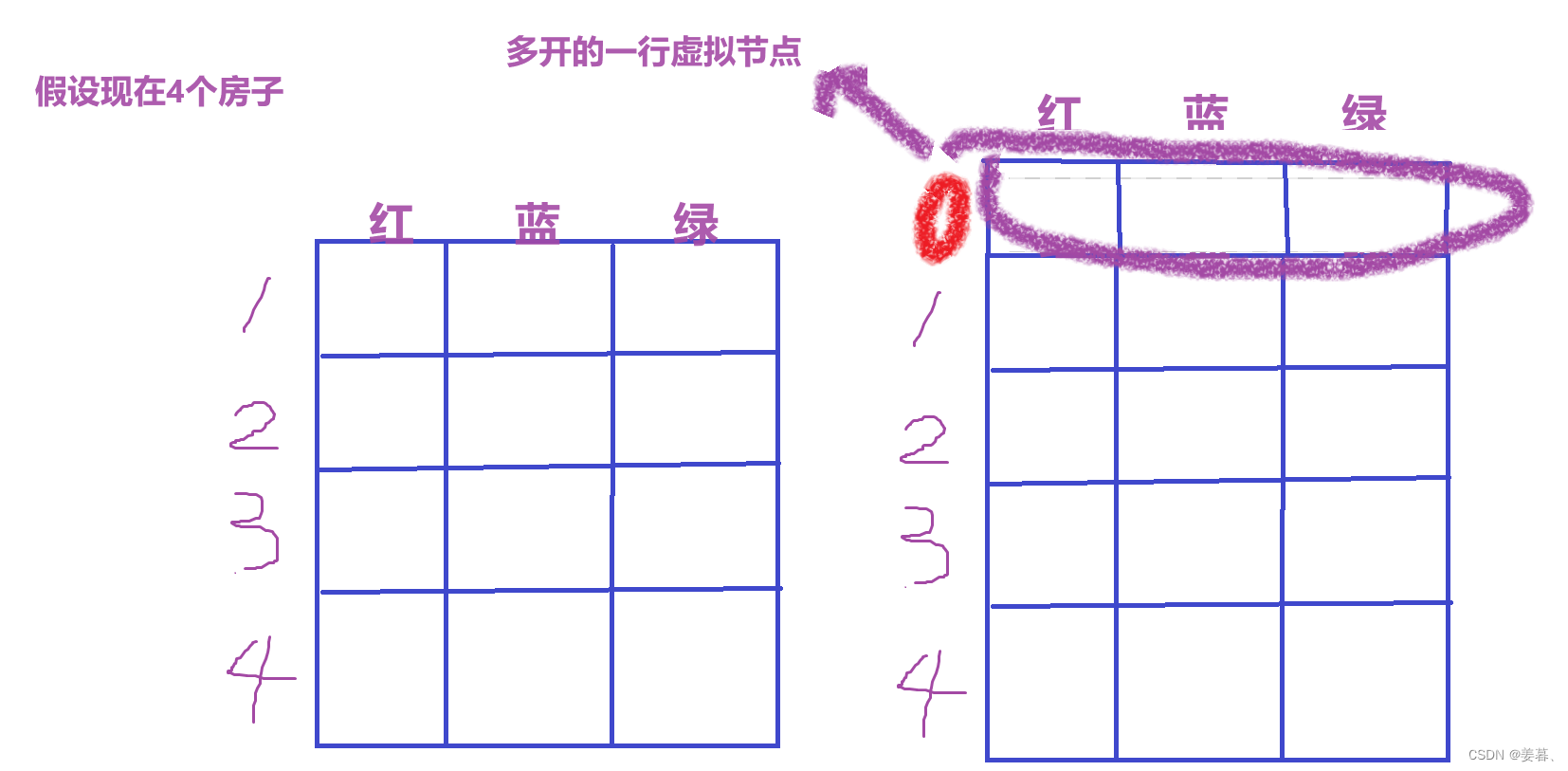
理解本题的虚拟节点：

class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();//得到的是行数，即现有的房子数vector<vector<int>> dp(n + 1, vector<int> (3));//多开一行给虚拟节点//从上到下遍历每个房子，算出每个房子对应不同颜色的价格for (int i = 1; i <= n; i++){//因为多开了一个虚拟节点，所以要加上cost[i-1][0]，这里要用i-1才行dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i- 1][0];dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i- 1][1];dp[i][2] = min(dp[i - 1][1], dp[i - 1][0]) + costs[i- 1][2];}return min(min(dp[n][0], dp[n][1]), dp[n][2]);}
};

6、力扣309:买卖股票的最佳时机含冷冻期

题目分析：

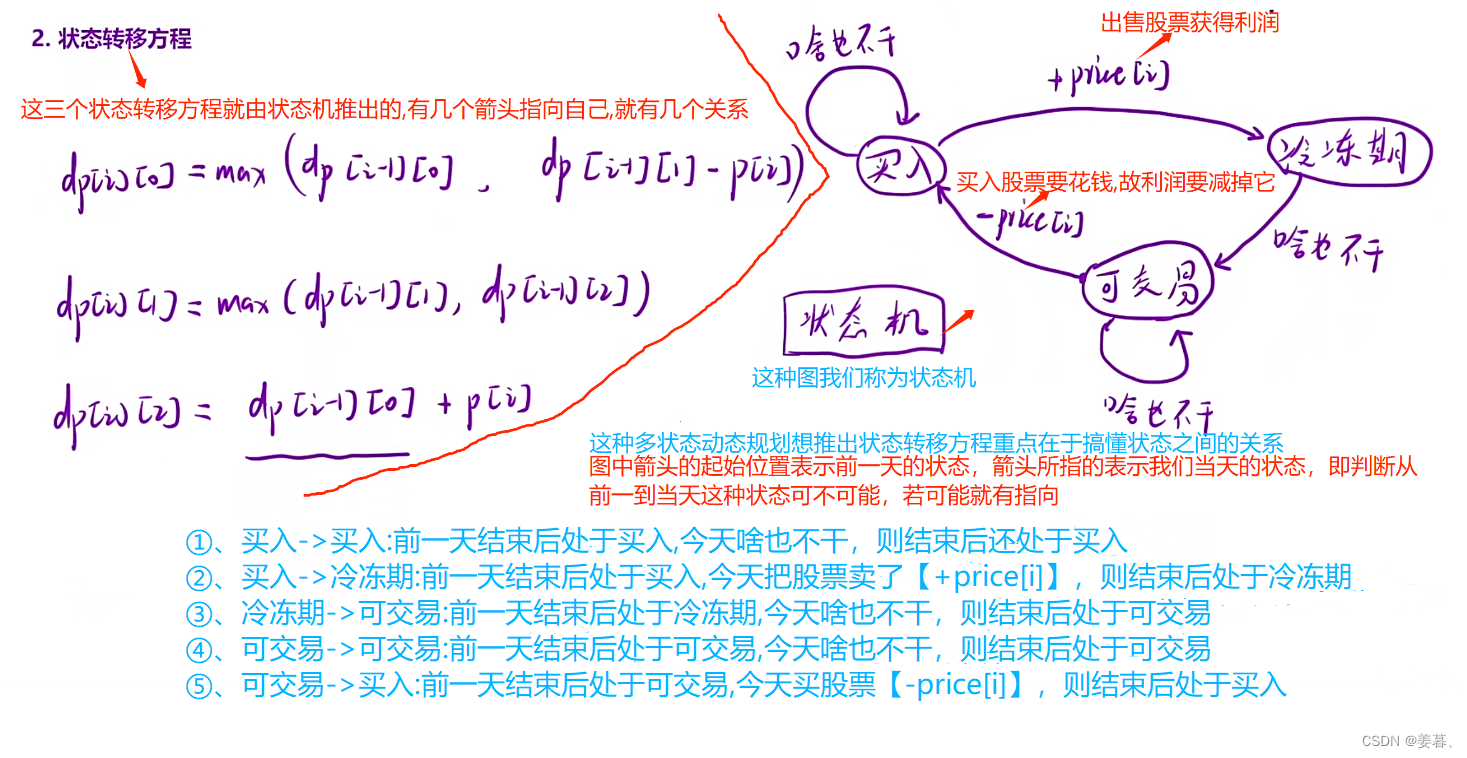
如果是多状态，并且多状态之间可以相互转移的话，为了不忽略某种状态，我们可以画一个图，如下图，我们也称为这种图为状态机

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(3));//三个dp表dp[0][0] = -prices[0];//初始化 for (int i = 1; i < n; ++i){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}//最佳答案一定不会是dp[n - 1][0]，所以最后不用考虑在内return max(dp[n - 1][1], dp[n - 1][2]);}
};

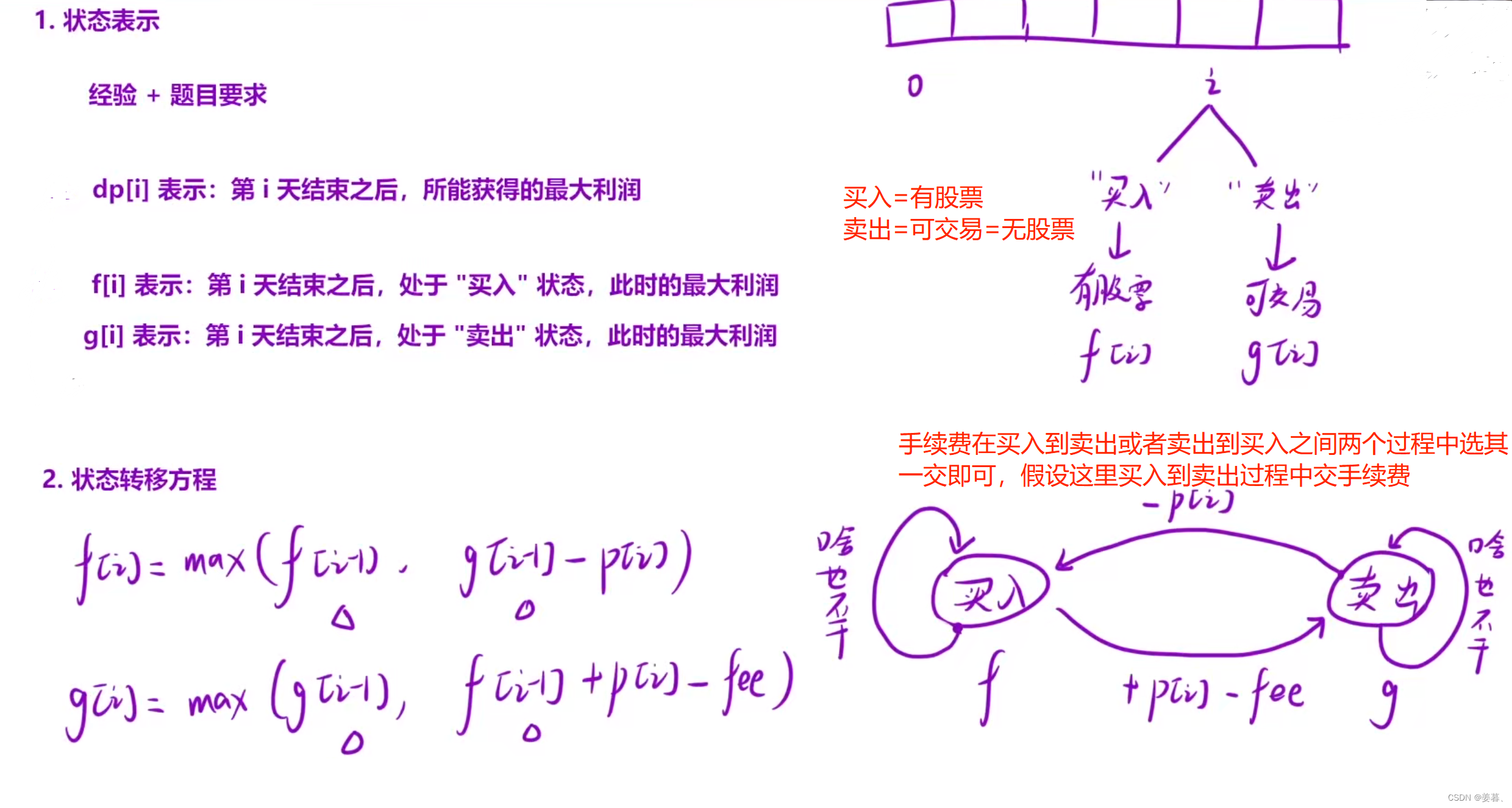
7、买卖股票的最佳时机含手续费

示例解释：

箭头起始位置：前一天结束后的状态，箭头指向位置：当天结束状态

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<int> f(n);auto g = f;f[0] = -prices[0];//初始化：第0天结束后处于买入状态for (int i = 1; i < n; i++){f[i] = max(f[i- 1], g[i - 1] - prices[i]);g[i] = max(f[i - 1] + prices[i] - fee, g[i - 1]);}//最后一天手里还有股票，肯定就不是最优解，故不用考虑return g[n - 1];}
};

当然,像之间那种开二维数组也可以，但是三种状态及以上才推荐开二维数组，下面这么写也可以

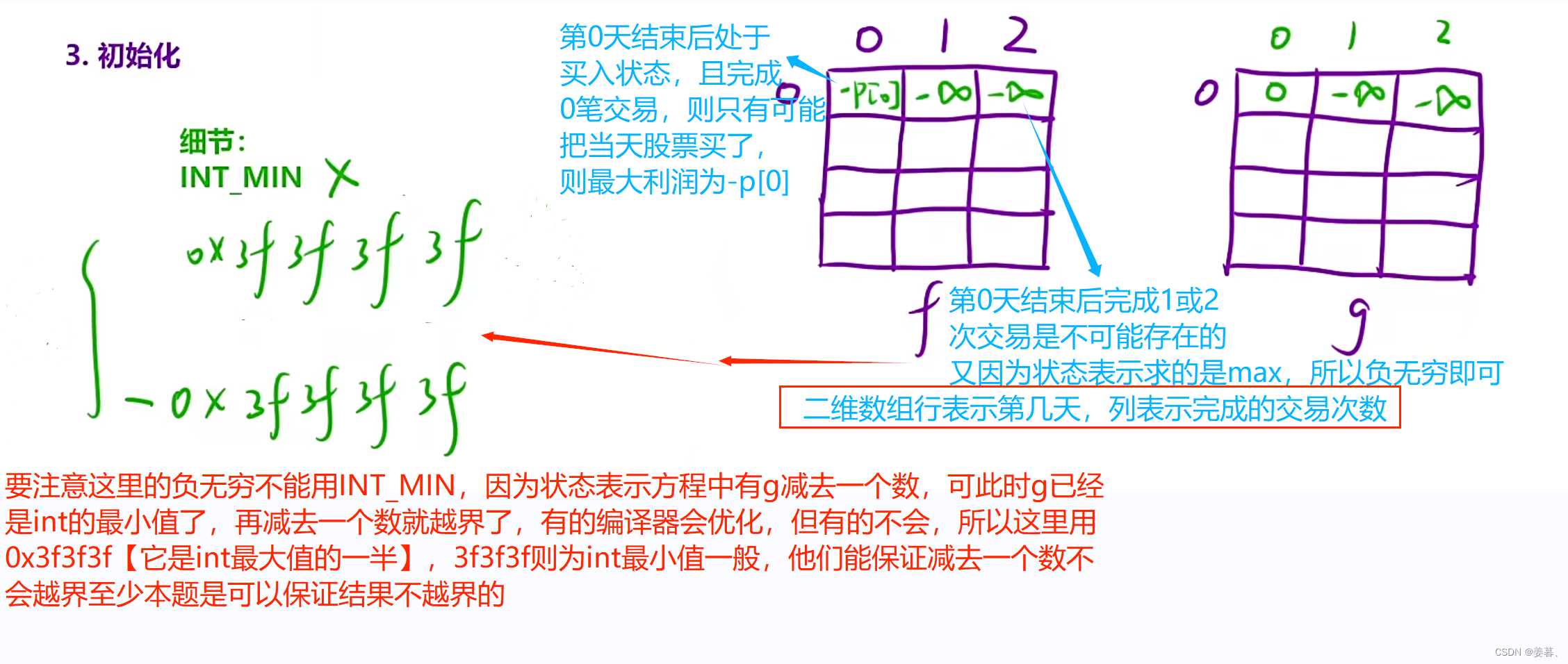
8、买卖股票的最佳时机III

示例分析：

此题复杂在还要考虑交易的次数。

买入是指手里有股票的状态，卖出是指手里没股票，是一个可交易的状态。下图的线的含义，线的起点表示前一天结束后的状态，线表示当天的操作，箭头所指的表示当天结束后的状态

但是因为f和g表初始化的不一致，可又不想在循环外再初始化哪个特例，就用稍微修改状态转移方程的方法来便于统一的初始化

class Solution {
public:const int INF = 0x3f3f3f;//int最大值的一半int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n, vector<int>(3, -INF));auto g = f;//初始化f和g表的第一行的第一个元素f[0][0] = -prices[0], g[0][0] = 0;for (int i = 1; i < n; i++){for (int j = 0; j < 3; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);//天数不会越界，因为在这之前f和g表已经初始化了g[i][j] = g[i - 1][j];if (j - 1 >= 0){   //要么j-1交易次数存在，则考虑这种情况，//要么不存在，那么g[i][j]就直接=g[i-1][j]g[i][j] = max(g[i][j], f[i -1][j - 1] + prices[i]);}}}//找到g表最后一行的最大值int ret = 0;for (int i = 0; i < 3; i++)ret = max(g[n - 1][i], ret);return ret;         }
};

9、买卖股票的最佳时机IV

本题跟买卖股票的最佳时机III的分析思路基本一模一样，但是本题多了一个细节问题，即优化时间复杂度

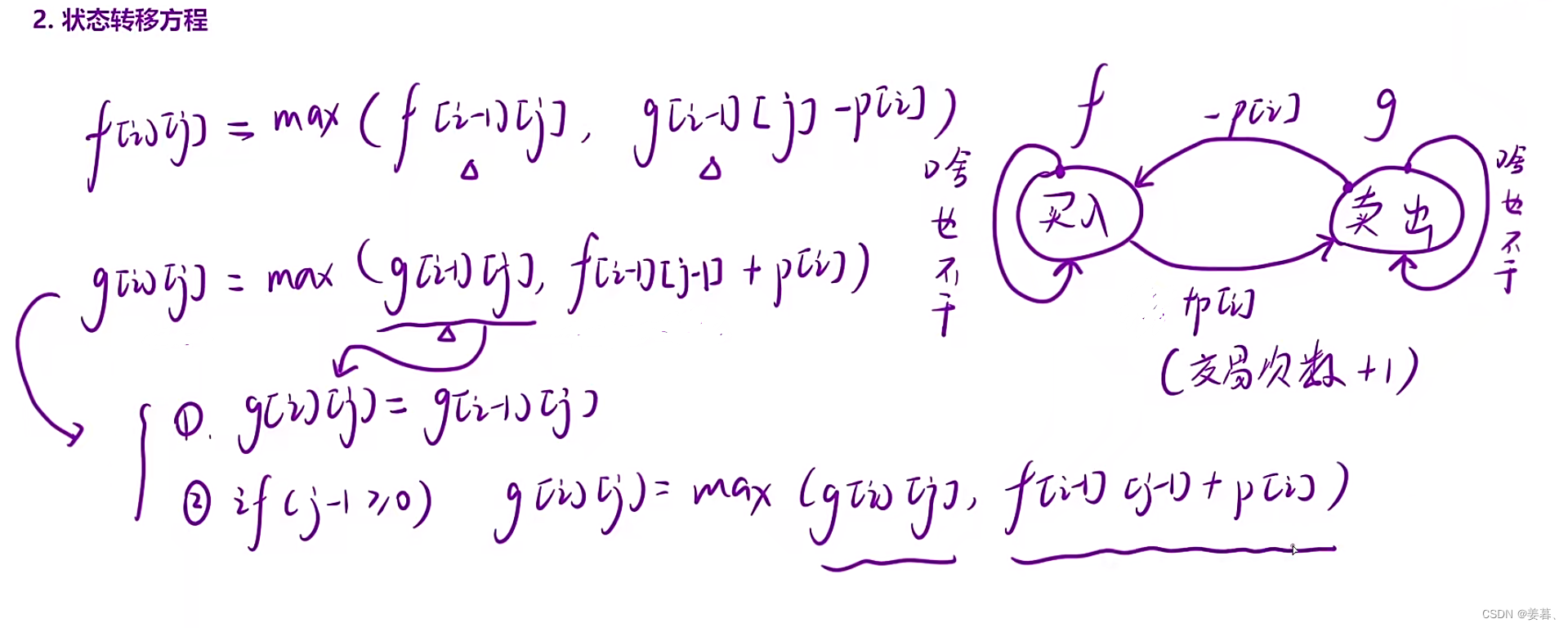
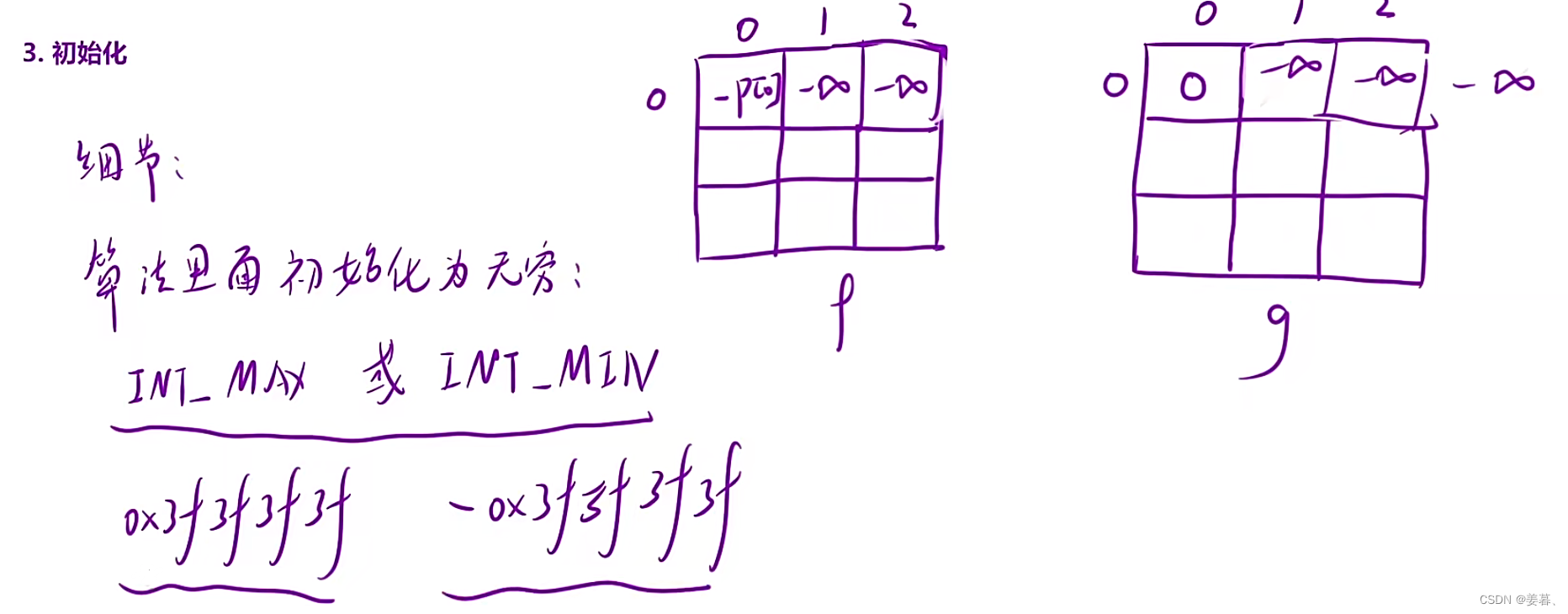
class Solution {
public:const int INF = 0x3f3f3f3f;int maxProfit(int k, vector<int>& prices) {int n = prices.size();k = min(k, n / 2);//处理细节问题vector<vector<int>> f(n, vector<int>(k + 1, -INF));auto g = f;f[0][0] = -prices[0], g[0][0] = 0;for (int i = 1; i < n; i++){//因为第一行已经初始化了，所以i从1开始for (int j = 0; j <= k; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if (j - 1 >= 0)g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);}}int ret = 0;for (int i = 0; i <= k; i++)ret = max(ret, g[n - 1][i]);return ret;}
};