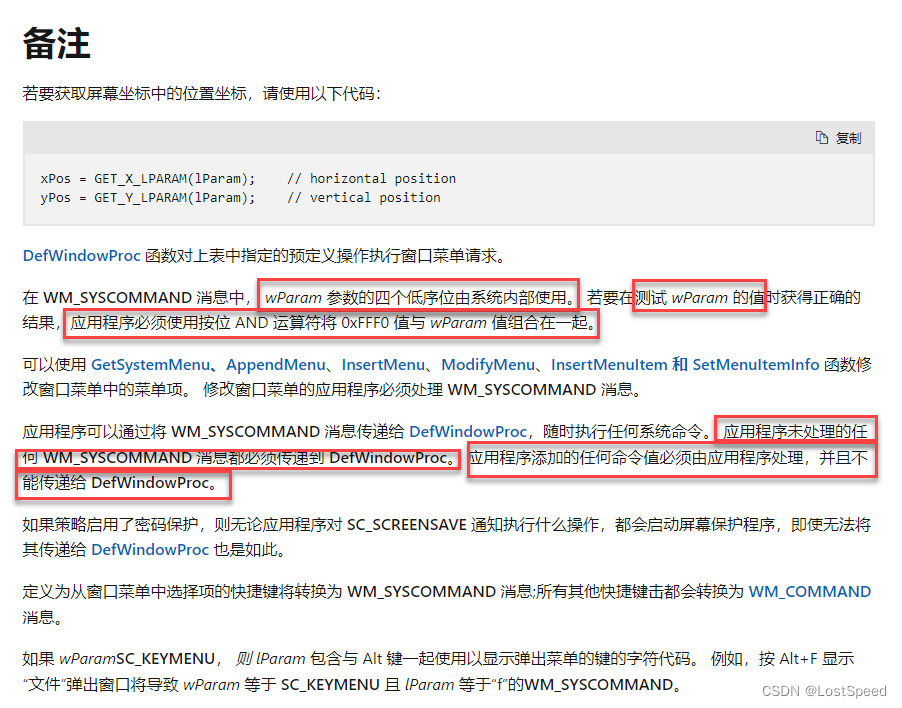
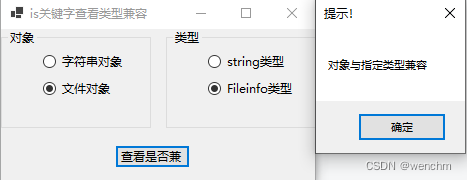
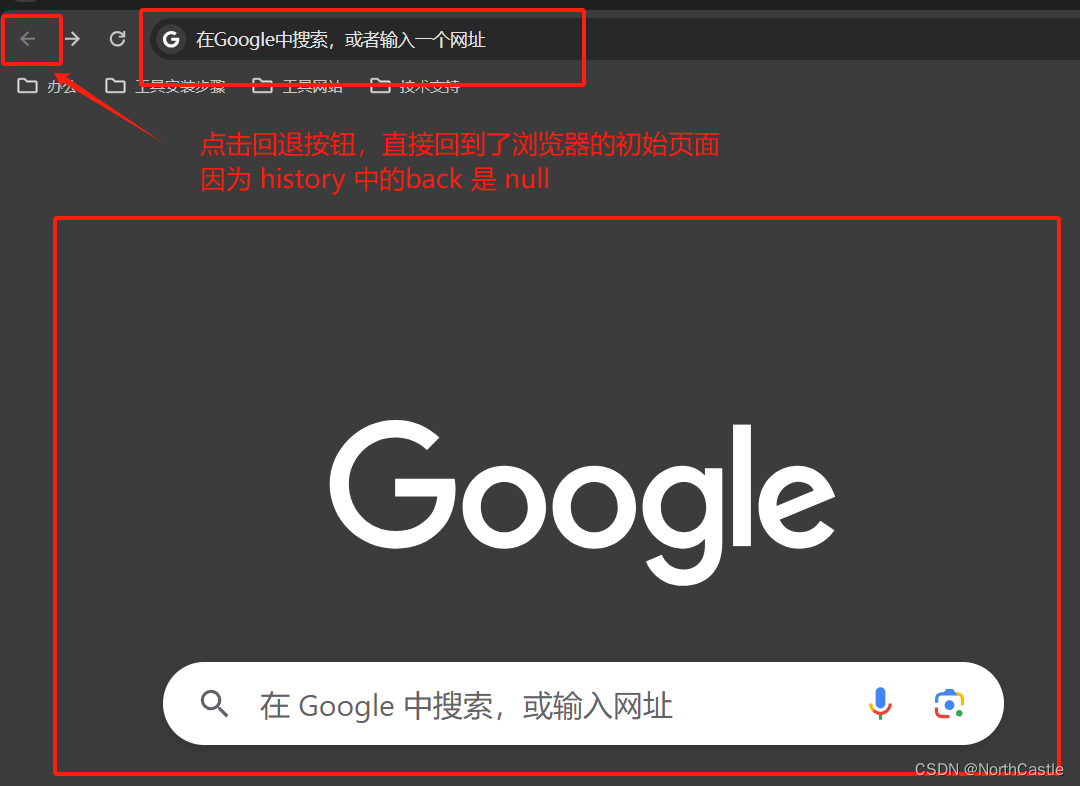
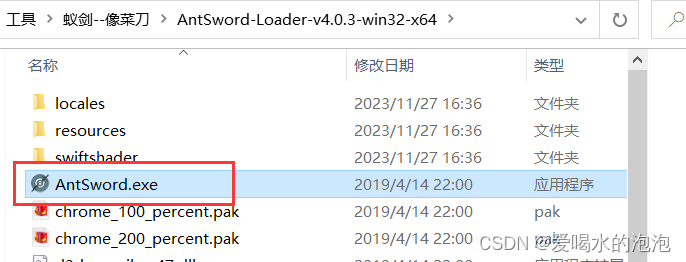
链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台

代码:
class Solution {int[]counts; //用来存储结果int[]index; //用来绑定数据和原下标int[]helpNums; //用于辅助排序 nums 数组int[]helpIndex; //用于辅助排序 index 数组public List<Integer> countSmaller(int[] nums) {List<Integer> list=new ArrayList<>();int length=nums.length;counts=new int[length];index=new int[length];helpNums=new int[length];helpIndex=new int[length];//初始化 index 数组for(int i=0;i<length;i++){index[i]=i;}mergeSort(nums,0,length-1);for(int count:counts){list.add(count);}return list;}//统计 nums 数组中 left ~ right 区间中的逆序对,将统计的数据保存到 counts 中public void mergeSort(int[] nums,int left,int right){//递归出口if(left>=right){return;}//int mid=(right-left)/2+left; //获取中点int mid=(left+right)/2;mergeSort(nums,left,mid); //统计左区间的所有逆序对mergeSort(nums,mid+1,right); //统计右区间的所有逆序对//统计左边一个数据,右边一个数据构成的逆序对int cur1=left,cur2=mid+1,i=0;while(cur1<=mid&&cur2<=right){//统计逆序对if(nums[cur1]>nums[cur2]){counts[index[cur1]]+=right-cur2+1;//将 nums 数组和 index 数组同步修改helpNums[i]=nums[cur1];helpIndex[i++]=index[cur1++];}else{helpNums[i]=nums[cur2];helpIndex[i++]=index[cur2++];}}//处理没有遍历到的数据while(cur1<=mid){helpNums[i]=nums[cur1];helpIndex[i++]=index[cur1++];}while(cur2<=right){helpNums[i]=nums[cur2];helpIndex[i++]=index[cur2++];}//用辅助数组中的数据去代替原数组中的数据for(int j=left;j<=right;j++){nums[j]=helpNums[j-left];index[j]=helpIndex[j-left];}}
}题解:
本题和博主写过的另一题的解法几乎一样,推荐看leetcode LCR 170. 交易逆序对的总数(hard)【小林优质解法】
首先我们来分析一下题意,题目要求我们统计每个数据右边有多少数据小于当前数据,还是比较好理解的,学过线性代数的同学都知道,对于 5,2 这种左边大于右边的数,我们称之为逆序对,所以题目就是要求我们统计数组中每个数据可以组成的逆序对个数
这道题很容易想出暴力解法,就是遍历出数组中所有两个数的组合,判断其中有多少逆序对即可,但时间复杂度为 O(n^2),是比较糟糕的,在本题中会超时
现在博主来介绍如何通过归并排序来解决该题,博主就默认大家是很理解归并排序的,要是不理解一定要先理解了归并排序才能看懂下面的内容,推荐看归并排序(递归)
题目要求统计逆序对个数,我们可以将数组分为左右两个区间,先统计左区间的逆序对个数 A,再统计右区间的逆序对个数 B,最后统计左区间取一个数据,右区间取一个数据组成的逆序对的个数 C,通过 A+B+C 便能得到数组中所有的逆序对个数,其中,统计左区间的逆序对个数 A 和右区间的逆序对个数 B 与统计整个数组的逆序对相同,所以是递归操作,于是我们的目光就要集中在统计左区间取一个数据,右区间取一个数据组成的逆序对的个数 C 上
我们统计 C 的个数时是在统计完 A 和 B 之后,根据归并排序的操作,此时已经排序好了左边和右边区间的数据,归并排序按照递减排序,如下图:
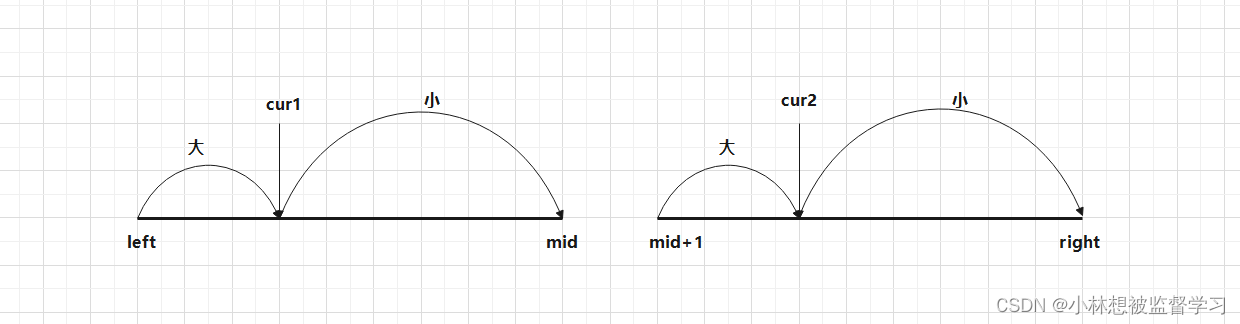
用 cur1 和 cur2 遍历左边和右边的区间,找到其中的逆序对
(1).nums[ cur1 ] > nums[ cur2 ] ,由于在左右区间数据都是递减的,所以 cur2 后面的数据都小于 cur1 指向的数据,此时我们就得到了以 cur1 指向的数据为首的一批逆序对,个数为 right - cur2 + 1 ,要将 nums[ cur1 ] 这个数据的逆序对个数添加到 counts 数组中
现在就有一个问题,counts 数组对应的是 nums[ cur1 ] 这个数据的原下标,因为数据经过了归并排序,顺序已经打乱了,cur1 不是该数据的原下标,我们如何知道 nums[ cur1 ] 这个数据的原下标呢?这里就需要一个小技巧,我们可以在一开始的时候就创建一个数组 index ,index 数组记录了 nums 数组中每个数据的原下标,如下所示:
nums:5 2 6 1
index:0 1 2 3
在这之后,nums 数组如何改变。index 数组就如何改变,这样处理后无论数组中的数据如何改变,我们都能知道每个数据对应的原下标是多少,所以得到 nums[ cur1 ] 这个数据的一批逆序对数目后,要执行 counts[ index[ cur1 ] ] + = right - cur2 + 1 ,在本次递归中 nums[ cur1 ] 这个数据的逆序对就获取完了,让 cur1++
刚好对应归并排序,由于要按照递减排序,所以 nums[ cur1 ] > nums[ cur2 ] ,就将 cur1 指向的数据放到辅助数组 helpNums 中,此时 index 数组中的数据也要对应发生改变,放到辅助数组 helpIndex 中,再让 cur1 ++,
(2).nums[ cur1 ] <= nums[ cur2 ] ,根据递减排序的单调性,因为 cur1 指针右边的数据都小于 cur2 指针指向的数据,所以没有数据能和 nums[ cur2 ] ,构成逆序对,让 cur2 ++,
刚好对应归并排序,由于要按照递减排序,所以 nums[ cur1 ] 《= nums[ cur2 ] ,就将 cur2 指向的数据放到辅助数组 helpNums 中,此时 index 数组中的数据也要对应发生改变,放到辅助数组 helpIndex 中,再让 cur2 ++,