随机森林(Breiman 2001a)(RF)是一种非参数统计方法,需要没有关于响应的协变关系的分布假设。RF是一种强大的、非线性的技术,通过拟合一组树来稳定预测精度模型估计。随机生存森林(RSF)(Ishwaran和Kogalur,2007;Ishwaraan,Kogalur、Blackstone和Lauer(2008)是Breimans射频技术的延伸从而降低了对时间到事件数据的有效非参数分析。
R语言随机森林进行生存分析需要使用到randomForestSRC包,是对Breimans随机森林的统一处理用于生存、回归和分类问题。randomForestSRC包还有一个用于做图的ggRandomForests包,搭配使用,今天咱们来介绍一下怎么使用randomForestSRC包进行随机森林生存分析,内容有点多,咱们分2章来介绍。
咱们先导入数据和R包
library(ggRandomForests)
library(randomForestSRC)
library(ggplot2)
library("dplyr")
pbc<-read.csv("E:/r/test/pbc2.csv",sep=',',header=TRUE)
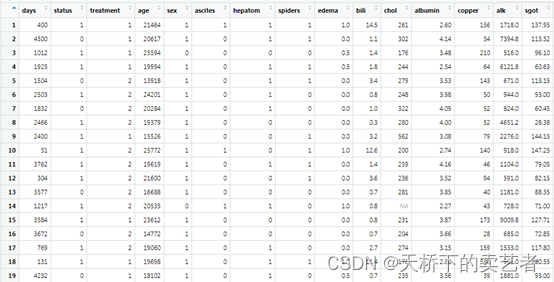
这是一个胆管炎数据(公众号回复:胆管炎数据2,可以获得数据),years:生存时间,status:结局指标,是否死亡,treatment是否DPCA治疗,age年龄,sex性别,ascites是否有腹水,hepatom是否有肝肿大,spiders是否有蜘蛛痣,edema水肿的级别,bili胆红素,chol胆固醇,albumin白蛋白,copper尿酮,alk碱性磷酸酶,sgot:SGOT评分,trig甘油三酯,platelet血小板,prothrombin凝血酶时间,stage组织学分型
我们对数据处理一下,把treatment这个变量变成因子
pbc$treatment<-factor(pbc$treatment)
接下来咱们把数据分成两组,有treatment数据的为测试组,treatment数据缺失的为对照组。
pbc.trial <- pbc %>% filter(!is.na(treatment))
pbc.test <- pbc %>% filter(is.na(treatment))
我们先用生存分析做一遍,等下可以和随机森林进行比较,接下来我们用gg_survival对测试组生成生存分析的数据,这个函数挺方便使用的,生成了生存分析的详尽数据
gg_dta <-gg_survival(interval = "years",censor = "status",by = "treatment",data = pbc.trial,conf.int = 0.95)
绘图
plot(gg_dta) +labs(y = "Survival Probability", x = "Observation Time (years)",color = "Treatment", fill = "Treatment") +theme(legend.position = c(0.2, 0.2)) +coord_cartesian(y = c(0, 1.01))
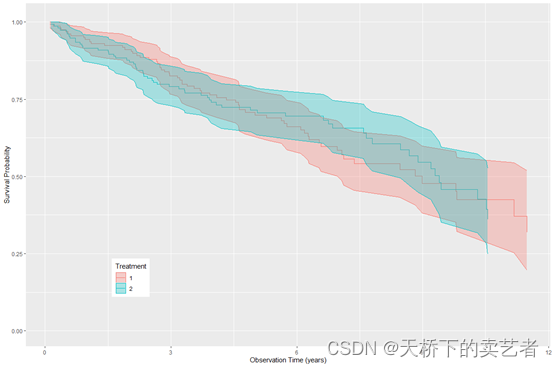
或者绘制成这种累积风险图
plot(gg_dta, type = "cum_haz") +labs(y = "Cumulative Hazard", x = "Observation Time (years)",color = "Treatment", fill = "Treatment") +theme(legend.position = c(0.2, 0.8)) +coord_cartesian(ylim = c(-0.02, 1.22))
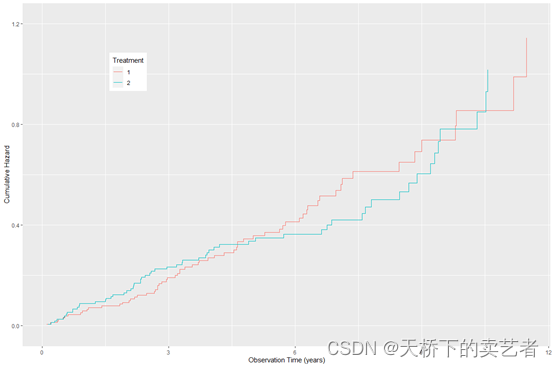
咱们还可以进行断点分层分析,假如咱们对bili这个指标分层4个层(0, 0.8, 1.3, 3.4, 29)
pbc.bili <- pbc.trial
pbc.bili$bili_grp <- cut(pbc.bili$bili, breaks = c(0, 0.8, 1.3, 3.4, 29))
plot(gg_survival(interval = "years", censor = "status", by = "bili_grp",data = pbc.bili), error = "none") +labs(y = "Survival Probability", x = "Observation Time (years)",color = "Bilirubin")
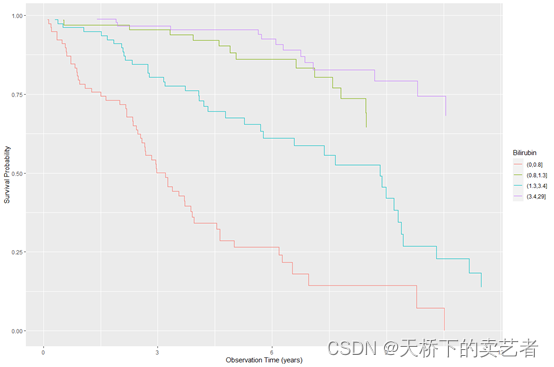
接下来咱们进行随机森林的生存分析,nsplit定义的是随机拆分数,一般默认10次,na.action这里如果选择na.impute就是对缺失数据进行插补,如果选择na.omit就是对缺失数据删除,importance = TRUE这里会计算重要的变量并且进行排序
rfsrc_pbc <- rfsrc(Surv(years, status) ~ ., data = pbc.trial,nsplit = 10, na.action = "na.impute",tree.err = TRUE,importance = TRUE)
查看下基本信息,默认ntree是1000颗数,No. of variables tried at each split: 5这里表示每次都随机取5个变量用于截点。在每个节点,当终端节点包含三个或更少的观测值时停止。Rfsrc函数采用了一个随机logrank分割规则,该规则从nsplit=10中随机选择分割点值。
rfsrc_pbc

程序选择63.2%的样本做估计,剩余36.8%作为袋外数据(OOB)用于测试。gg_error函数对随机林(rfsrc_pbc)对象进行操作以提取错误作为森林中树木数量的函数的估计。
plot(gg_error(rfsrc_pbc))
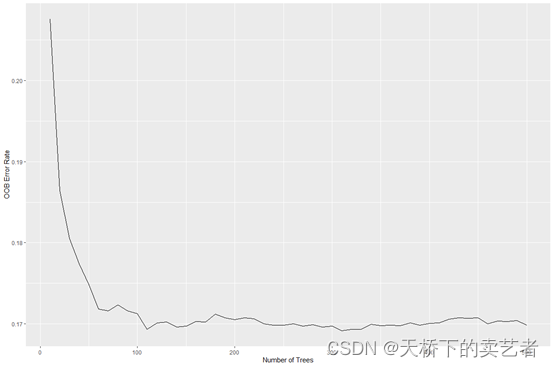
我们可以看到100颗数后,误差已经很稳定了。gg_rfsrc函数可以提取随机森林中袋外数据(OOB)的估计值
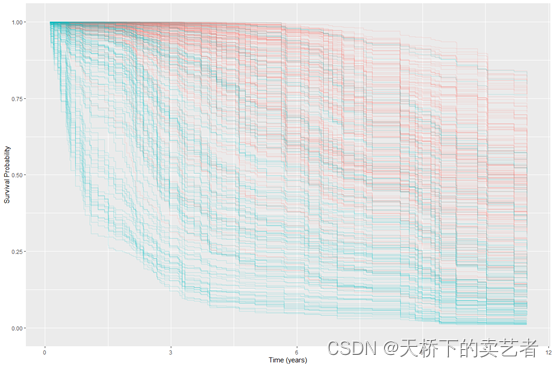
out<- gg_rfsrc(rfsrc_pbc)
进一步绘图
ggRFsrc <- plot(gg_rfsrc(rfsrc_pbc), alpha = 0.2) +theme(legend.position = "none") +labs(y = "Survival Probability", x = "Time (years)") +coord_cartesian(ylim = c(-0.01, 1.01))
ggRFsrc
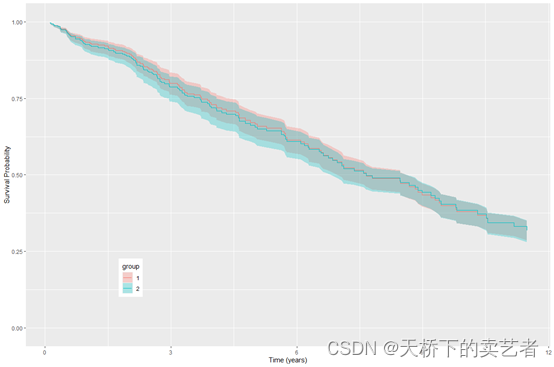
对治疗组和未治疗组进行分类绘图
plot(gg_rfsrc(rfsrc_pbc, by = "treatment")) +theme(legend.position = c(0.2, 0.2)) +labs(y = "Survival Probability", x = "Time (years)") +coord_cartesian(ylim = c(-0.01, 1.01))
使用验证组就行数据评估
rfsrc_pbc_test <- predict(rfsrc_pbc, newdata = pbc.test,na.action = "na.impute",importance = TRUE)
绘图
plot(gg_rfsrc(rfsrc_pbc_test), alpha=.2) +#scale_color_manual(values = strCol) +theme(legend.position = "none") +labs(y = "Survival Probability", x = "Time (years)") +coord_cartesian(ylim = c(-0.01, 1.01))
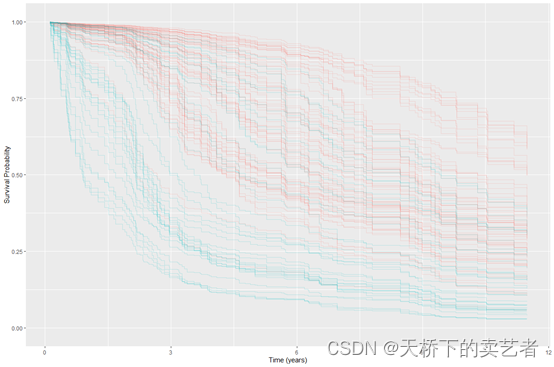
因为咱们选的是treatment缺失的为验证集,这里就不能分组了。
随机林不是一种简约方法,而是使用数据集中所有可用的变量以构建响应预测器。此外,与参数模型不同,随机森林不会要求明确说明协变量对响应的函数形式。因此对于随机森林模型的变量选择,没有明确的p值/显著性检验。相反,RF通过分割规则确定哪些变量对预测有贡献优化,最佳选择分离观察的变量。
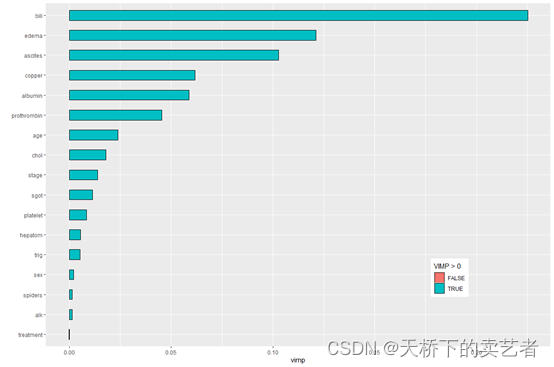
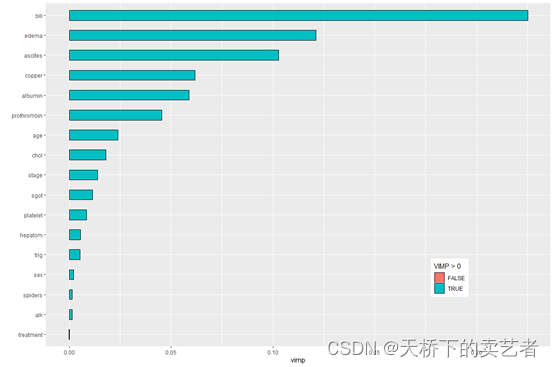
下面来做变量的重要性,VIMP方法使用一种预测误差方法,包括依次对每个变量进行“noising-up”。 由于VIMP是排列前后OOB预测误差的差异VIMP值表示错误指定会降低森林中的预测准确性。VIMP接近零表示该变量对预测准确性没有任何贡献,并且负值表示当变量被错误指定时预测精度提高。
plot(gg_vimp(rfsrc_pbc)) +theme(legend.position = c(0.8, 0.2)) +labs(fill = "VIMP > 0")
本期先介绍到这里,未完待续。