泰勒公式

泰勒公式简单来说就是,可以用一个N次多项式来表示出一个连续可导的函数 f(x)
是一个用函数在某点的信息描述其附近取值的公式

第一步

思考
这是一个sin(x)的图像 用函数在原点的信息描述其附近取值

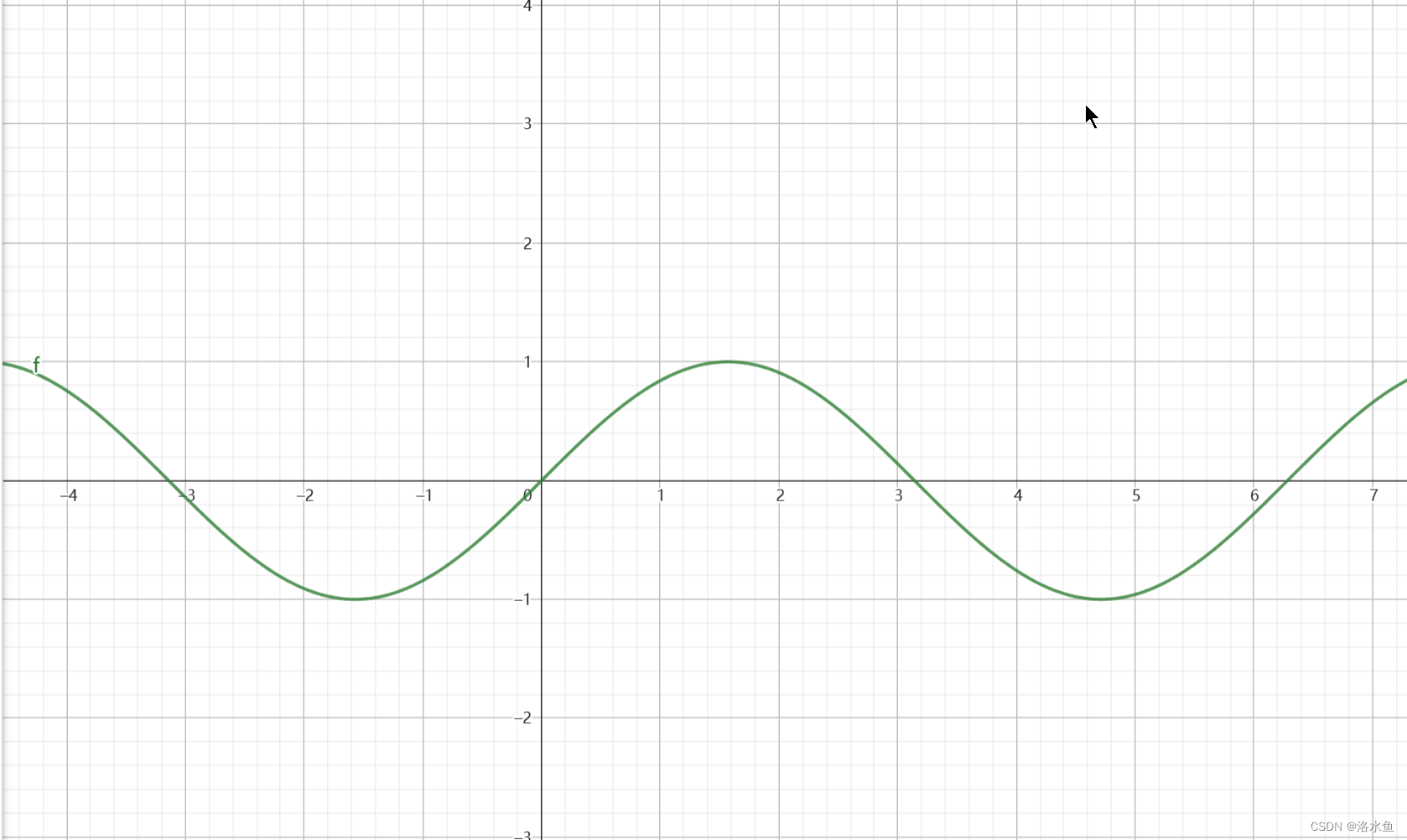
用一阶导数贴合:
直接用切线来贴合就好
画一个点(0,sin(0)除的切线 可以由直线的两点式得 :
$$y=f(0)+f^{\prime }(0)(x-0)$$

$$根据图像我们发现在0附近这个函数和sin(x)很贴合,越靠近0越贴合$$

找个三次函数来贴合:

找个五次函数贴合:

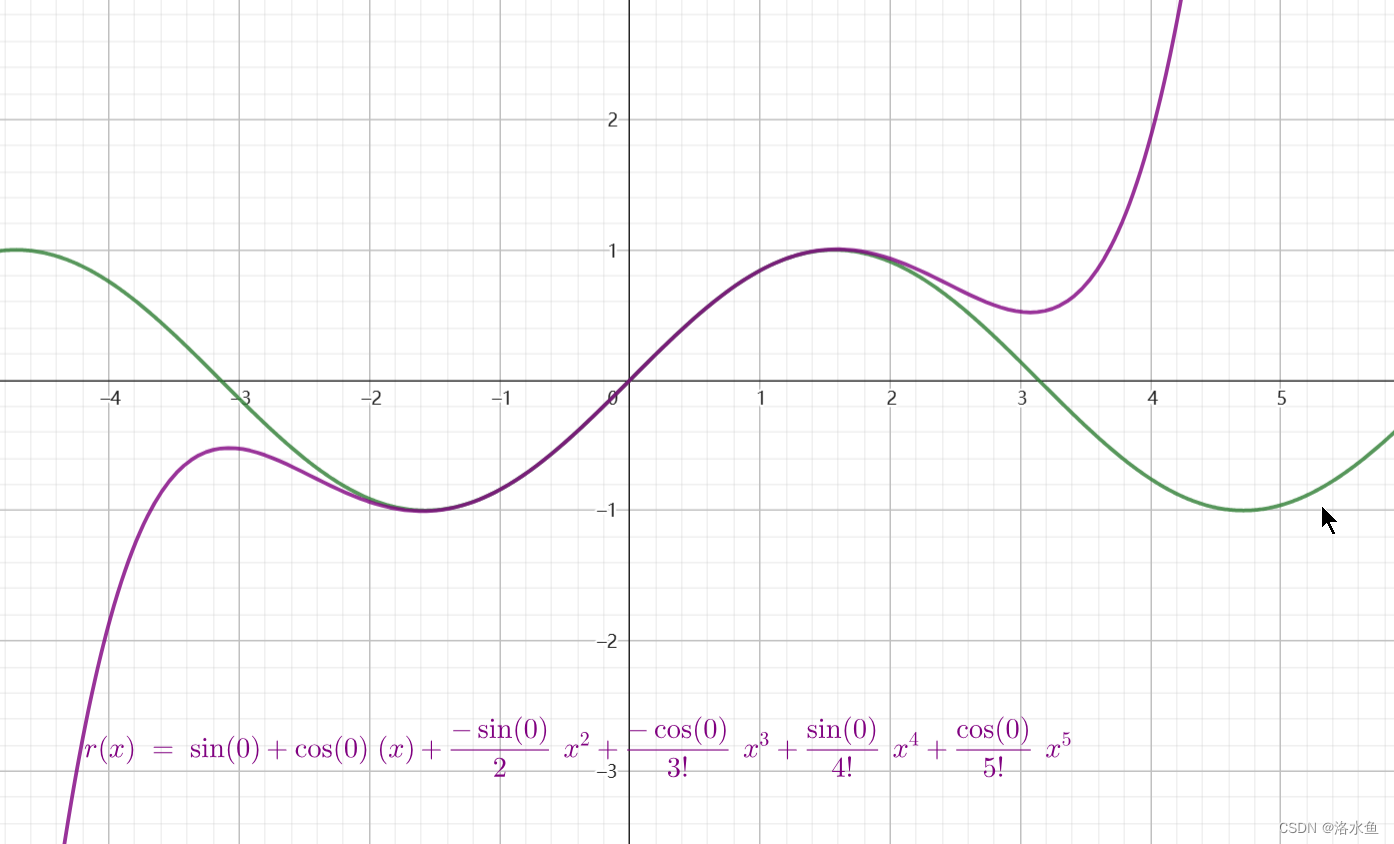
$$我们发现阶数越高越贴合,离0越近越贴合$$

于是我们，大胆假定一个函数可以用N次多项式来进行代替

$$f(x)=C_0+C_{1}x+C_2{x}^2+\dots +C_{N-1}{x}^{N-1}+C_N{x}^N$$

求系数

所以现在变为,我们怎么得到N次多项式的系数

因为我们是由一个点的信息来描述其附近取值,那么我们可以理解为这个点的附近区域的函数段是相同的,那么它们的各阶导数该点的值也是相同的.
举例子:
给定多项式：
$$f(x)=C_0+C_{1}x+C_2{x}^2+C_3{x}^3$$

第一步，令 ( x ) 为零，得到：
$$f(0)=C_0$$

第二步，对 ( f(x) ) 求导，得到一阶导数：
$$f^{\prime }(x)=C_1+2C_{2}x+3C_3{x}^2$$
代入 ( x = 0 )，得到：
$$f^{\prime }(0)=C_1$$

第三步，对 ( f(x) ) 进行二次求导，得到二阶导数：
$$f^{\prime \prime }(x)=2C_2+6C_{3}x$$
代入 ( x = 0 )，得到：
$$f^{\prime \prime }(0)=2C_2$$
$$C_2=\frac{f^{\prime \prime }(0)}{2}$$

第四步，对 ( f(x) ) 进行三次求导，得到三阶导数：
$$f^{\prime \prime \prime }(x)=6C_3$$
代入 ( x = 0 )，得到：
$$f^{\prime \prime \prime }(0)=6C_3$$
$$C_3=\frac{f^{\prime \prime \prime }(0)}{6}$$

然后，你总结得到多项式的泰勒展开式为：
$$f(x)=f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\frac{f^{\prime \prime \prime }(0)}{3!}{x}^3$$

这是一个泰勒展开，适用于充分光滑的函数，通过这个展开式，我们可以近似表示函数在 ( x = 0 ) 附近的行为。

我们通过运算发现
给定函数 f(x)，在 x = a 处的 n 阶泰勒展开式为：

$$P_n(x)=f(a)+f^{\prime }(a)(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\frac{f^{\prime \prime \prime }(a)}{3!}(x-a{)}^3+\dots +\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

$$其中，f^{\prime }(a)表示f(x)在x=a处的一阶导数，f^{\prime \prime }(a)表示二阶导数，以此类推，f^{(n)}(a)表示第n阶导数。$$

通用形式为：

$$P_n(x)=\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k$$

试试不在0展开

在点1处展开:
$$一次多项式:$$

$$三次多项式:$$

$$五次多项式:$$

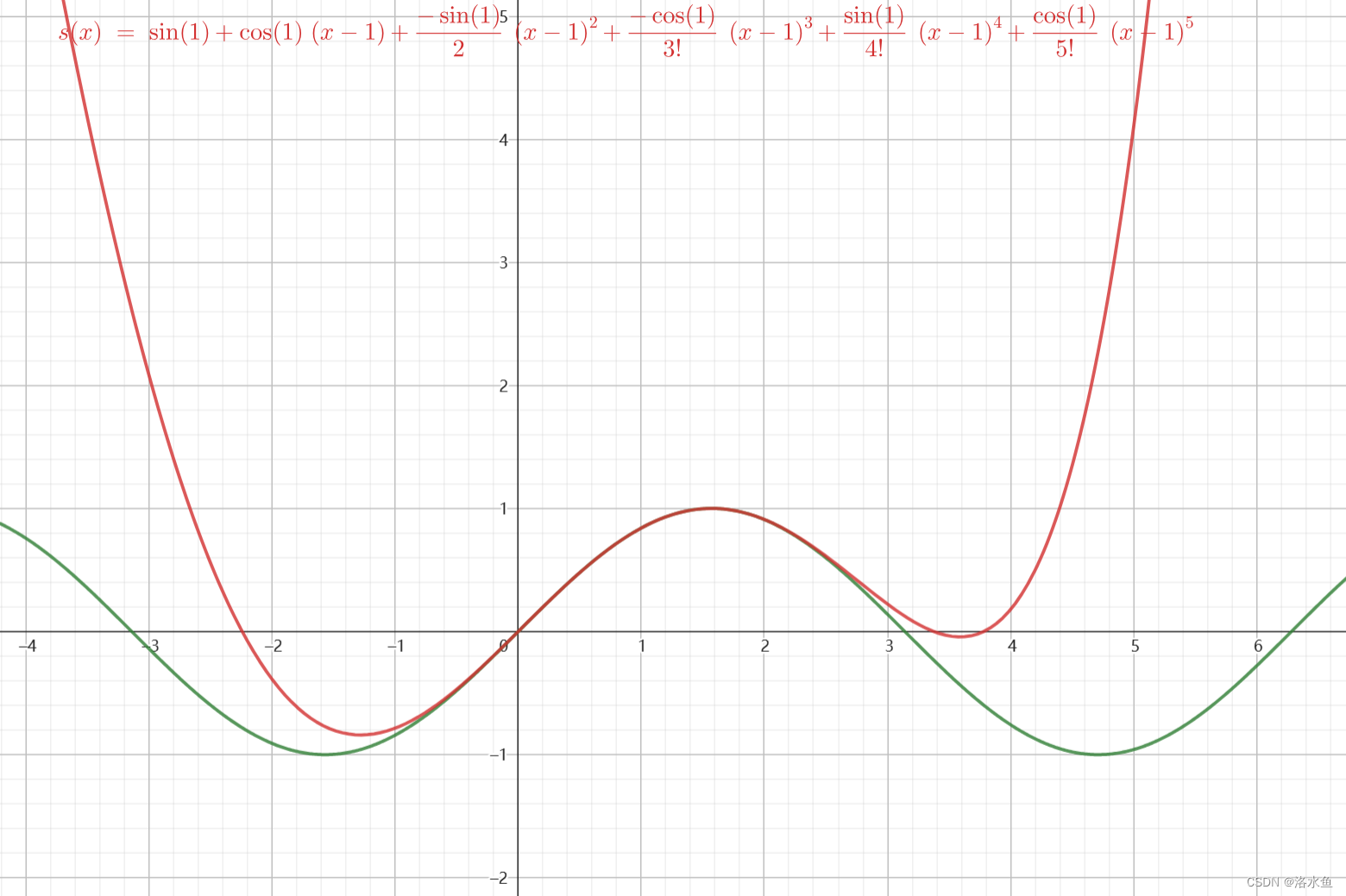
为什么可以表示

1阶导数是描述原函数的变化
2阶导数又是描述一阶导数的变化
所以多次在不断的导是要知道原函数在该点的变化,二阶导又看变化的变化怎么变化…
参考信息:
B站视频【泰勒公式】