约数里面的一个重要性质:一个数的约数都是成对存在的(以sqrt(x)为分界线)
一、求一个数的所有约数---试除法
int x; cin>>x;
int yue[10000]={0},idx=0;
for(int i=1;i<=x/i;i++)
{if(x%i==0){yue[idx++]=i;cout<<i<<" ";}
}for(int i=idx-1;i>=0;i--)
{if(x/yue[i]!=yue[i])cout<<x/yue[i]<<" ";
}二、求一个数的约数的个数---(先对它分解质因数,然后套公式)

const int mod=1e9+7;
map<int,int>h;int x; cin>>x;
for(int i=2;i<=x/i;i++)
{while(x%i==0){x/=i;h[i]++;}
}
if(x>1)h[x]++;long long ans=1;
for(auto i:h)
{ans=ans*(i.second+1)%mod;
}
cout<<ans;三、求一个数的所有约数的和---(先对它分解质因数,然后套公式)
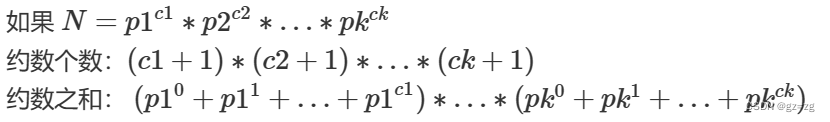
const int mod=1e9+7;
map<int,int>h;int x; cin>>x;
for(int i=2;i<=x/i;i++)
{while(x%i==0){x/=i;h[i]++;}
}
if(x>1)h[x]++;long long ans=1;
for(auto i:h)
{int a=i.first;int b=i.second;long long temp=1;while(b--)temp=(temp*a+1)%mod;ans=ans*temp%mod;
}
cout<<ans;四、求两个正整数的最大公约数---辗转相除法
int gcd(int a,int b)
{if(b==0)return a;else return gcd(b,a%b);
}






![[设计模式 Go实现] 创建型~抽象工厂模式](https://img-blog.csdnimg.cn/direct/00a7138fde214eeaa303e197c3033264.png)
