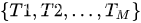一个算法中的经典问题，求最长回文子串问题，其实是可以归于二维动态规划问题。

对于给定的一个字符串中，找到这个字符串中的回文子串，回文子串的概念是从前往后正向的读和从后往前反向的读都是完全相同的字符串。

对这个问题进行分析，首先就是回文子串的最大的特征是把头部和尾部去掉相同数量的字符，中间所留下来的字符串仍然是一个回文子串，举例说明，对于abbacbbcabba这个字符串，其本身是一个回文子串，去掉了头尾相同数量的字符，去掉ab，剩下的bacbbcab还仍是回文子串，或者再在此基础上继续去掉字符，cbbc仍然是回文子串。

而通过回文子串的这个特征，子结构仍为回文子串，即可以定义一个二维数组来表示当前字符串的两位之间是否是回文子串，初始化二维数组的时候默认对角线上的数据是True，其实的地方默认是False。初始化代码如下：

dp=[] 
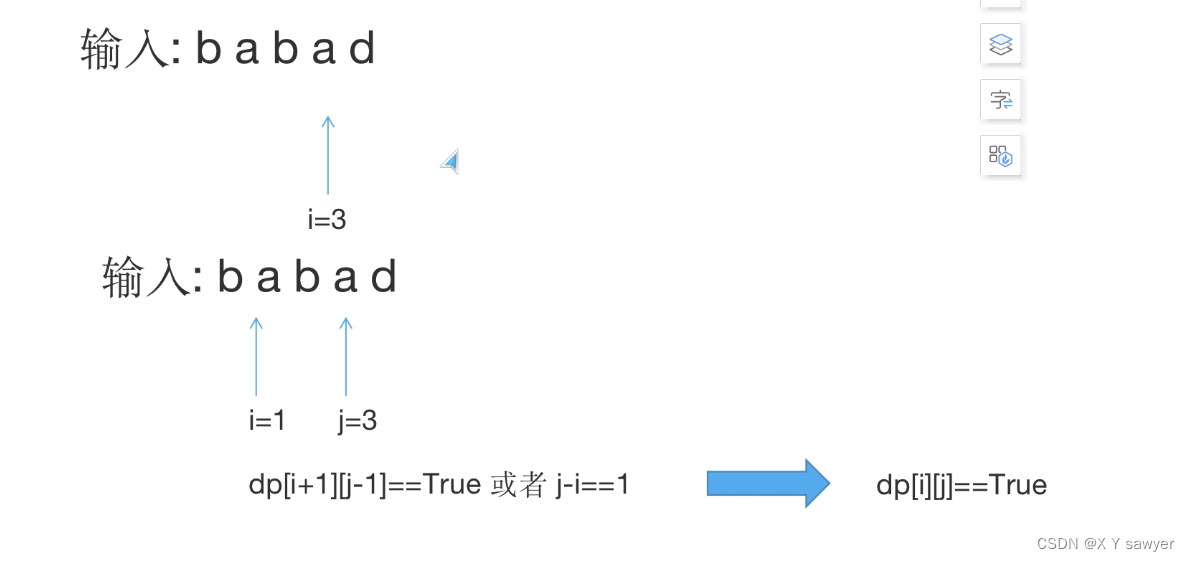
for i in range(len(stringS)):dp.append((False)*len(s)) dp[i][i]=True

然后就是针对解决这个问题，分析得到该问题的递推关系是，当在判断出stringS[i]=stringS[j]，机选判断dp[i-1][j+1]是否是回文串，如果是，那stringS[i]到stringS[j]的子串就是回文串，更新dp[i][j]=True。

由于在判断第i-j位之间是不是回文串之前，需要保证第i+1位到第j-1位是不是回文子串，故此在遍历整个字符串的过程中需要注意要从后往前进行遍历，可以保证i+1到j-1之间的字符串是回文子串，同时也就可以做到减少重复计算了。

如下为动态规划算法的完整代码：

def longestPalindrome(s):right=left=0dp=[]for i in range(len(s)):dp.append([False]*len(s))dp[i][i]=Truei=len(s)-2while(i>=0):#填充二维数组的过程j=i+1while(j<len(s)):dp[i][j]=s[i]==s[j] and (dp[i+1][j-1] or j-i==1)if(dp[i][j] and right-left<j-i):right=jleft=ij+=1i-=1return s[left:right+1]