Leetcode相关题目:
69. x 的平方根
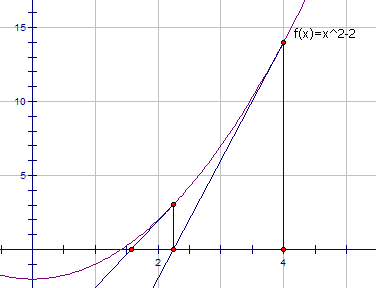
牛顿法 迭代公式:
以求解 a a a 的平方根为例,可转换为求解方程 f ( x ) f(x) f(x)的根。 f ( x ) = x 2 − a f(x)=x^2-a f(x)=x2−a
迭代公式如下: x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1} = x_n - \frac {f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)
代入 f ( x ) f(x) f(x) 得:
x n + 1 = x n − x n 2 − a 2 ∗ x n = x n + a / x n 2 x_{n+1} = x_n - \frac {x_n^2-a}{2*x_n} = \frac{x_n+a/x_n}{2} xn+1=xn−2∗xnxn2−a=2xn+a/xn
停止条件为: ∣ x n + 1 − x n ∣ < ϵ |x_{n+1} - x_n| < \epsilon ∣xn+1−xn∣<ϵ
class MySqrt:"""69. x 的平方根https://leetcode.cn/problems/sqrtx/description/"""def solution1(self, x: int) -> int:"""牛顿迭代法,递归:param x::return:"""self.a = xif x == 0:return 0return int(self.sqrts(x))def sqrts(self, x: float):res = (x + self.a / x) / 2if res == x:return xelse:return self.sqrts(res)def solution2(self, a: int) -> int:"""牛顿法,迭代:param a::return:"""if a == 0:return 0x = float(a)while (x + a / x) / 2 != x:x = (x + a / x) / 2return int(x)def solution3(self, x: int) -> int:"""二分法:param a::return:"""l, r, ans = 0, x, -1while l <= r:mid = l + (r - l) // 2if mid * mid <= x:ans = midl = mid + 1else:r = mid - 1return ans