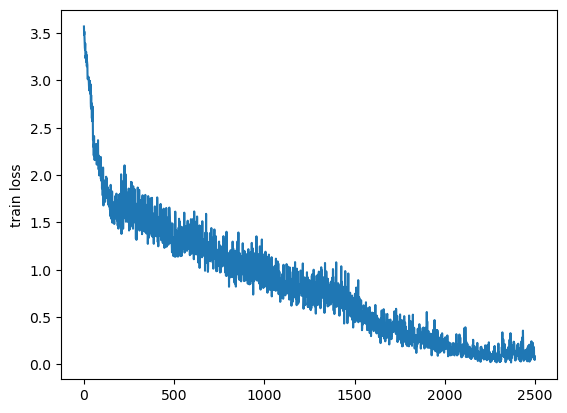
图文证明 罗尔,拉格朗日,柯西
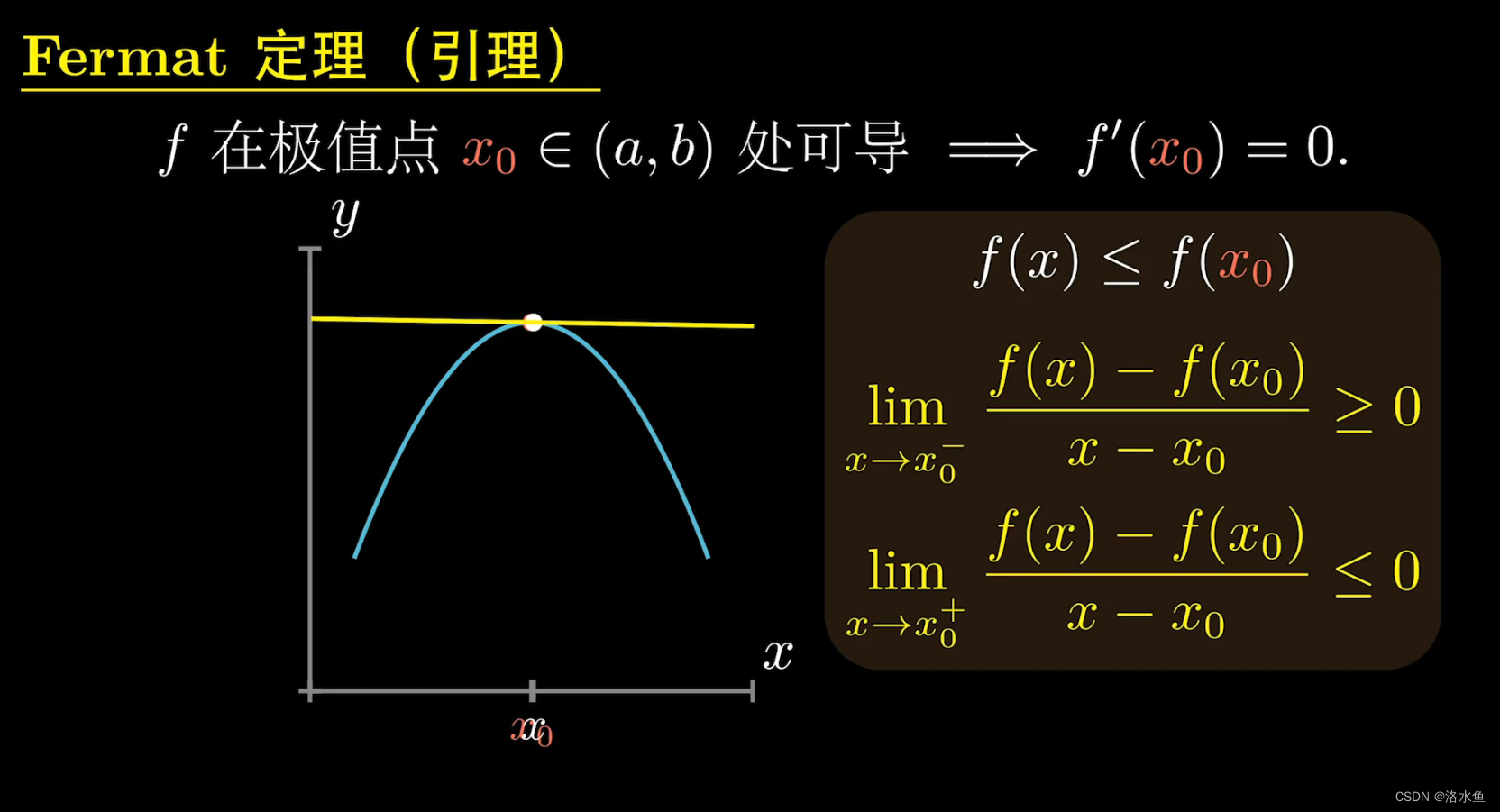
费马引理和罗尔都比较好证,不过多阐述,看图即可:
费马引理:
罗尔定理:

重点来证明拉格朗日和柯西
拉格朗日:

我认为不需要去看l(x)的那一行更好推:
详细的推理过程:
构造 h ( x ) = f ( x ) − l ( x ) , 因为 a , b 两点为交点 , f ( a ) = l ( a ) , f ( b ) = l ( b ) , 构造h(x) = f(x) - l(x), \quad \text{因为} \; a, b \; \text{两点为交点}, \; f(a) = l(a), \; f(b) = l(b), 构造h(x)=f(x)−l(x),因为a,b两点为交点,f(a)=l(a),f(b)=l(b),
所以 h ( a ) = h ( b ) = 0. 根据罗尔定理 , ∃ c ∈ ( a , b ) 使得 h ′ ( ξ ) = 0. \text{所以} \; h(a) = h(b) = 0. \quad \text{根据罗尔定理}, \; \exists \, c \in (a, b) \; \text{使得} \; h'(\xi ) = 0. 所以h(a)=h(b)=0.根据罗尔定理,∃c∈(a,b)使得h′(ξ)=0.
因为 h ( ξ ) = f ( ξ ) − l ( ξ ) , 我们有 h ′ ( ξ ) = f ′ ( ξ ) − l ′ ( ξ ) . 因此 , h ′ ( ξ ) = f ′ ( ξ ) − l ′ ( ξ ) = 0. \text{因为} \; h(\xi ) = f(\xi ) - l(\xi ), \; \text{我们有} \; h'(\xi ) = f'(\xi ) - l'(\xi ). \quad \text{因此}, \; h'(\xi ) = f'(\xi ) - l'(\xi ) = 0. 因为h(ξ)=f(ξ)−l(ξ),我们有h′(ξ)=f′(ξ)−l′(ξ).因此,h′(ξ)=f′(ξ)−l′(ξ)=0.
由此得出 f ′ ( ξ ) = l ′ ( ξ ) . \text{由此得出} \; f'(\xi ) = l'(\xi ). 由此得出f′(ξ)=l′(ξ).
根据两点式得: l ′ ( ξ ) = f ( b ) − f ( a ) b − a \text{根据两点式得:} \; l'(\xi ) = \frac{{f(b)-f(a)}}{{b-a}} 根据两点式得:l′(ξ)=b−af(b)−f(a)
由于已知 f ′ ( ξ ) = l ′ ( ξ ) , 你可以使用这个信息进一步推导出 f ′ ( x ) = l ′ ( x ) = f ( b ) − f ( a ) b − a . \text{由于已知} \; f'(\xi ) = l'(\xi ), \; \text{你可以使用这个信息进一步推导出} \; \ f'(x) = l'(x) = \frac{{f(b)-f(a)}}{{b-a}}. 由于已知f′(ξ)=l′(ξ),你可以使用这个信息进一步推导出 f′(x)=l′(x)=b−af(b)−f(a).
柯西:

给定两个函数 f ( x ) 和 g ( x ) \text{给定两个函数} \; f(x) \; \text{和} \; g(x) \; 给定两个函数f(x)和g(x)
在区间 [ a , b ] 上,其中 f ( x ) ≠ g ( x ) 。根据拉格朗日中值定理,存在 c ∈ ( a , b ) 使得 \text{在区间} \; [a, b] \; \text{上,其中} \; f(x) \neq g(x) \; \text{。根据拉格朗日中值定理,存在} \; c \in (a, b) \; \text{使得} 在区间[a,b]上,其中f(x)=g(x)。根据拉格朗日中值定理,存在c∈(a,b)使得
f ′ ( ξ ) = f ( b ) − f ( a ) b − a , g ′ ( ξ ) = g ( b ) − g ( a ) b − a . f'(\xi ) = \frac{f(b) - f(a)}{b - a}, \quad g'(\xi ) = \frac{g(b) - g(a)}{b - a}. f′(ξ)=b−af(b)−f(a),g′(ξ)=b−ag(b)−g(a).
现在,我们使用换元法,将 f ′ ( ξ ) 的 ( b − a ) 替换为 g ( b ) − g ( a ) g ′ ( ξ ) \text{现在,我们使用换元法,将} \; f'(\xi ) \; \text{的} \; (b - a) \; \text{替换为} \; \frac{g(b) - g(a)}{g'(\xi )} 现在,我们使用换元法,将f′(ξ)的(b−a)替换为g′(ξ)g(b)−g(a)
f ′ ( c ) = f ( b ) − f ( a ) g ( b ) − g ( a ) g ′ ( c ) . f'(c) = \frac{f(b) - f(a)}{\frac{g(b) - g(a)}{g'(c)}}. f′(c)=g′(c)g(b)−g(a)f(b)−f(a).
通过简化得到 f ′ ( c ) = f ( b ) − f ( a ) g ( b ) − g ( a ) ⋅ g ′ ( c ) . \text{通过简化得到} \; f'(c) = \frac{f(b) - f(a)}{g(b) - g(a)} \cdot g'(c). 通过简化得到f′(c)=g(b)−g(a)f(b)−f(a)⋅g′(c).
发现一个看一眼就明了的列子
拉格朗日:如果你一小时跑了5km,你的平均速度就是5km/h。那么在这一小时以内,要么一直保持5km/h,要么一部分比这个速度快,一部分比这个速度慢。在快慢转换的点,你的速度就是5km/h。
柯西:我一小时跑了5km,你一小时跑了20km。要么你的速度一直是我的20/5=4倍,要么你一部分比我四倍还快,一部分比我四倍慢,在这转换的这一点,你的速度是我的四倍。
参考视频:
罗尔、拉格朗日、柯西【中值定理】 证明