信号与线性系统翻转课堂笔记19——连续/离散系统的零极点与稳定性
The Flipped Classroom19 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1)了解连续LTI系统的系统函数零极点对系统时域自由响应模态的影响;
(2)了解离散LTI系统的系统函数零极点对系统时域自由响应模态的影响;
(3,重点和难点)能熟练分析连续LTI系统的系统函数零极点分布对系统频率响应特性的影响;
(4)了解全通系统、最小相移系统的概念及其零极点分布的特点;
(5)了解LTI连续、离散系统为因果系统的充要条件;
(6,重点)理解LTI连续、离散系统稳定的充要条件,能够利用充要条件分析系统的稳定性。
二、问题与解答

(*2)总结连续LTI系统的系统函数极点在s平面的分布特点对系统幅频响应的影响。在此基础上完成习题7.8(可以用MATLAB画幅频响应曲线)。

(*3)设模拟信号为f(t)=cos( 200πt)+sin( 800πt)+cos( 1000πt),想要设计一个连续系统(滤波器),把该信号中角频率为800π的分量滤除掉,另外两个分量保留,如何设置系统函数的零点和极点比较合理?为什么?
(4)全通系统和最小相移系统零极点的分布具有什么特点?分别分析它们为什么会具有全通特性或者最小相移特性。如果一个LTI连续系统的极点都在s右半平面,而零点都在s左半平面,且它们关于虚轴一一镜像对称,该系统是否为全通系统?为什么?
(*5)讨论:①对于连续LTI系统稳定的充要条件有两个表述:一个是“系统冲激响应绝对可积”,另一个是“系统函数的所有极点位于s左半开平面”。这两个充要条件的内涵是否一致?如果不一致,它们之间有何区别?在何种条件下,它们是一致的? ②一个离散LTI系统的极点都在单位圆以内,这个系统在什么情况下不稳定?为什么?
(*6)求解习题7.18、7.19。
1、模拟信号的离散化

T为取样周期。

对于z平面的负实轴
|z|<1,映射到s平面的第二象限
|z|=1,映射到s平面的jω正半轴上
|z|>1,映射到s平面的第一象限
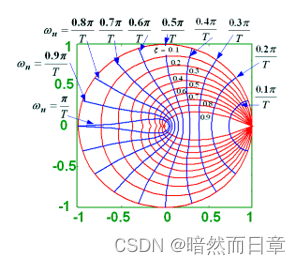
π对应1/2模拟采样频率,不存在大于π的数字频率。
对于单边正弦信号 ,以T=1/8采样并离散化,得到离散信号f(k),则f(k)的z变换F(z)所在z平面的负实轴对应的模拟频率是采样频率的一半即就是4Hz。
2、连续LTI系统函数极点对幅频响应的影响
总结连续LTI系统的系统函数极点在s平面的分布特点对系统幅频响应的影响。在此基础上完成习题7.8(可以用MATLAB画幅频响应曲线)。



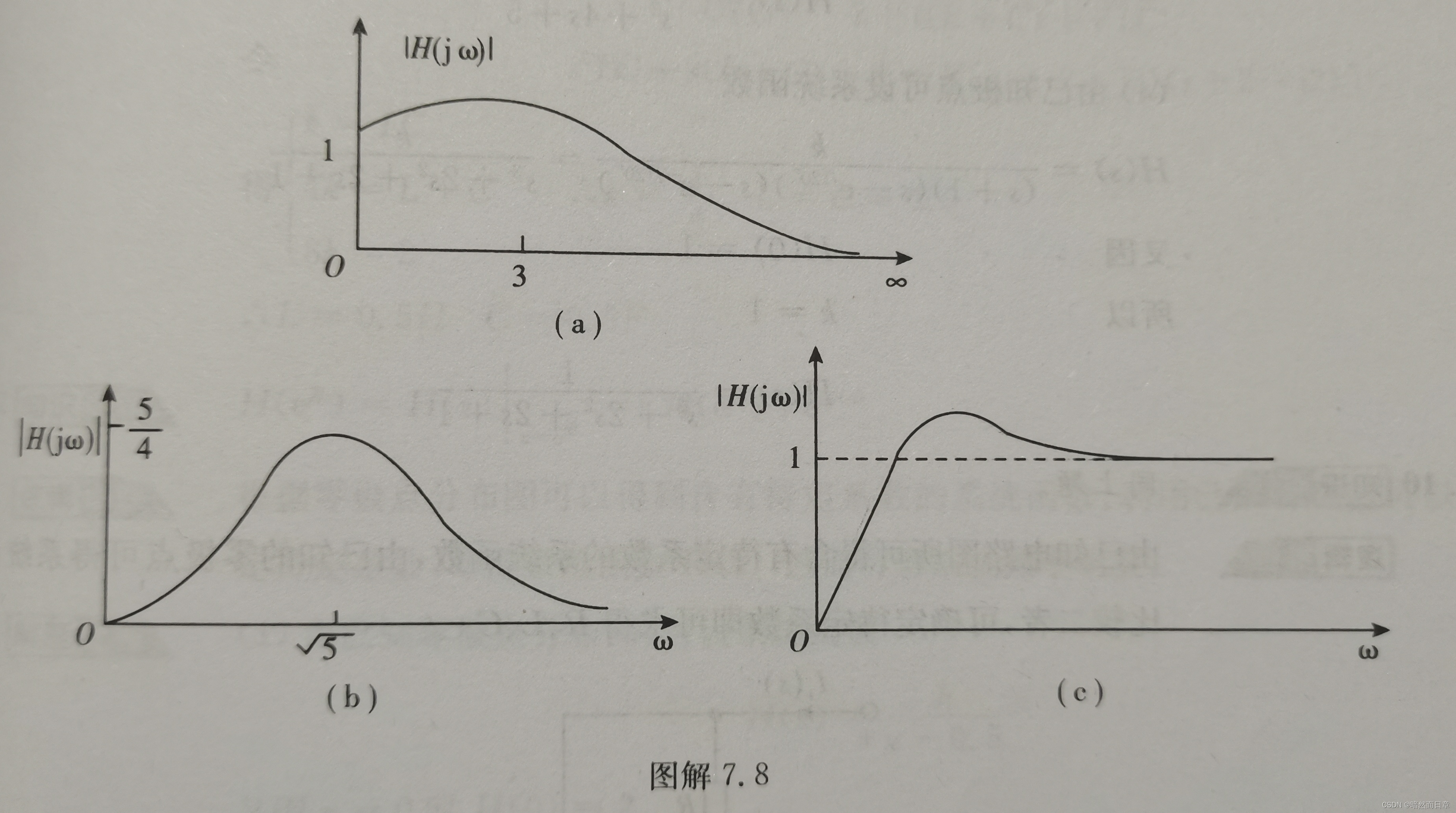
3、设计滤波器滤除特定频率分量
设模拟信号为f(t)=cos(200πt)+sin(800πt)+cos(1000πt),想要设计一个连续系统(滤波器),把该信号中角频率为800π的分量滤除掉,另外两个分量保留,如何设置系统函数的零点和极点比较合理?为什么?


4、全通系统和最小相移系统
全通系统和最小相移系统零极点的分布具有什么特点?分别分析它们为什么会具有全通特性或者最小相移特性。如果一个LTI连续系统的极点都在s右半平面,而零点都在s左半平面,且它们关于虚轴一一镜像对称,该系统是否为全通系统?为什么?
①

全通系统的零、极点分布特点:
1.极点位于左半平面;
2.零点位于右半平面;
3.零点与极点对于虚轴互为镜像。

最小相移系统的零、极点分布特点:
1.极点位于左半平面;
2.系统函数的所有零点均位于左半平面(含虚轴);
3.不同相频特性系统的零点对于虚轴互为镜像。
②分析:
全通系统零点与极点镜像可以使它们到同一频率点的模相同。
最小相移系统(零点与频率点的相角和-极点与频率点的相角和)影响相移特性,零点均位于左半平面使得零点与频率点的相角和最小。
③不是全通系统,全通系统极点位于左半平面;零点位于右半平面;当极点在右半平面,系统是不稳定的。
5、系统稳定的条件
讨论:①对于连续LTI系统稳定的充要条件有两个表述:一个是“系统冲激响应绝对可积”,另一个是“系统函数的所有极点位于s左半开平面”。这两个充要条件的内涵是否一致?如果不一致,它们之间有何区别?在何种条件下,它们是一致的? ②一个离散LTI系统的极点都在单位圆以内,这个系统在什么情况下不稳定?为什么?
①不一致。
“系统冲激响应绝对可积”含义为对于任意的有界输入,系统的零状态响应有界。
“系统函数的所有极点位于s左半开平面”含义为连续LTI系统为因果系统,因为所有极点位于s左半开平面,所以系统冲激响应为衰减的,就会满足绝对可积条件,系统稳定。
“系统冲激响应绝对可积”与“系统函数的所有极点位于s左半开平面”在系统为因果系统时内涵是一致的。
②非因果系统不稳定。在 序列指数衰减,绝对可积,但在左半平面影响下,系统不稳定。
6、判断系统是否稳定实例
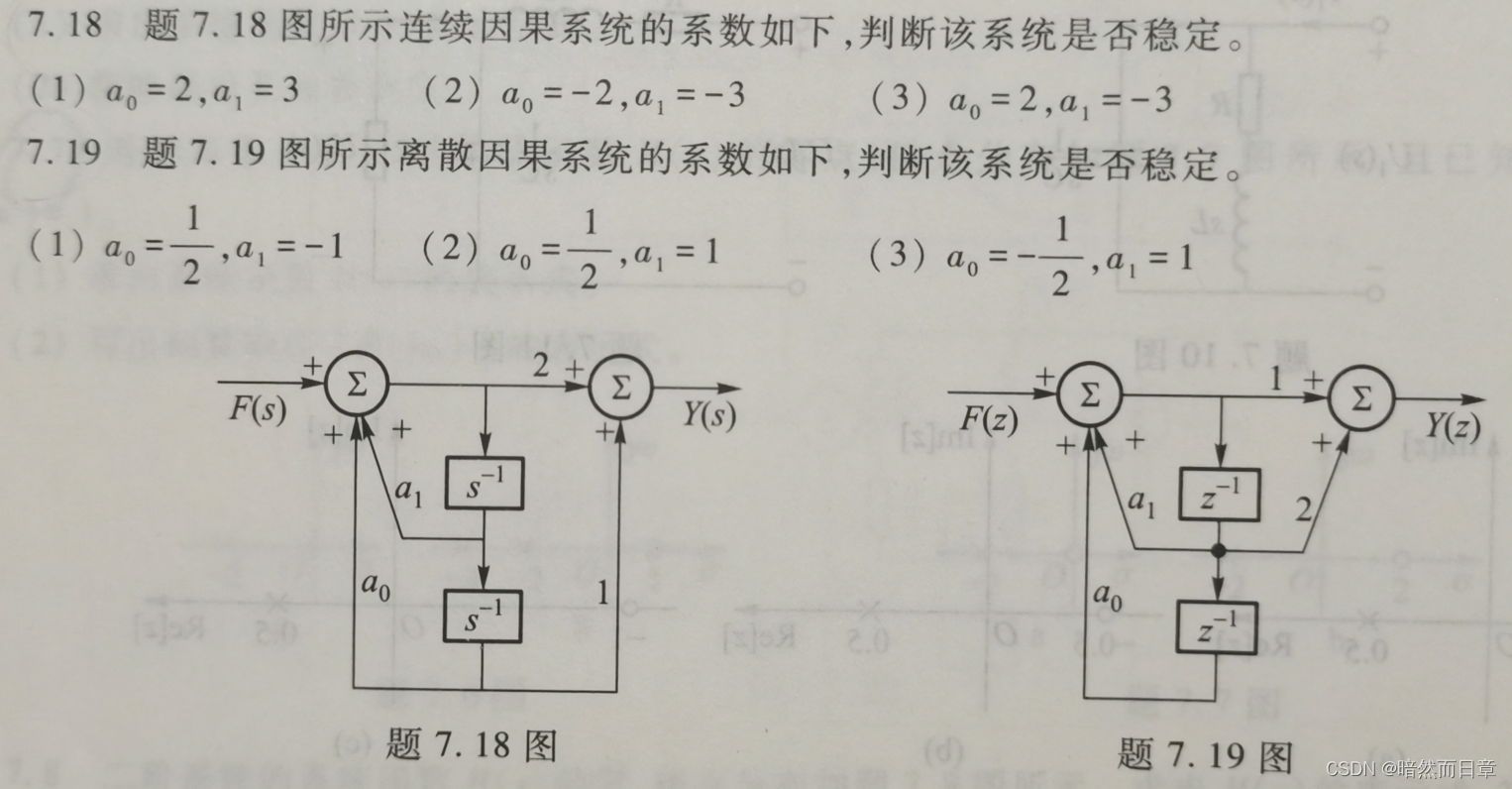
求解习题7.18、7.19。

7.18

7.19