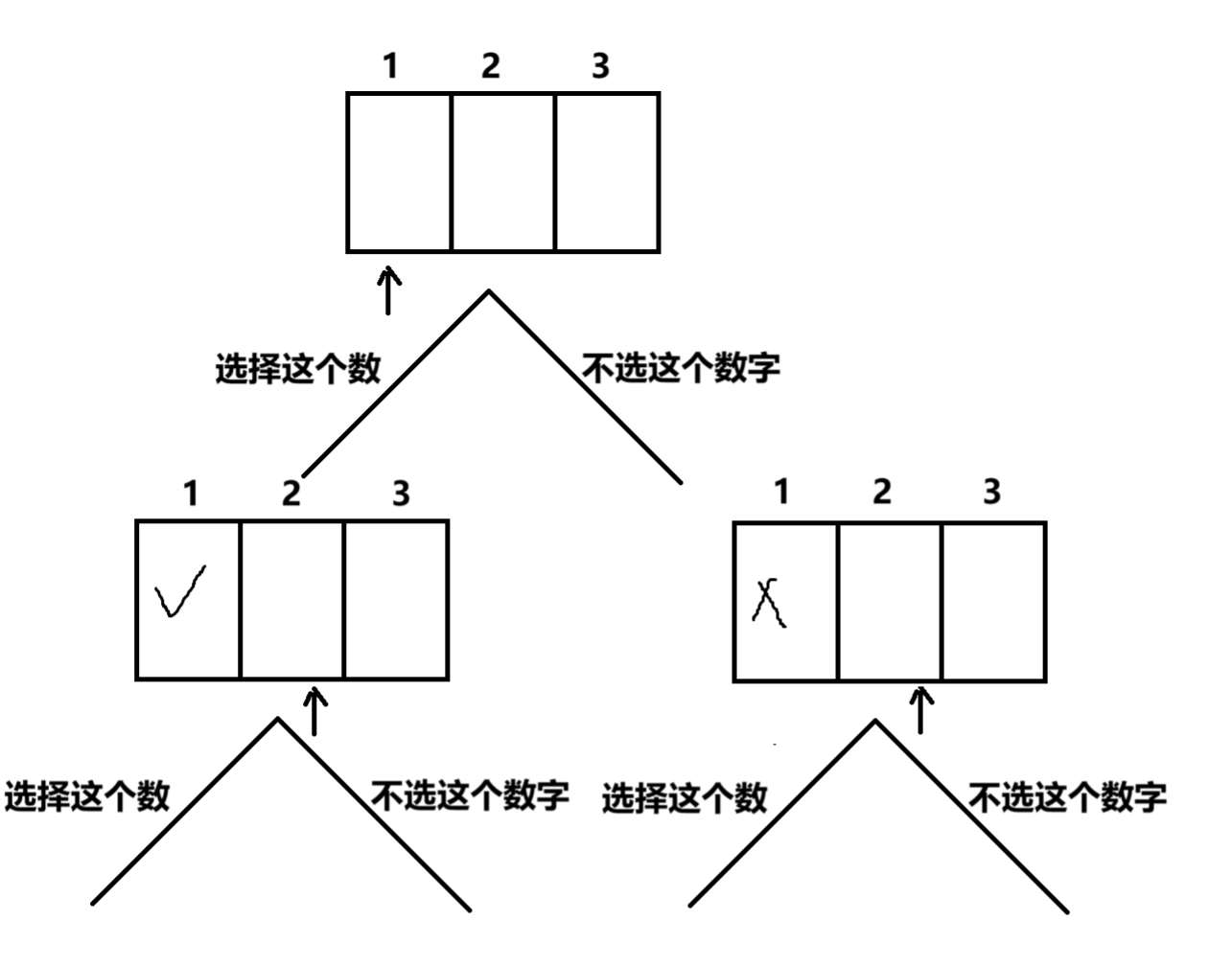
392.判断子序列
第一种思路是双指针,详细代码如下:
class Solution {
public:bool isSubsequence(string s, string t) {//双指针if(s.empty()&&t.empty()) return true;int i=0,j=0;while(i<t.size()){if(s[j]==t[i]) j++;if(j==s.size()) return true;i++;}return false;}
};按照动态规划的思路:
这道题和最长公共子序列(不连续)几乎相同,找的是两个字符的最长公共部分,但是这道题是s已经是子序列了,所以不相等的时候s序列不需要进行删除,只需要删除s的元素,如果最长公共部分长度和s的长度相同,则返回true,否则返回false,不再详细进行动态规划的分析。
详细代码如下:
class Solution {
public:bool isSubsequence(string s, string t) {if(s.empty()&&t.empty()) return true;vector<vector<int>>dp(s.size()+1,vector<int>(t.size()+1,0));for(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=dp[i][j-1];}}if(dp[s.size()][t.size()]==s.size()) return true;else return false;}
};115.不同的子序列
这道题的需要延续判断子序列的思路:
dp[i][j]:以s[i-1]结尾的t[j-1]结尾的子序列个数;
递推:
这一类问题,基本是要分析两种情况
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要 dp[i-1][j-1]。一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
初始化:
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。
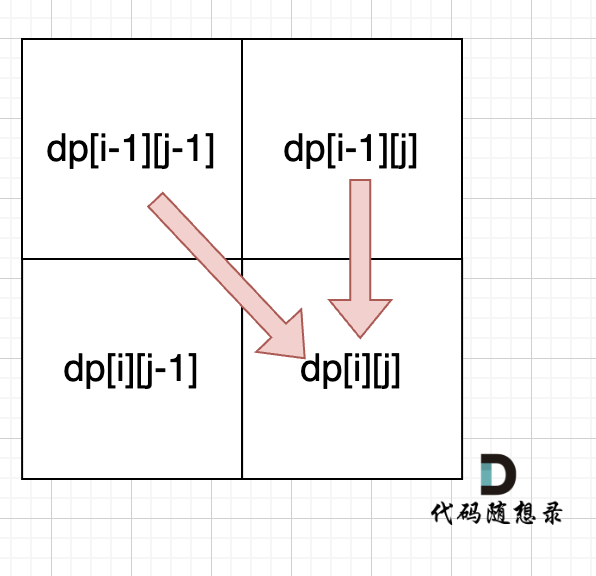
每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
dp[i][0]表示什么呢?
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
再来看dp[0][j],dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。
那么dp[0][j]一定都是0,s如论如何也变成不了t。
最后就要看一个特殊位置了,即:dp[0][0] 应该是多少。
dp[0][0]应该是1,空字符串s,可以删除0个元素,变成空字符串t。
详细代码如下:
class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>>dp(s.size()+1,vector<uint64_t>(t.size()+1,0));for(int i=0;i<=s.size();i++) dp[i][0]=1;for(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+dp[i-1][j]; //使用s[i-1]和不else dp[i][j]=dp[i-1][j];}}return dp[s.size()][t.size()];}
};