椭圆曲线加密 Ellipse Curve Cryptography
椭圆曲线上的离散对数问题 Ellipse Curve Discrete logarithm Problem

椭圆曲线
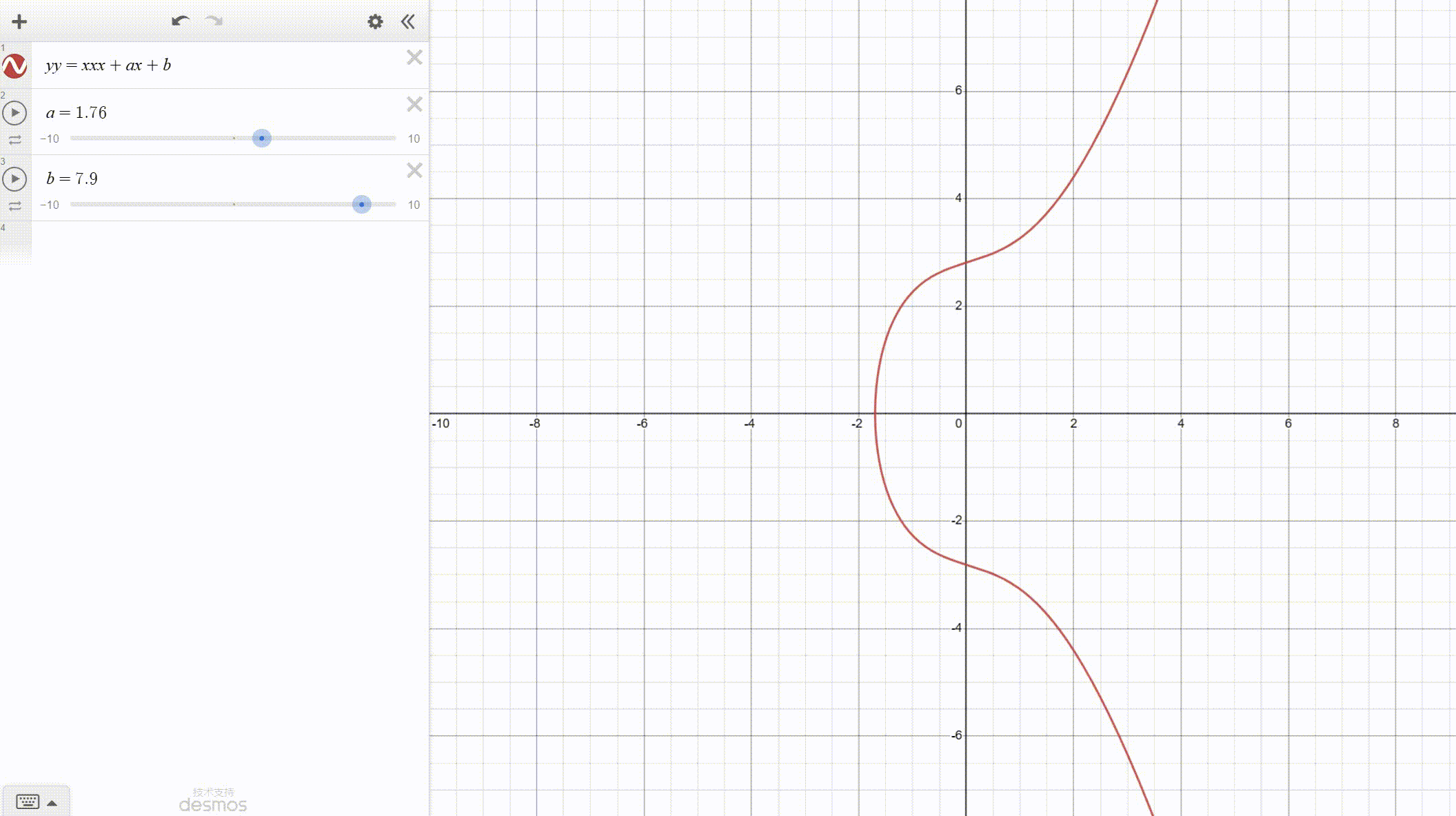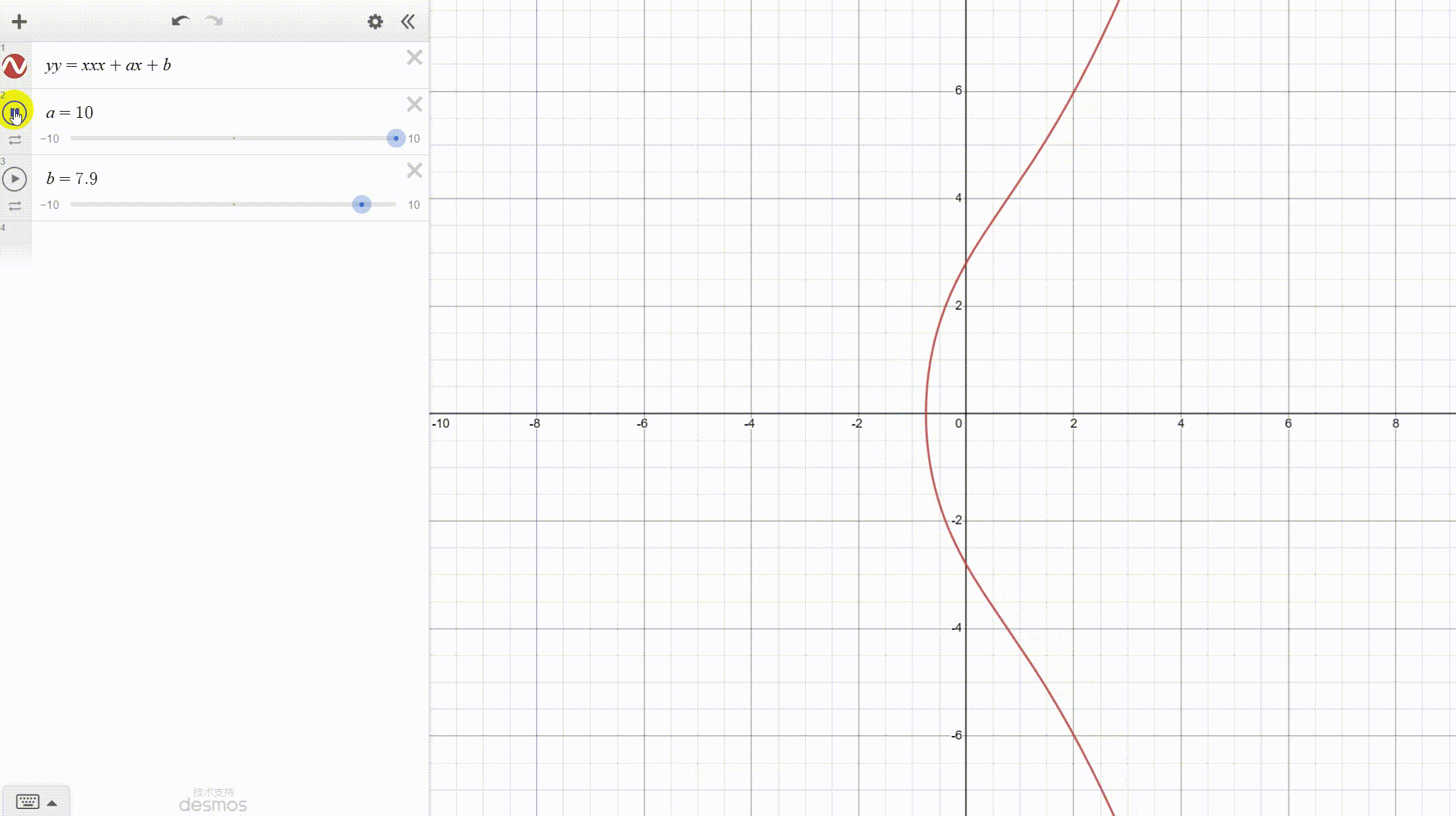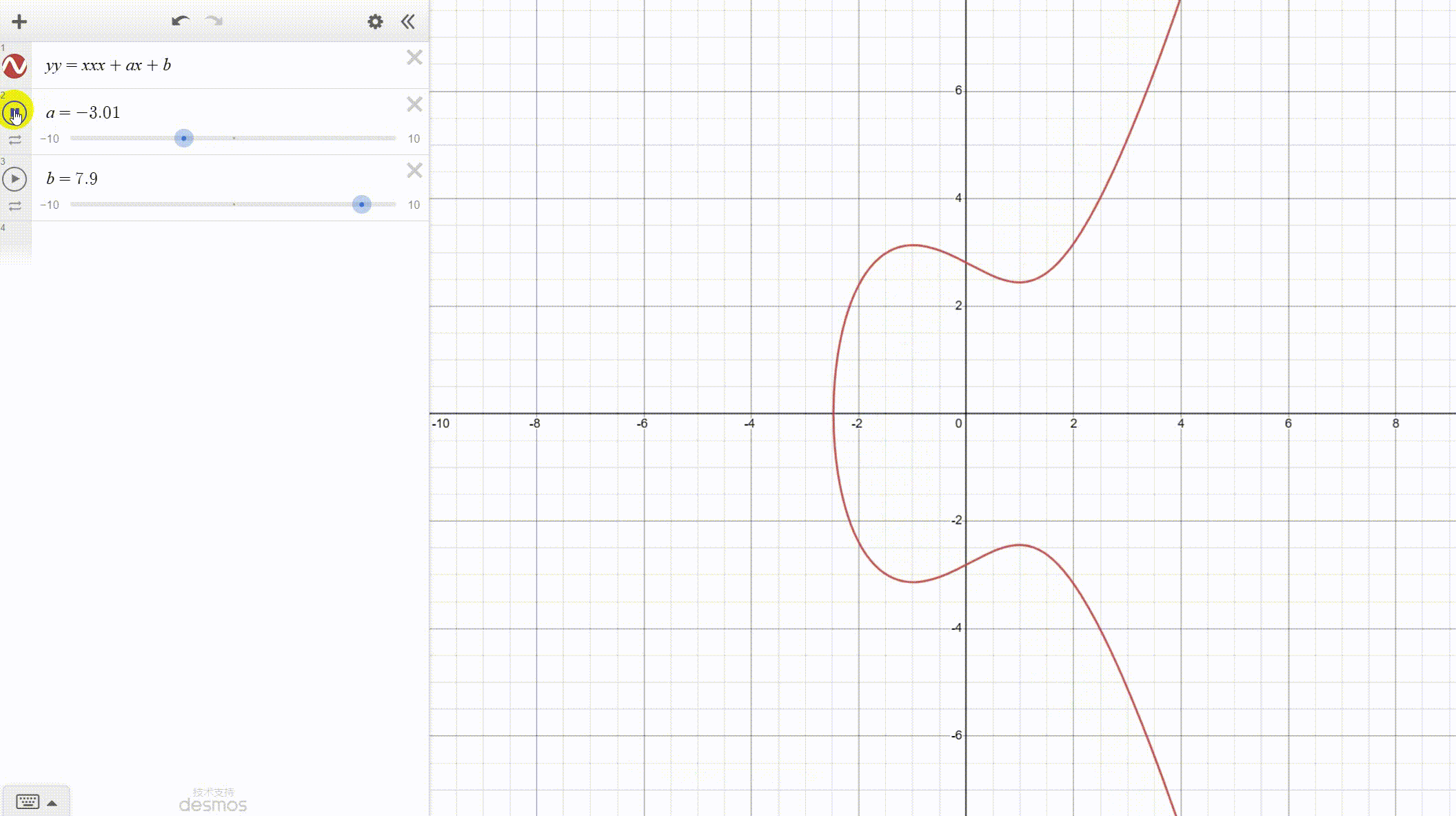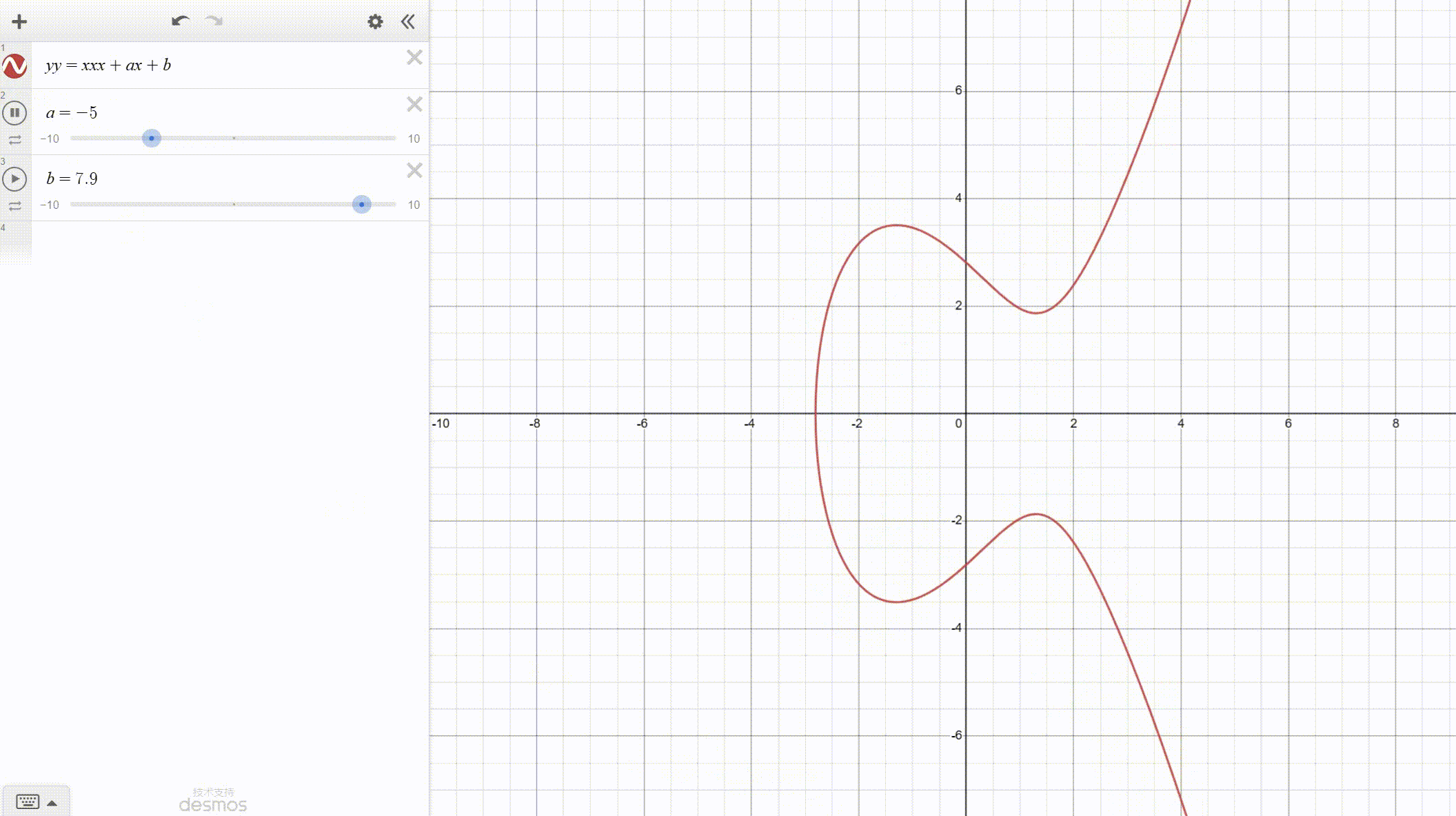
注意积分公式的分母,椭圆曲线由此得名。这种曲线和椭圆一点不像。

离散对数:
y=g^x mod p,对于给定的g,x,p求y很容易,但已知y,g,p求x困难。难度与RSA中的大数分解难度相同。
椭圆曲线上的离散对数问题:
考虑方程Q=kP,其中(点Q,P属于定义在(a,b)上的模p的椭圆曲线)且k<p。对于给定的k,P,计算Q比较容易,但对于给定的Q,P,计算k困难。
y^2=x^3+9x+17( mod 23),定义椭圆群。
**待续
需要一些数学技巧把明文m映射到在椭圆曲线E上的整数点Pm。可能需要对m进行padding,更糟糕的情况,需要调整椭圆曲线的(a,b)。
目前有椭圆曲线和参考点G(一个在椭圆曲线上的整数点)
用户A选择一个私钥Na(一个足够大的数),并计算公钥Pa=Na*G(椭圆曲线的点加计算)
用户B选择一个私钥Nb(一个足够大的数),并计算公钥Pb=Nb*G(椭圆曲线的点加计算)
加密:
用户A随机选取一个整数k ,计算密文Cm
Cm={kG,Pm+kPb},Pb为用户B的公钥。
解密:
解包Cm,使用用户B的私钥Nb,进行ecc上的点加计算。
(Pm+kPb)-Nb(kG)=Pm+k(Nb*G)-Nb(k*G)=Pm