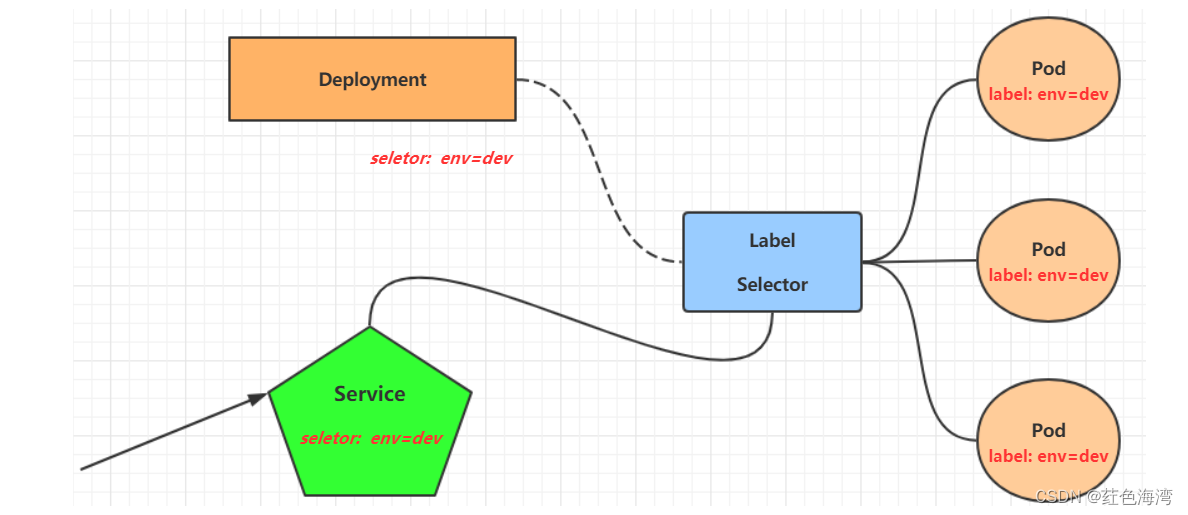
Logistic 回归是一种常用的处理二分类问题的线性模型。采用𝑦 ∈ {0, 1}以符合Logistic回归的描述习惯。

为了解决连续的线性函数不适合进行分类的问题，引入非线性函数𝑔：ℝ𝐷 → (0, 1)来预测类别标签的后验概率𝑝(𝑦 = 1|𝒙)。

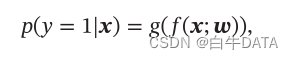1

其中 𝑔(⋅) 通常称为激活函数，其作用是把线性函数的值域从实数区间“挤压”到了(0, 1)之间，可以用来表示概率。在统计文献中，𝑔(⋅)的逆函数𝑔−1(⋅)也称为联系函数（Link Function）。在Logistic回归中，我们使用Logistic函数来作为激活函数．标签𝑦 = 1的后验概率为

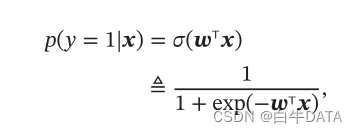2

为简单起见，这里 𝒙 = [𝑥1, ⋯ , 𝑥 𝐷, 1]T 和 𝒘 = [𝑤1, ⋯ , 𝑤𝐷, 𝑏]T 分别为 𝐷 + 1 维的增广特征向量和增广权重向量。

标签𝑦 = 0的后验概率为

3

将公式2进行变换后得到

4

其中 𝑝(𝑦 = 1|𝒙)/𝑝(𝑦 = 0|𝒙)为样本𝒙为正反例后验概率的比值，称为几率（Odds），几率的对数称为对数几率。公式4中等号的左边是线性函数，这样 Logistic 回归可以看作预测值为“标签的对数几率”的线性回归模型。因此，Logistic回归也称为对数几率回归。

图3.4给出了使用线性回归和 Logistic回归来解决一维数据的二分类问题的示例。