针对二维动态规划，还有一个问题就是关于求不同路径的实例，主要是说明在实际应用的场景中，要理解透彻实际问题的真正目的，就可以灵活实现代码编写。

对于求不同路径问题描述，对于一个机器人，处在一个mxn的网格子的最左上端，这个机器人每一次移动只能是向左或者向下移动一个格子，机器人的最终目的是到达网格子的最右下端，要想得到的就是这个机器人总共有多少中方法能够到达最右下端，约束条件是m和n的值不会超过100。

添加图片注释，不超过 140 字（可选）

对照动态规划问题的元素对这个问题进行分析，该问题中的机器人每次只能向下或者向右走一步，那如果这个机器人如果处在网格中的任意一处时，来自的机器人要不就是左侧要不就是来自上侧的网格子，所以对于当前机器人所处的网格子的路径数量，应该是到该格子的上侧格子路径总数和到该格子的左侧格子路径总数的数量之和，同时对于该问题限制了m和n的数量，该问题是可以使用动态规划思路来解决问题的。

添加图片注释，不超过 140 字（可选）

可以将该格子定义为一个二维网格空间，使用一个二维数组来进行表示，对于这个二维数组中的初始状态就是第一行和第一列都是1，这是显而易见的，第一列和第一行都只有一只公路径，到达第一行就只有向右走，到达第一列只有向下走的趋势才能够实现。

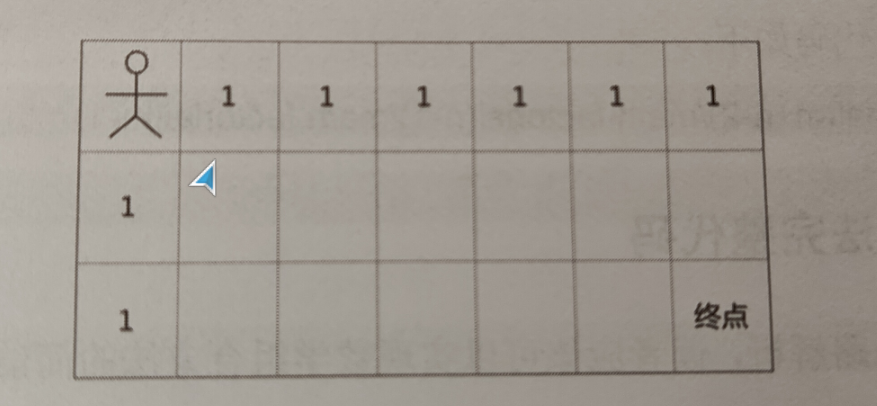
添加图片注释，不超过 140 字（可选）

其他的格子是在遍历过程中，使用递推关系式来进行填充格子的路径数量，也就是当前所在的网格的路径数量应该等于到达这个格子的左侧和上侧的各自的路径数量的总和。最终得到到达终点的格子的数量总和。完整代码如下：

def uniquePaths(self, m, n): dp=[] for i in range(n):#初始化 dp.append([0]*m) for i in range(n): dp[i][0]=1 dp[0]=[1]*m for i in range(1,n): for j in range(1,m): dp[i][j]=dp[i-1][j]+dp[i][j-1] return dp[n-1][m-1]