图像的腐蚀与膨胀
设集合 B B B的反射为 B ^ \hat{B} B^,其定义如下
B ^ = { w ∣ w = − b , b ∈ B } \hat{B}=\begin{Bmatrix}w|w=-b,b\in B\end{Bmatrix} B^={w∣w=−b,b∈B}
设集合 B B B按照点 z = ( z 1 , z 2 ) z=(z_1,z_2) z=(z1,z2)平移得到集合 ( B ) z (B)_z (B)z,其定义如下
( B ) z = { c ∣ c = b + z , b ∈ B } \left(B\right)_{z}=\left\{c\mid c=b+z,b\in B\right\} (B)z={c∣c=b+z,b∈B}
其中操作如下图所示
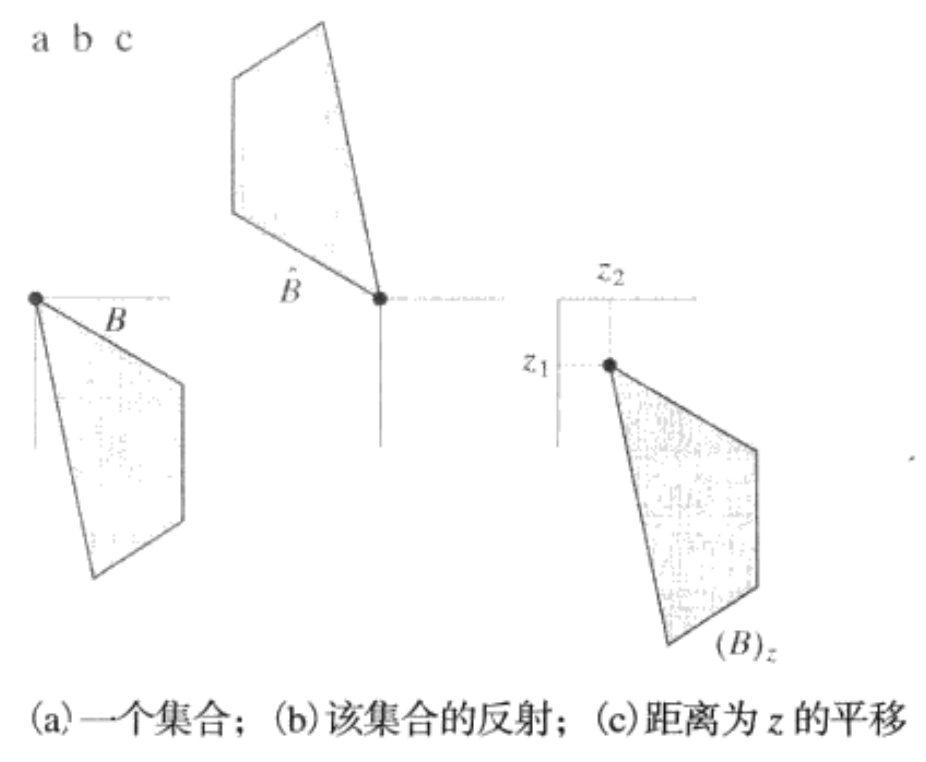
集合 A A A 的补集是不包含于集合 A A A 的所有 元素组成的集合:
A c = { w ∣ w ∉ A } A^{c}\:=\:\left\{w\mid w\notin A\right\} Ac={w∣w∈/A}
集合 A A A 和 B B B 的差,表示为 A − B A-B A−B ,定义为:
A − B = { w ∣ w ∈ A , w ∉ B } = A ∩ B c A-B=\{w\mid w\in A,w\notin B\}=A\cap B^{c} A−B={w∣w∈A,w∈/B}=A∩Bc
作为 Z 2 Z^{2} Z2中的集合 A A A 和 B B B,表示为 A ⊖ B A{\ominus}B A⊖B 的 B B B 对 A A A 的腐蚀为
A ⊖ B = { z ∣ ( B ) z ⊆ A } = { z ∣ ( B ) z ∩ A c = ∅ } A{\ominus}B=\left\{z\mid\left(B\right)_{z}\subseteq A\right\}=\left\{z\mid(B)_{z}\cap A^{c}=\emptyset\right\} A⊖B={z∣(B)z⊆A}={z∣(B)z∩Ac=∅}
表面上,该式指出 B B B 对 A A A 的腐蚀是一个用 z z z 平移的 B B B 包含在 A A A 中的所有的点 z z z 的集合。
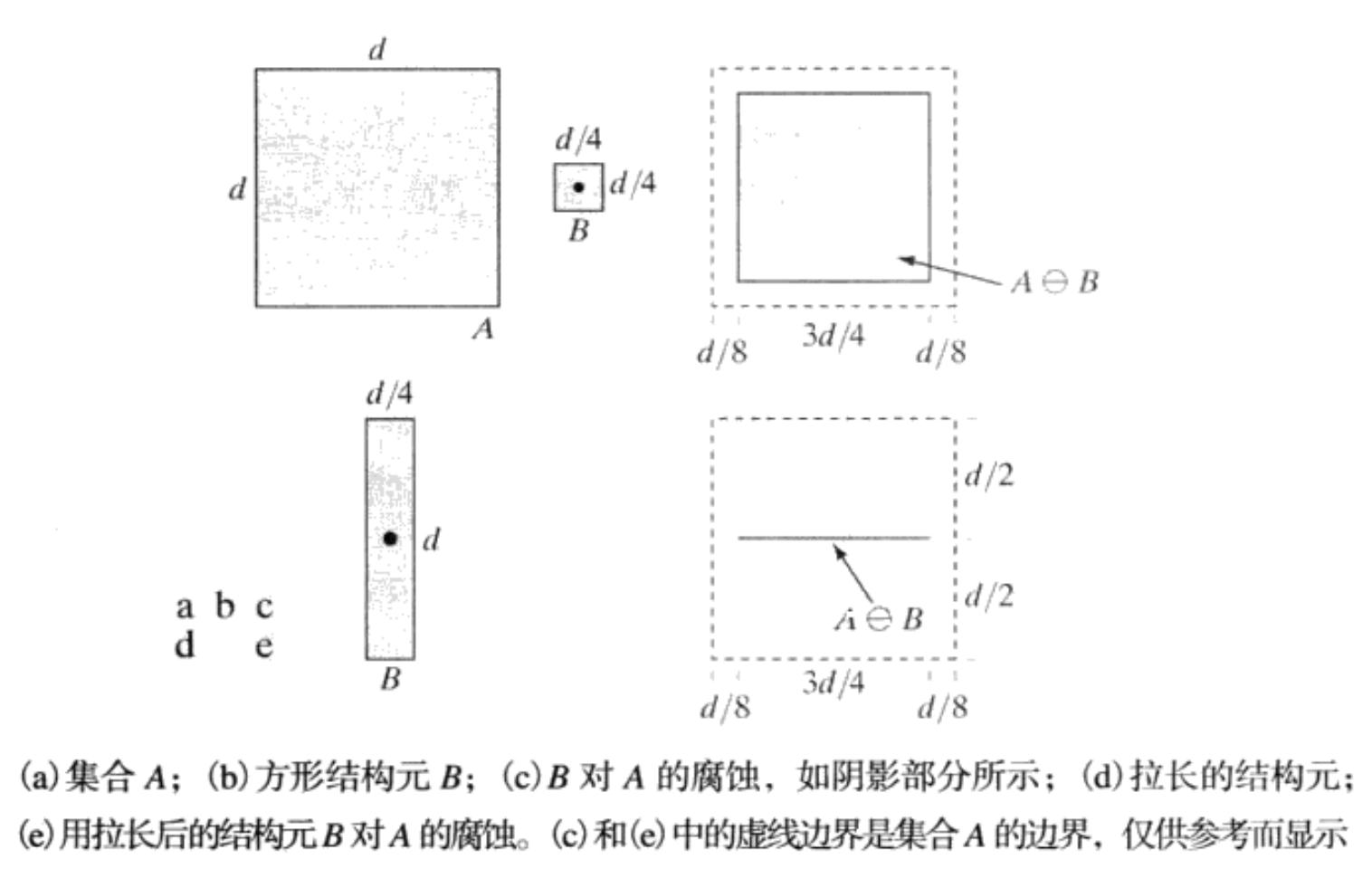
A A A和 B B B 是 Z 2 Z^2 Z2中的集合,表示为 A ⊕ B A\oplus B A⊕B 的 B B B 对 A A A 的膨胀定义为
A ⊕ B = { z ∣ ( B ^ ) z ∩ A ≠ ∅ } = { z ∣ [ ( B ^ ) z ∩ A ] ⊆ A } A\oplus B=\left\{z\mid(\hat{B})_{z}\cap A\neq\emptyset\right\}=\left\{z\mid[(\hat{B})_{z}\cap A]\subseteq A\right\} A⊕B={z∣(B^)z∩A=∅}={z∣[(B^)z∩A]⊆A}
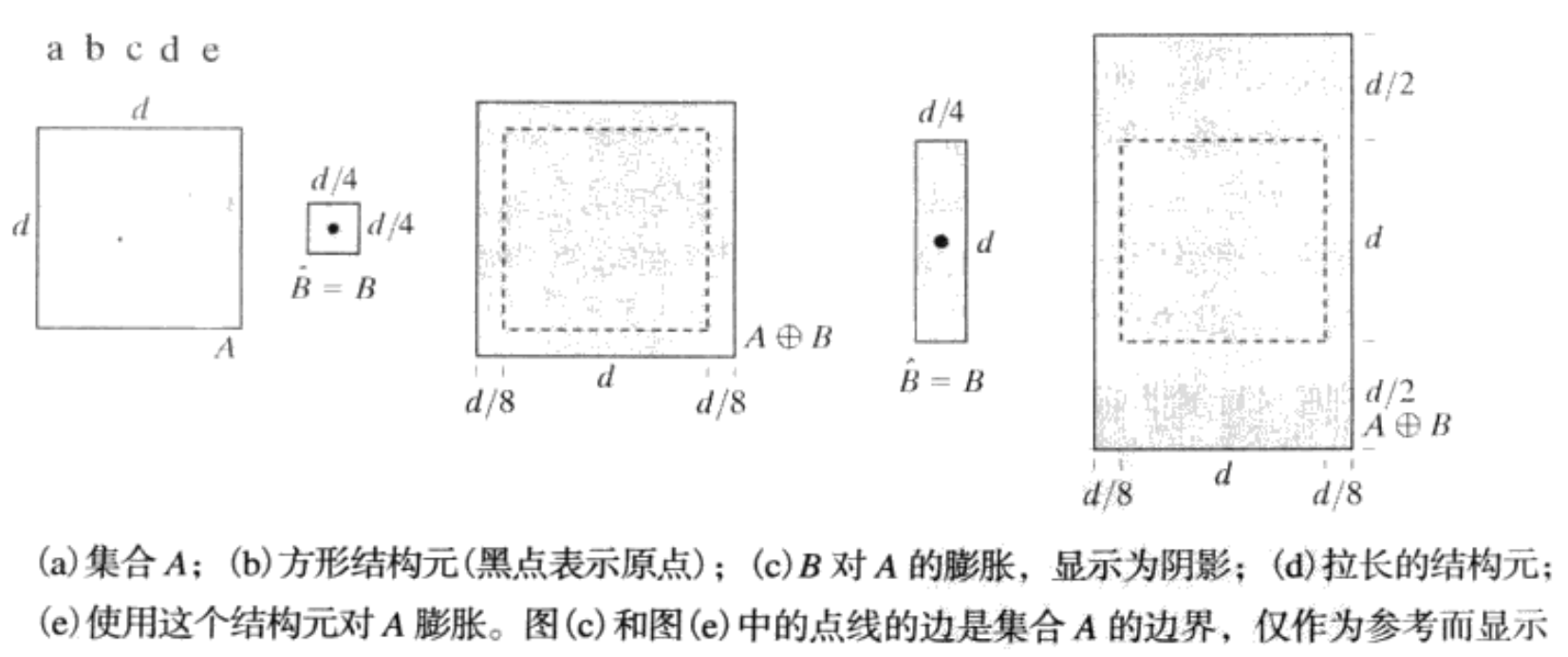
结构元 B B B 对集合 A 的开操作,表示为 A ∘ B A\circ B A∘B , 其定义如下:
A ∘ B = ( A ⊖ B ) ⊕ B A\circ B=(A\ominus B)\oplus B A∘B=(A⊖B)⊕B
因此, B B B 对 A A A 的开操作就是 B B B 对 A A A 的腐蚀,紧接着用 B B B 对结果进行膨胀。
类似地,用结构元 B B B 对集合 A A A 的闭操作,表示为 A•B , 定义如下:
A ∙ B = ( A ⊕ B ) ⊖ B A{\bullet}B=(A\oplus B){\ominus}B A∙B=(A⊕B)⊖B
上式说明, B B B 对集合 A A A 的闭操作就是简单地用 B B B 对 A A A 膨胀,紧接着用 B B B 对结果进行腐蚀。
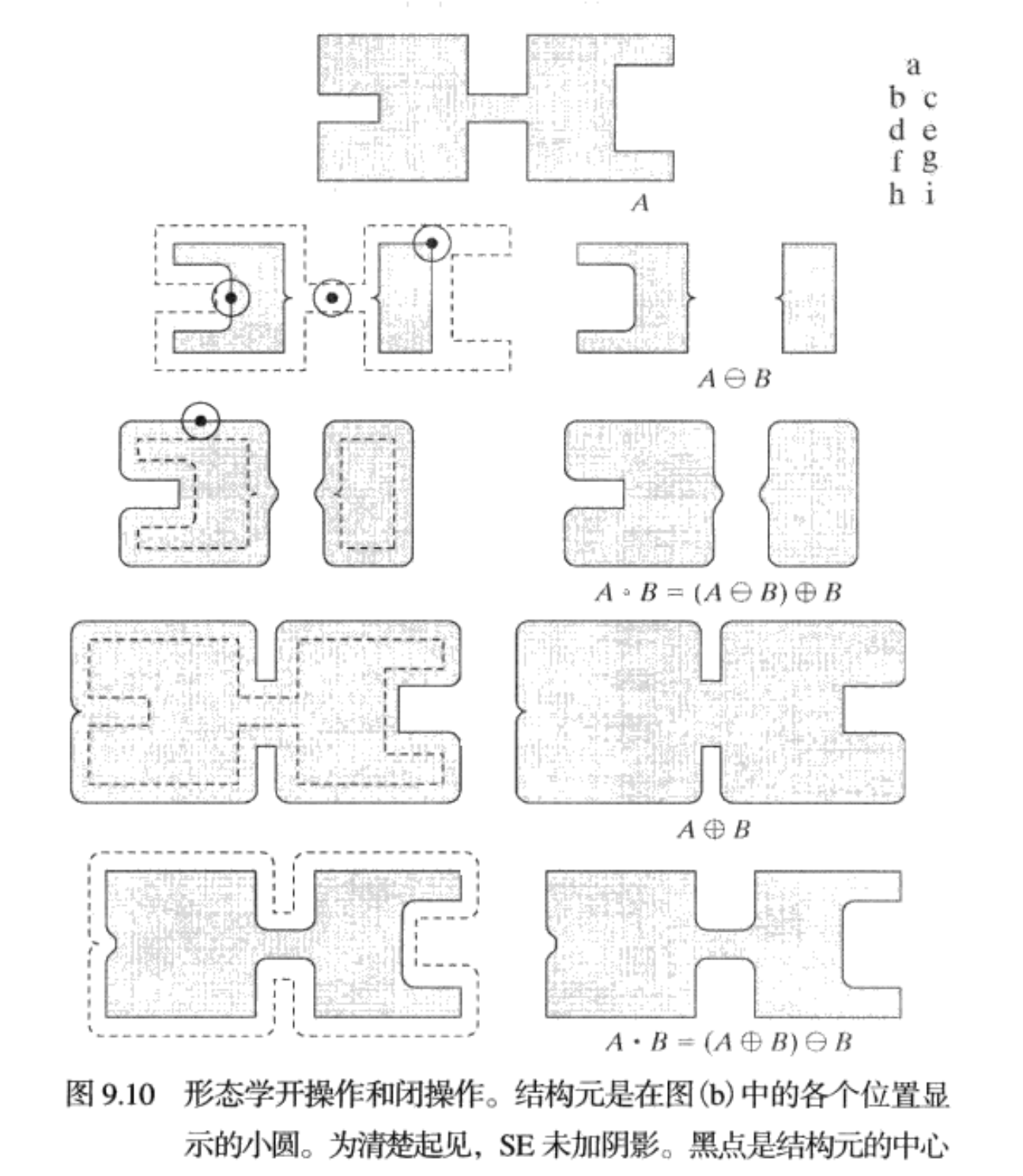
由此可以得到关于开运算的几点结论:
- 开运算能够除去孤立的小点,毛刺和小桥,而总的位置和形状不便。
- 开运算是一个基于几何运算的滤波器。
- 结构元素大小的不同将导致滤波效果的不同。
- 不同的结构元素的选择导致了不同的分割,即提取出不同的特征。
同理也可以得到关于闭运算的几点结论:
- 闭运算能够填平小湖(即小孔),弥合小裂缝,而总的位置和形状不变。
- 闭运算是通过填充图像的凹角来滤波图像的。
- 结构元素大小的不同将导致滤波效果的不同。
- 不同结构元素的选择导致了不同的分割。


![[⑤Meson]: Build Options构建选项](https://img-blog.csdnimg.cn/direct/82fe8507c76b48d386837bb275699740.png)