八大算法排序@希尔排序(C语言版本)-编程知识

希尔排序

概念

希尔排序（Shell Sort）是一种基于直接插入排序的排序算法，又称缩小增量法。其主要思想是通过对数据集合进行多次的直接插入排序，每次使用不同的增量进行直接插入排序，最终使数据基本有序，最后进行一次直接插入排序，达成排序的效果。

算法思想

希尔排序是对直接插入排序的优化算法

示例

让我们回忆一下直接插入排序的特点，下面有两个数组，
数组arr1：
数组1

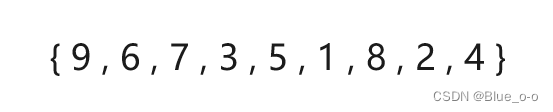
数组arr2：
数组2

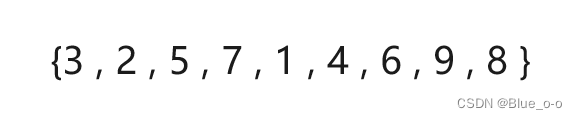
现在使用直接插入排序，分别对数组 arr1 和 arr2 进行升序的排序，达到以下的效果：
排序结果

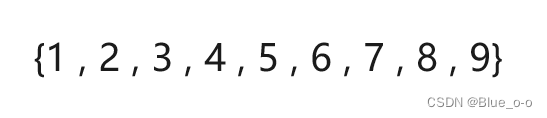
分析

对于数组arr1而言，插入的第一个元素，是数组中最大的元素9。那么对于后续要插入的元素，都要进行的一个步骤是与元素9进行交换。根据最终完成的排序结果，元素9是要排到最后的，即元素9要移动八次才能到达最终的位置。
对于数组arr2而言，插入的第一个元素是3，根据排序完成的最终结果，我们发现只需要对元素3移动两次，就能到达最终的位置。到了最终的位置后，该元素便扎根不移动了。

结论

根据两个数组中的第一个元素插入，在整个排序中的情况。我们能够发现：
要实现升序的排序时，对于直接插入排序而言，“ 数组中较大的元素如果较靠前 ” 的情况，比起 “ 数组中较小的元素较靠前 ” 的情况移动的次数更多，即复杂度更高。这也吻合直接插入排序的特点，如果原数组大体的趋势上越接近我们要实现的排序的效果，那么直接插入排序的效率/时间复杂度相对较低（ 极端情况下，数组已经有序，那么时间复杂度为O(N) ）；如果原数组大体的趋势上与我们要实现的排序的效果相背而驰，那么直接插入排序的效率/时间复杂度相对更高（ 极端情况下，数组是逆序，那么时间复杂度为O(N^2) ）。因此直接插入排序的时间复杂度为O(N^2）。

了解至此，让我们再次解读 “ 希尔排序是对直接插入排序的优化算法 ” 这句话的意思。希尔排序，就是进行多次的直接插入排序，每次使用不同的增量，达到让数组大体上逐渐的趋近有序且是要实现的排序的效果。最后一次使用直接插入排序的算法时，此时因为数组大体上已经趋近于最终的排序效果，所以对于整个数组的元素的移动并不多，因此效率上更高。整体上相对于直接插入排序的效率而言，得到了提高。

算法步骤

在阐述算法步骤前，让我们想这么一个问题：希尔排序是一种多次排序的算法，且每一次的排序都是直接插入排序。那么每一次排序的区别是什么？
带着这个问题，我们对上述的数组arr1进行图文模拟希尔排序的过程。

第一次直接插入排序，选择间距 (下标 ) 等于5的两两元素进行排序。如下图：
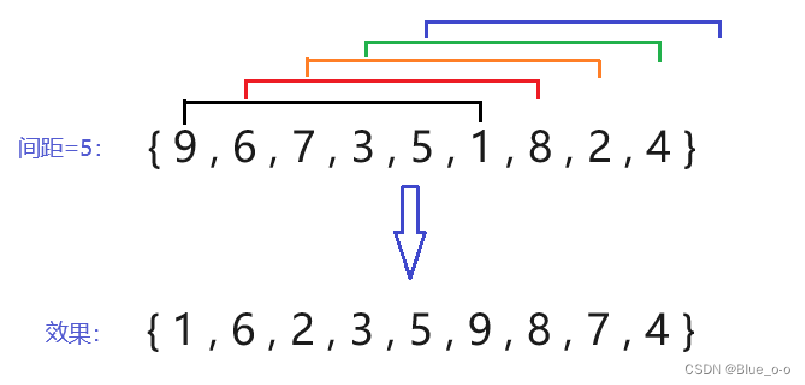
在这里插入图片描述
元素9和元素1，下标间距为5，而距离元素1间距为5的已经超出数据的范围。其他的元素同理，即数组中每个元素有且只有一个与自己距离为5的元素（除了元素5之外）。因此间距为5时，具体的直接插入排序，实现的是：
元素9和元素1的升序排序，元素9和元素1位置互换、
元素6和元素8的升序排序，元素6和元素8位置不变、
元素7和元素2的升序排序，元素7和元素2位置互选、
元素3和元素4的升序排序，元素3和元素4位置不变、
元素5单独一个，则不移动，在原位置上。

也可以这么理解：元素之间间距相等（等于5）且是“ 邻居 ”关系的，划分为一个数组。在原先各自的位置上，对数组的元素进行排序。实现在这些位置上的数组元素是升序/降序的效果。

第二次直接插入排序，选择间距 (下标 ) 等于4的两两元素进行排序。如下图：

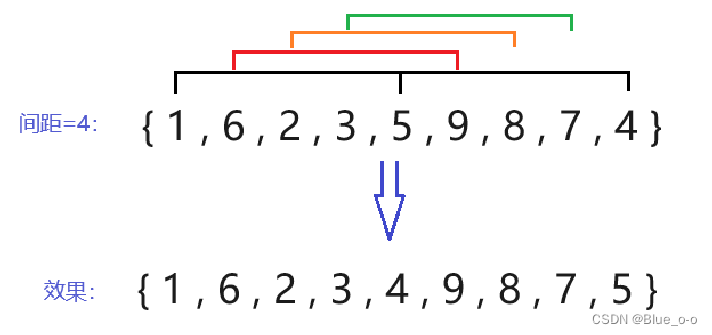
在这里插入图片描述

元素1、5 和元素5、4，两两元素之间间距为4，元素1、5、4组成一个小数组，元素5是元素1的“邻居”，元素4是元素5的 “邻居”，对这个小数组进行升序/降序的排序。如升序排序时，原先的顺序1、5、4，将变为1、4、5。但是位置依旧是原先的那三个位置，只是在这三个位置上的元素达成了升序的排布效果。
而元素6间距为4的只有元素9的位置符合，而距离元素9间距为4的已经超出数组的范围。因此对于元素6切分的小数组中，只有元素6和元素9这两个数据，其他同理。分别对各个切分出来的小数组进行排序，最终达到整体上趋近于想要的排序效果，如升序时，大的元素靠后。
注意：实际排序时，要想想直接插入排序是如何实现的。

同样的思路，我们对间距分别为3、2、1的进行演变模拟：

第三次直接插入排序，选择间距 (下标 ) 等于3的两两元素进行排序。如下图：

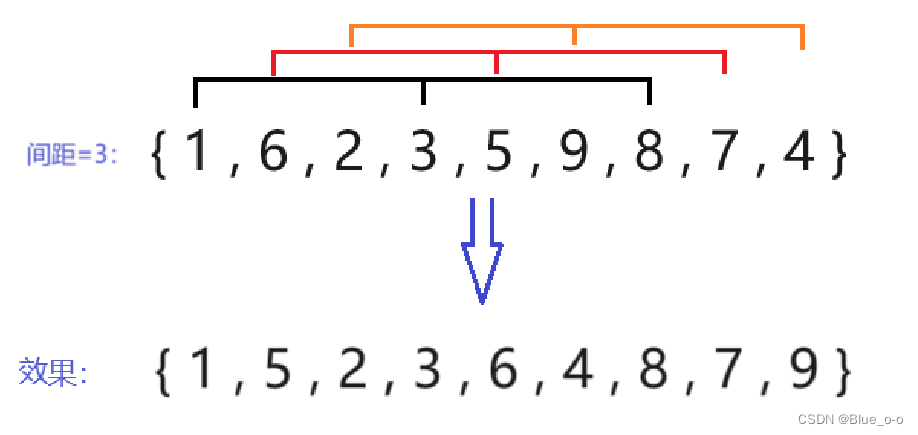
在这里插入图片描述

第四次直接插入排序，选择间距 (下标 ) 等于2的两两元素进行排序。如下图：

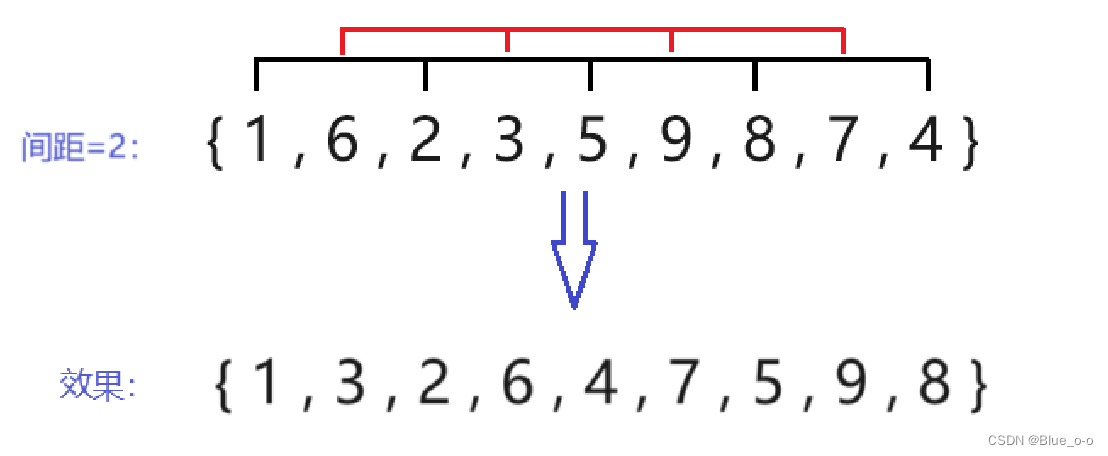
在这里插入图片描述

最后一次直接插入排序，选择间距 (下标 ) 等于1的两两元素进行排序。如下图：
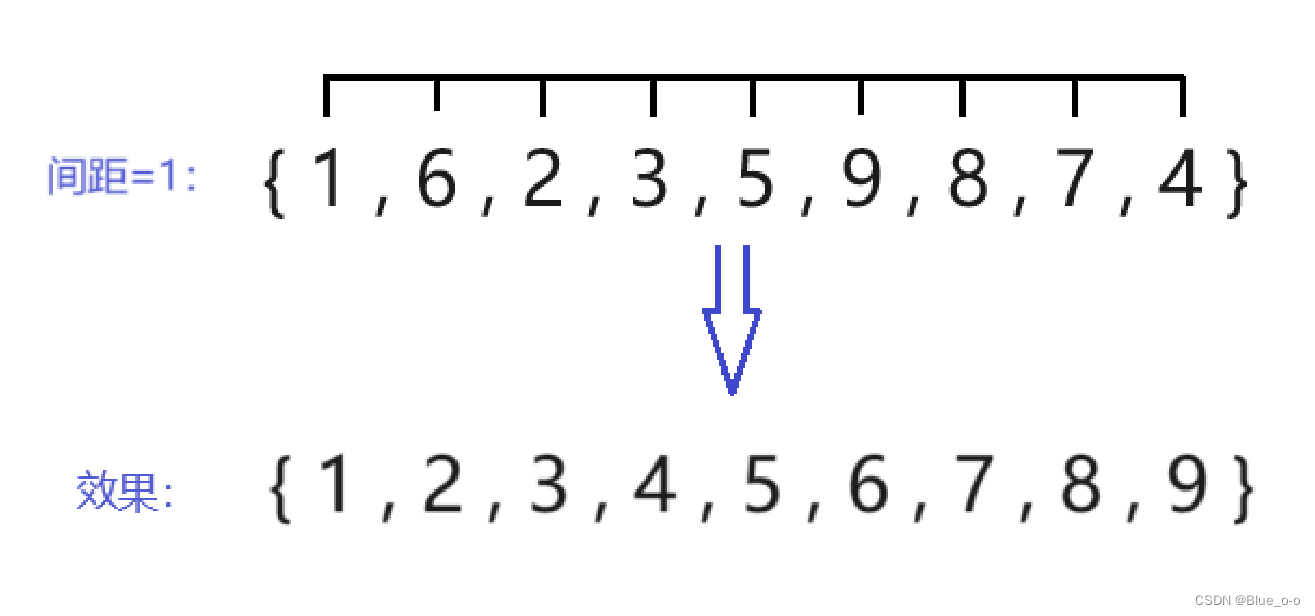
在这里插入图片描述

以上，通过不同的间距，进行总共5次的直接插入排序，最终达成了数组arr1升序的排序效果，整个过程的实现便是希尔排序的算法逻辑了。其中所谓的间距就是前文提到的增量。
我们发现随着不同的增量，执行直接插入排序后，数组在整体上逐渐的形成了升序的效果（较大的数靠后，较小的数靠前）。当增量等于1的时候，排序的想法和直接插入排序的想法一致。

结合以上的学习，下面给出希尔排序的步骤总结：

选择增量序列

选择一个增量序列，这个序列的选择对排序的效率有影响。常用的增量序列有希尔建议的序列（例如，n/2、n/4、n/8…直到增量为1）。

（

注释：
n为数组的个数，如上述对n=9的数组arr1模拟中。选择的增量序列为5、4、3、2、1。细心的同学在观察上述模拟过程图中可以发现，有些间距的直接插入排序，对数组的变动并不大。比如间距为4的时候，只是对元素5和元素4进行了交换，其他的并没有变动。对于这种间距的直接插入排序，效果不大，但是却是实打实造成一定效率的消耗的，我们可以排除掉。
结论：不同的增量序列，对排序的效率是有影响的。如何选取一个高效的增量序列，这牵扯到数学问题。根据前人的计算，选择“ n/2、n/4、n/8…1 ”序列或者“ n/3、n/9、…1 ”序列时，效率最理想。
注：要确保增量为1的直接插入排序存在。
）

按增量分组

将待排序的元素按照增量分成若干个子序列，对每个子序列进行插入排序。这样，每个子序列都是部分有序的。

（

注释：
如上述间距为2时，将数组 arr1 切分为两个子序列，分别是 { 1 , 2 , 5 , 8 ,4 } 、{ 6 , 3 , 9 , 7 }。然后分别对这两个子序列进行插入排序，最终在数组 arr1 中，达成了各个子序列所在的位置是有序的。arr1 数组整体上也趋近于有序。
）

逐步缩小增量

重复上述步骤，逐步减小增量，直至增量为1。当增量为1时，整个序列基本有序，再进行一次直接插入排序，排序完成。

（

注释：
如上述间距从5、4、3、2逐步减小时，数组 arr1 整体上已经愈发的有序。当间距/增量减小为1时，整个数组基本是有序的状态，这是进行直接插入排序，完成最终的排序效果的同时也大大的增大了排序的效率。
）

算法优势

希尔排序的优势在于，它可以在开始时快速地将较小的元素移动到合适的位置，从而减小后续插入排序的工作量。这样，希尔排序相较于直接插入排序在效率上有所提高，特别是对于较大数据集合。虽然希尔排序不如一些更现代的排序算法，如快速排序或归并排序，但在某些特定场景下仍然有其优势。

简洁而言，希尔排序就是对数组进行切分，隔开间距的排序、让数组整体上接近有序。再每次缩短间距，一次次的下来，数组整体上已经临近与有序的状态。当间距等于1时，排序的想法和直接插入排序的想法一致。
下面是代码的实现。

代码实现

核心算法

// 交换数值函数
void swap(int* x1,int* x2)
{int tmp=*x1;*x1=*x2;*x2=tmp;
}// 直接插入排序
void InsertSort(int* a, int n)
{assert(a);// 最后一个 n-1(下标) 插入到 前n-2个排好序列的数 // i是有序序列的下标，当i=n-1，即数组最后一个数的下标时，则整个数组就是有序的序列了for (int i = 0; i < n - 1; i++){// 单趟排序，设定end为已排序部分的最后一个元素下标int end = i;	// 有序序列的最后一个下标是iint tmp = a[end + 1];  // a[end+1] 是即将要插入的数据while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;	}// 出了for循环，利用直接插入算法实现对数组的升序/降序的效果
}

希尔排序代码实现：

// 交换数值函数
void swap(int* x1,int* x2)
{int tmp=*x1;*x1=*x2;*x2=tmp;
}// 希尔排序 : 时间复杂度O(N^1.3 - N^2)
void ShellSort(int* a, int n)
{// 1、gap>1相当于预算排序，让数组接近有序// 2、gap == 1就相当于直接插入排序，保证有序int gap = n;while (gap > 1){gap = gap / 3 + 1;//增量gap，+1保证了最后一次gap一定是1//gap == 1 最后一次就相当于直接插入排序// 直接插入排序for (int i = 0; i < n - gap; i++){int end = i;	// 有序数组的最后一个元素的下标int tmp = a[end + gap];	// 要插入的数据，与要排序的间距为gapwhile (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}

观察以上代码，与直接插入排序的代码实现比对发现，希尔排序在直接插入排序外面多了一层循环，用来确保每次的直接插入排序的增量不同。而希尔排序循环内的直接插入排序与直接插入排序的区别就在于元素之间、边界的差异。具体的可以根据代码自己在图纸上结合上述演示的演示图带入数据过一遍。

时间复杂度

希尔排序的时间复杂度介于N^1.3 - N^2 之间，即O(N^1.3 - N^2)。具体的计算过程就不加以解释了，有兴趣的可以自行在网上了解、

空间复杂度

O（1）。

特性总结

1、希尔排序是对直接插入排序的优化；
2.、当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的
了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的
对比；
3.、希尔排序的时间复杂度不好计算，需要进行推导，推导出来平均时间复杂度： O(N^1.3—
N^2）；
4.、稳定性：不稳定。