《数字图像处理-OpenCV/Python》连载：空间滤波之高斯滤波器-编程知识

《数字图像处理-OpenCV/Python》连载：空间滤波之高斯滤波器

本书京东优惠购书链接 https://item.jd.com/14098452.html
本书CSDN 独家连载专栏 https://blog.csdn.net/youcans/category_12418787.html

在这里插入图片描述

第 10 章图像卷积与空间滤波

图像滤波是指在尽可能保留图像细节特征的条件下对目标图像的噪声进行抑制，是常用的图像处理方法。
空间滤波也称空间域滤波，滤波器规定了邻域形状与邻域像素的处理方法。线性滤波通过图像与滤波器核进行卷积计算，非线性滤波则包含了绝对值、置零和统计等非线性运算，通过逻辑运算实现图像滤波。

本章内容概要

学习图像的卷积运算，介绍可分离卷积核与图像的边界扩充。
学习典型的空间滤波器，包括盒式滤波器和高斯滤波器。
介绍常用的非线性滤波器，包括统计排序滤波器、自适应滤波器和双边滤波器。
学习常用的梯度算子，包括Laplacian算子、Sobel算子和Scharr算子。
介绍图像金字塔，包括高斯金字塔和拉普拉斯金字塔。

10.3　空间滤波之高斯滤波器

高斯滤波器（Gaussian Filter）是以高斯核函数为权函数的滤波器，在信号和图像处理领域的应用非常广泛。

高斯核函数的数学描述如下。

$=\frac{1}{2\pi\sigma^2} e^{-r^2/2\sigma^2}$

式中， $\sigma$ 是高斯核的标准差（尺度因子）；r 表示任意点到中心点的距离。

高斯卷积核有很多重要的性质。
（1）高斯卷积核是圆对称（各向同性）的，中心点的权重最大，离中心点越远，权重越小。
（2）高斯卷积核是可分离卷积核，可以通过水平卷积核和垂直卷积核实现对图像的卷积。
（3）高斯卷积核的有效尺寸为 $（6\sigma+1) （6\sigma+1)$ ，尺寸越大，平滑程度越高。

OpenCV中的函数cv.GaussianBlur用于实现高斯低通滤波，函数cv.getGaussianKernel用于计算一维高斯滤波器的系数。

函数原型

cv.GaussianBlur(src, ksize, sigmaX[, dst, sigmaY, borderType]) → dst
cv.getGaussianKernel(ksize, sigma[, ktype]) → retval

参数说明

src：输入图像，是多维Numpy数组，允许为单通道图像或多通道图像。
dst：输出图像，大小和通道数与src相同。
ksize：高斯滤波器核的尺寸，格式为元组(w,h)，0表示由sigma计算。
sigmaX：x轴方向的高斯核标准差。
sigmaY：y轴方向的高斯核标准差，可选项，默认值为0。
sigma：高斯核的标准差，是浮点型数据。
borderType：边界扩充类型，可选项，不支持BORDER_WRAP。
ktype：高斯核的数据类型，可选项，默认值为CV_64F，可选CV_32F。
retval：返回值，是一维高斯核的系数，形状为(ksize,1)的Numpy数组。

注意问题

（1）高斯核标准差sigmaX不能省略，sigmaY可以省略，缺省时，表示sigmaY=sigmaX。
（2）如果sigmaX=sigmaY=0，则由ksize计算：sigma=0.3*[(ksize-1)/2-1]+0.8 。
（3）如果 ksize=0，则由 sigma 自动计算 ksize。
（4） ksize 的宽度 w 与高度 h 必须是奇数。
（5）注意在函数cv.GaussianBlur中，ksize的格式为元组 (w,h)，表示滤波器的尺寸；而在函数cv.getGaussianKernel中，ksize的格式为数值，表示滤波器的孔径。
（6）使用函数 cv.GaussianBlur时，推荐对ksize、sigmaX、sigmaY都进行赋值。
（7）函数cv.getGaussianKernel能返回一维高斯滤波器的系数，形状为(ksize,1)。

【例程1003】空间滤波之高斯滤波器

本例程介绍高斯滤波器的使用。

# 【1003】空间滤波之高斯低通滤波器
import cv2 as cv
import numpy as np
from matplotlib import pyplot as pltif __name__ == '__main__':img = cv.imread("../images/Fig1001.png", flags=0)  # 读取灰度图像# (1) 计算高斯核kernX = cv.getGaussianKernel(5, 0)  # 一维高斯核kernel = kernX * kernX.T  # 二维高斯核print("1D kernel of Gaussian:{}".format(kernX.shape))print(kernX.T.round(4))print("2D kernel of Gaussian:{}".format(kernel.shape))print(kernel.round(4))# (2) 高斯低通滤波核ksize = (11, 11)  # 高斯滤波器核的尺寸GaussBlur11 = cv.GaussianBlur(img, ksize, 0)  # sigma 由 ksize 计算ksize = (43, 43)GaussBlur43 = cv.GaussianBlur(img, ksize, 0)plt.figure(figsize=(9, 3.2))plt.subplot(131), plt.axis('off'), plt.title("1. Original")plt.imshow(img, cmap='gray', vmin=0, vmax=255)plt.subplot(132), plt.axis('off'), plt.title("2. GaussianFilter (k=11)")plt.imshow(GaussBlur11, cmap='gray', vmin=0, vmax=255)plt.subplot(133), plt.axis('off'), plt.title("3. GaussianFilter (k=43)")plt.imshow(GaussBlur43, cmap='gray', vmin=0, vmax=255)plt.tight_layout()plt.show()

运行结果：

1D kernel of Gaussian:(5, 1)[[0.0625 0.25   0.375  0.25   0.0625]]
2D kernel of Gaussian:(5, 5)[[0.0039 0.0156 0.0234 0.0156 0.0039][0.0156 0.0625 0.0938 0.0625 0.0156][0.0234 0.0938 0.1406 0.0938 0.0234][0.0156 0.0625 0.0938 0.0625 0.0156][0.0039 0.0156 0.0234 0.0156 0.0039]]

程序说明：

（1）函数cv.getGaussianKernel能返回一维高斯滤波器的系数，可以由此计算并得到二维高斯滤波器的系数。
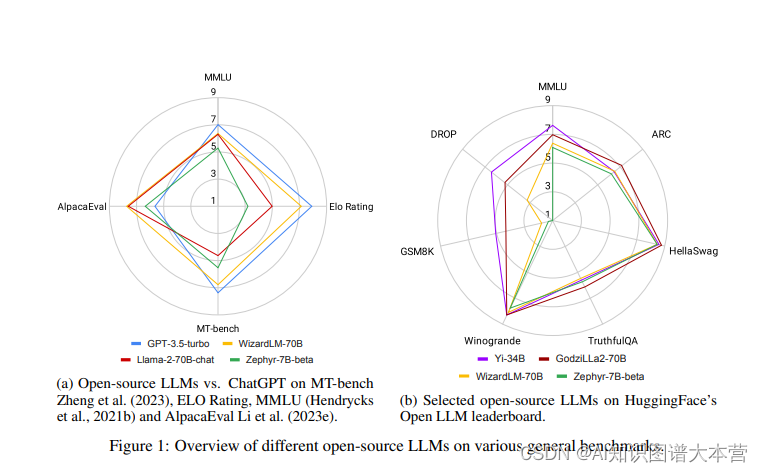
（2）运行结果，高斯低通滤波器的滤波图像如图10-3所示。图10-3(2)和图10-3(3)所示为使用不同滤波器尺寸的平滑图像。高斯核的标准差sigma越大，高斯滤波器核的尺寸ksize越大，滤波图像越模糊。

在这里插入图片描述