4.1 判别分析的目标

主要目的：判别一个个体所属类别

4.2 距离判别

都选用用马氏距离

4.2.1 判别准则

化简的证明：

称为判别函数，为判别系数。

4.2.2 误判概率

【1】当两个正态总体的协方差相同

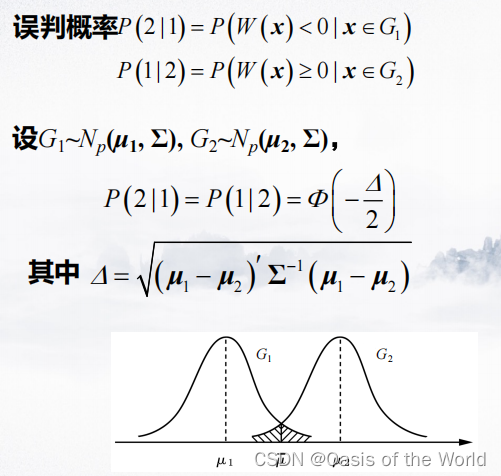
证明：

当两个正态总体重合的时候误判概率是1/2

所以只有当两个总体的均值相差较大时，进行判别分析才有意义

4.2.3 怎样定义均值相差较大呢????(假设检验)

（1）理论知识

（2）假设检验例子

4.2.4 例题1：当协方差和均值已知

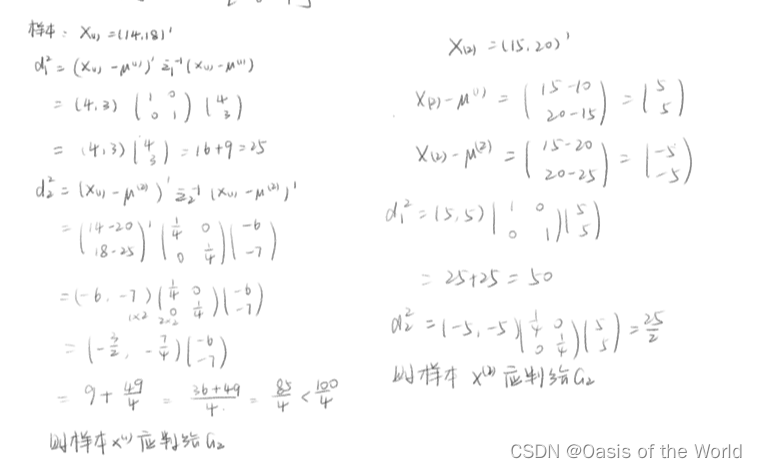
4.2.5 例题2：当协方差和方差未知

4.2.6 python代码实现

#coding=utf-8
import numpy
x = numpy.array([[3,4],[5,6],[2,2],[8,4]])
print("x矩阵的维度：",x.ndim)  # 二维向量组成的矩阵
xT = x.T
D = numpy.cov(xT)
invD = numpy.linalg.inv(D)
tp = x[0] - x[1]
print(numpy.sqrt(numpy.dot(numpy.dot(tp, invD), tp.T)))

4.3 贝叶斯判别

4.3.1 贝叶斯最大后验概率判别的例子

4.3.2 误判代价最小化的贝叶斯判别

（1）理论

【1】有两个类时

证明：

【有多个类时】

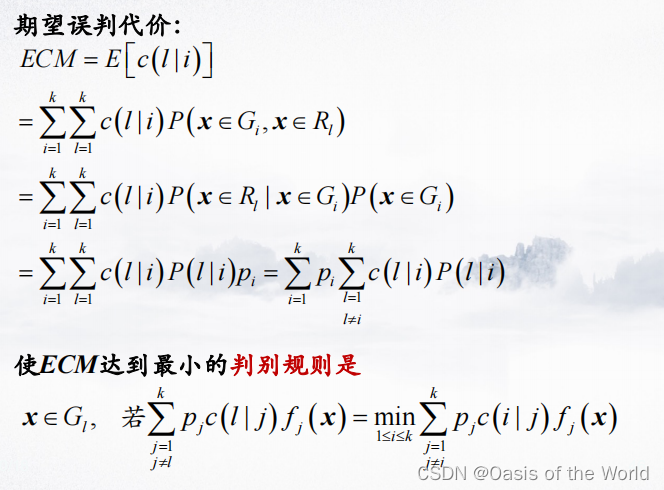
建议第二类的时候也用这个判断这样就会错了！

（2）例题

【只有两个类的时候】

先计算 最小ECM判别规则： 

【有三个类】

4.4 Fisher判别

（1）理论

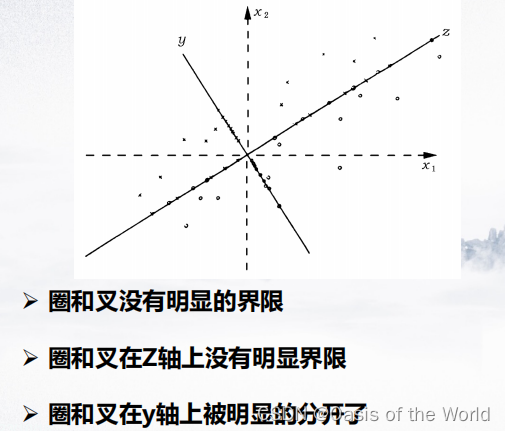
给一个向量，样本值全投影在这个向量上！注意Fisher判别的数据是有标签的，但是主成分分析的数据是没有标签的！

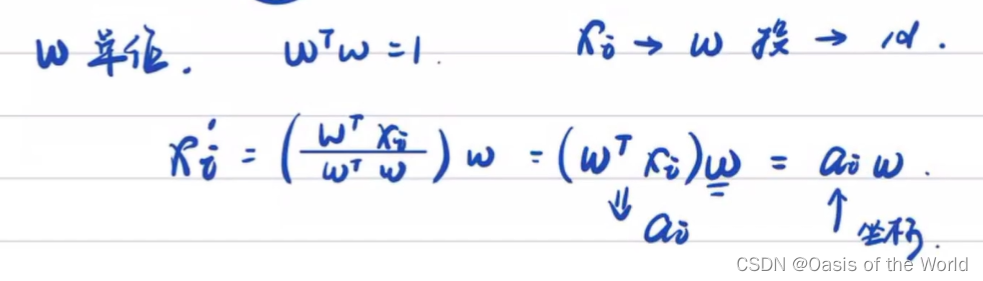
则可以把x这个集合映射到a这个几何上

1、对每个类算均值

对于二分类问题：

而Fisher判别式要找一个最好的w，使投影后的点分的比较开

完全的分开：类与类均值相差大，且同类之间的散度（利用方差的概念定义散度）比较低

这变成一个多目标优化问题，多目标优化一般考虑变成单目标优化！

在Fisher中，利用一元方差检验：

则这个问题就变成 最大化：

求解最大值，其中参数使。则对求导：

总体计算思路：

特征值就是最后的解？？？？

最后的解： 是最大的特征根，而解（向量）是特征值对应的单位特征向量！！！

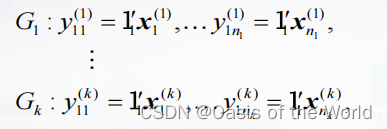
当有两个判别函数的时候，会产生两个y值就相当于把原来的点投影到二维的平面上！

当有一个判别函数的时候，就相当于把原来的点投影到一条直线上！

投影后得到二维数据之后，用距离判别或者贝叶斯判别的方法将新样本进行分类即可！！

具体选用多少判别函数呢？

主要根据贡献率：

Fisher判别的思想是：投影（旋转坐标系？或者降维？），将k组p维数据投影到某个地方，使组与组之间的投影尽可能分开。

衡量之间组与组之间的分离程度：fisher采用了一元方差分析（F检验！！！）的思想。

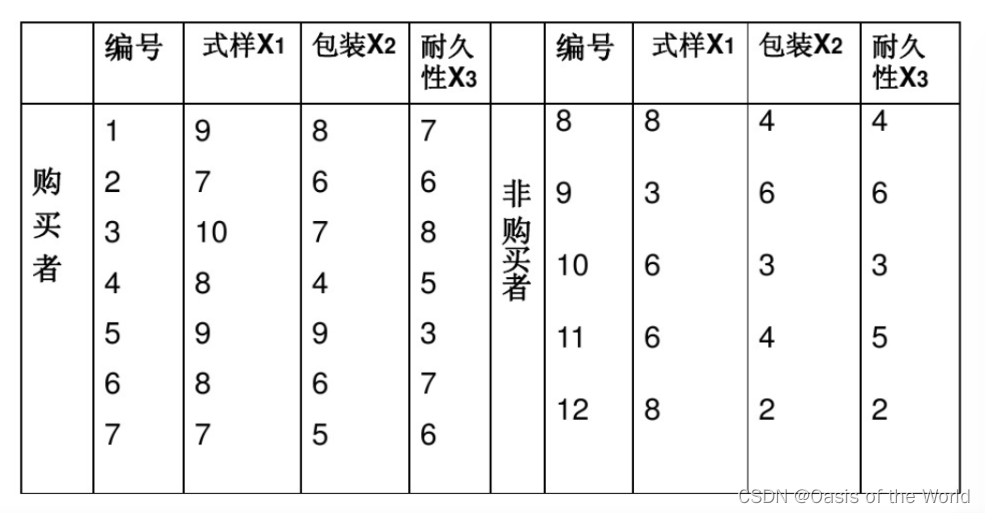
（2）例题