目录
- 堆排序
- 大堆排序
- 概念
- 算法思想
- 建堆
- 建堆核心算法
- 建堆的代码
- 排序代码实现
- 小堆排序
- 代码实现
- 时间复杂度
- 空间复杂度
堆排序
堆排序借用的是堆的特性来实现排序功能的。大堆需要满足父节点大于子节点,因此堆顶是整个数组中的最大元素。小堆则相反,要求父节点小于子节点,因此父节点是整个数组中最小元素。
借助这一特性,对于大堆,我们可以将堆顶的元素,和堆的最后一个元素置换,这样便将最大的数排到了最后面。同时将堆顶的有效个数减1。但是置换上来堆顶的元素,也就破坏了堆的结构,但是堆顶元素的左右子节点依旧是堆的结构,因此可以对堆顶进行调整,然其继续满足堆的特性。这样便找出第二大的元素,继续重复上述动作,便能将大的数组都往后挪动。待到只剩下一个有效数据时,便拍好了数组。大家认为这是一个升序的数组呢?还是一个降序的数组呢?
答案显而易见,使用大堆进行排序,结果是升序的效果。同样的思路,使用小堆进行排序,结果是降序的结果。
因此,得出一个结论:
想要对数组进行升序的排序,使用大堆;
想要对数组进行降序的排序,使用小堆;
大堆排序
概念
大堆概念:每个节点(父节点)的值都大于或等于其子节点的值。
大堆排序借用的便是大堆的特性,将堆顶的元素和堆的最后一个元素进行置换,置换上来堆顶的数据再进行堆结构的调整。然后重复以上动作,实现排序功能。
算法思想
要想实现大堆排序,首先需要对数组建立起大堆的结构。下面我们使用数组 arr[] = { 6 , 4 , 3 , 9 , 2 , 1 ,5 ,7 ,8 };来模拟演示大堆的构建,以及排序的大体过程。如下是数组的初始状态:

首先,让我们来看看堆的结构是如何产生的。
建堆
首先,要明确一点的就是:堆是基于完全二叉树而演变出来的一种数据结构。分为最大堆和最小堆两种类型,但它们都是完全二叉树。完全二叉树结构特点如下:
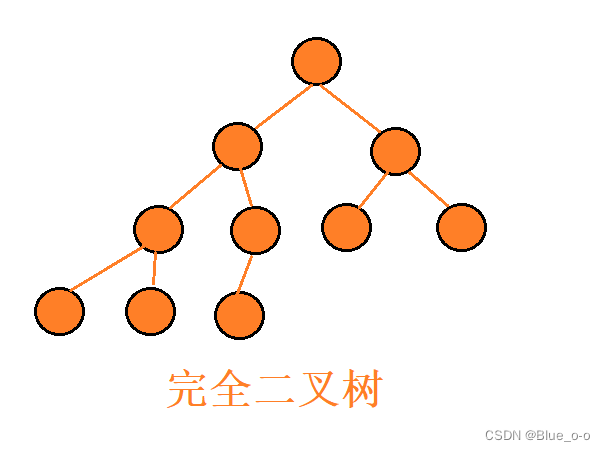
注意:完全二叉树每个节点必须是从左到右依次遍布的,中间不能跳跃,如第四层的第三个节点,必须是第三层第二个节点的左节点,否则将不满足完全二叉树的特点。
了解以上知识后,还得须知建堆的核心算法是 “向下调整算法” 。通过算法的一步步调整,一步步建立起堆这一结构。但是!该算法有个前提,就是调整的节点的左右子节点必须是堆的结构。
有同学可能有疑惑,这不是扯淡吗?我就是要建立的堆结构,又要我满足调整的节点的左右子节点也是堆结构,闹着玩儿呢?
并不是的,正所谓没有条件,便创造出条件。我们可以从下往上进行建堆啊!比如回到原数组 arr[] = { 6 , 4 , 3 , 9 , 2 , 1 ,5 ,7 ,8 };我们先对数组模拟出堆的结构出来:
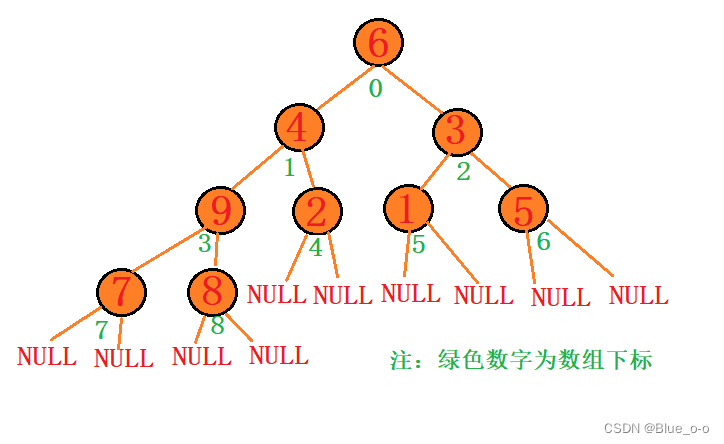
肉眼可见的,原数组模拟出来的完全二叉树,并不符合堆的结构特点。那么如何做到前面所说的,创造出前提条件,进行建堆呢?从堆顶向下进行调整是不可能的,因为堆顶的元素6不满足核心算法的前提条件。但是!我们可以对元素9进行调堆啊,元素9不就正好满足核心算法的前提条件嘛。
首先元素9有左右两个子节点7和8。元素7和元素8左右子节点都为空节点,那么元素7和元素8可以认为是堆的结构,因此元素9左右子节点都是堆结构这一前提条件便满足了。可以使用建堆的核心算法,从元素9开始依次往上建堆。
元素9建成堆结构后,下标减1。开始对元素3进行建堆,同样的元素3也满足核心算法的前提条件,同样可以使用核心算法进行堆结构的建立。接着就是元素4,元素4此时也满足了左右子节点都是堆结构的条件,同样进行堆的调节建立,最终是元素6也就是堆顶的调节,而这时堆顶也满足了左右子节点都是堆结构的前提条件,同样利用 “向下调整算法” 进行堆结构的建立。至此完成整个数组的堆结构构建。
(注:
是如何找到要从哪一个节点进行堆的构建的?利用子节点找父节点的方法!如数组有n个元素,最后一个元素的下标则为n-1,根据完全二叉树的特点,最后一个元素的父节点的下标为:(n-1-1)/ 2。
)
建堆核心算法
// 两数交换
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 向下调整算法
/*
传入参数:
ret:需要建立的数组
root:需要开始调节的节点
n:数组的个数
*/
void AdjustDown(int* ret,int n,int root)
{int parent = root;// 父节点,也就是要调节的节点int child = parent*2+1;// 子节点/孩子,默认是左节点while(child<n){// 找出左右孩子,最大的孩子,同时要考虑只有左孩子的情况if(child+1<n && ret[child+1] > child[child]){child++;// 如果右孩子比左孩子大,则存储右孩子的下标}// 如果 子节点大于父节点,则子节点向上进行调整if(ret[parent] < ret[child]){swap(ret[parent],ret[child]);parent = child;child=parent*2+1;}else // 父节点大于子节点则退出循环(注意父节点左右子节点都是堆的结构){break;}}
}
建堆的代码
// 升序 - 建大堆
void CreateHeap(int* a, int n)
{// 建大堆,从最后一个节点的父节点开始建立for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDowm(a, n, i);}
}
建完堆后的数组如下所示:
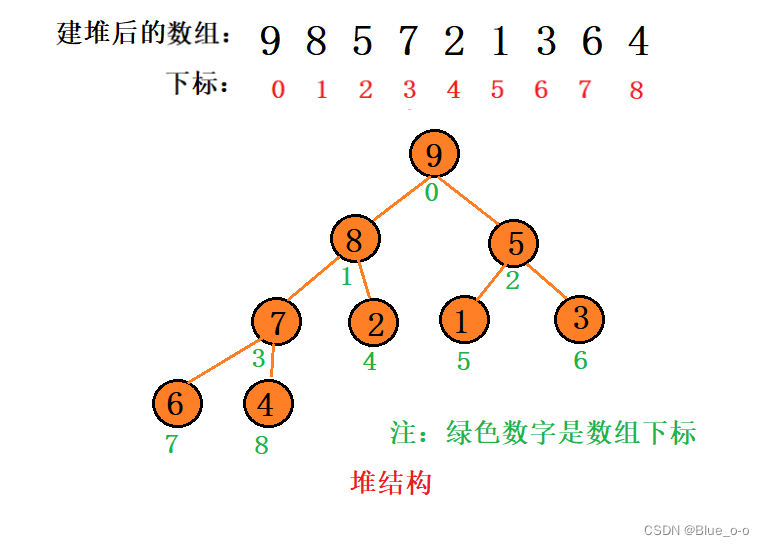
至此,我们实现了对数组建堆这一个数据结构的条件。接下来便能对其进行排序了。
排序代码实现
void SortHeap(int* a,int n)
{// 排序for (int i = 1; i < n; i++){Swap(&a[0], &a[n - i]); // 将堆顶元素与堆的最后一个元素交换AdjustDowm(a, n - i, 0); // 交换上堆顶的元素进行堆的调节,使其依旧保持大堆的结构特性}}
至此,便借用大堆的特性,实现了升序的排序效果。
小堆排序
概念和算法思想和大堆差不多,便不过多冗余介绍了,下面直接给出小堆排序的实现的降序排序代码。
代码实现
// 两数交换
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 向下调整算法 - 前提:左右子树都是堆
void AdjustDowm(int* a, int n, int root)
{int parent = root;int child = parent * 2 + 1;//默认左孩子while (child < n){// 找出左右子节点中,最小的子节点if (child + 1 < n && a[child + 1] < a[child]){child++;}// 如果父节点比子节点大,则将子节点向上调整if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break; // 退出循环}}
}// 降序 - 建小堆
void HeapSort(int* a, int n)
{// 建大堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDowm(a, n, i);}//PrintArr(a,n);//查看建堆后的数组// 排序for (int i = 1; i < n; i++){Swap(&a[0], &a[n - i]);AdjustDowm(a, n - i, 0);}}
与大堆的差别仅改变了核心算法中的两处地方,如下:

下面介绍一下堆排序的时间复杂度和空间复杂度。
时间复杂度
O(N*logN)
大体计算如下:
建堆时间复杂度为O(N);
堆排序的时间复杂度为O(N*logN),因为将堆顶元素置换以后,还需要进行调堆,调堆的时间复杂度为O(logN)。每排一个元素需要进行一次调堆,所以排完整个数组的时间复杂度为O(N*logN)。
所以总的时间复杂度为:O(N+N*logN)。两者记录较大的,所以时间复杂度为O(N*logN)。
空间复杂度
O(1);
堆排序过程中,都是在原数组上进行的,没有申请空间,所以空间复杂度为O(1)。