简述数据结构，抽象数据结构和数据类型之间的异同。

数据结构，抽象数据结构和数据类型本质上来说是同一概念，数据类型是程序设计中实现了的数据结构，而抽象数据结构是数据类型的进一步抽象和发展，借助数据类型可以在程序中完成抽象数据类型。数据类型是程序设计语言中的一个概念，是一个值的集合和运算的集合。抽象数据类型是一个数学模型和定义在该模型上的一组运算。

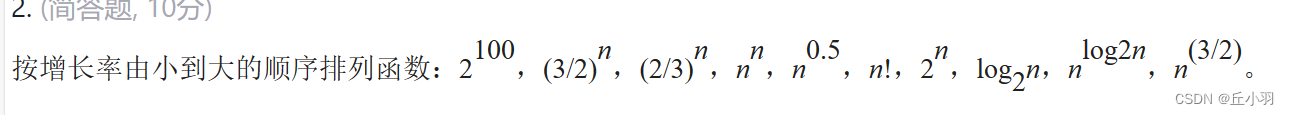
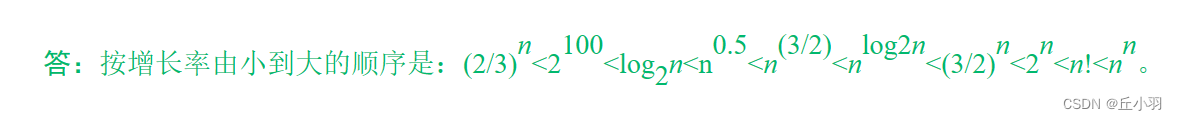
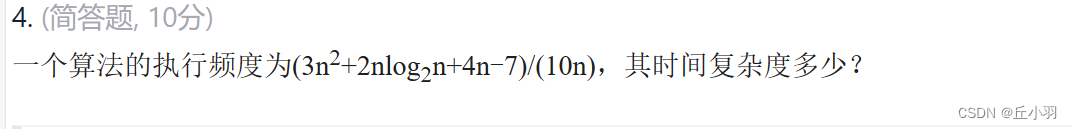
简述逻辑结构和存储结构之间的关系：

在数据结构中，逻辑结构与计算机无关，存储结构是数据元素之间的逻辑关系在计算机中的表示，存储结构不仅将逻辑结构中的所有数据元素存储到计算机内存中，而且还在内存中存储各数据结构间的逻辑关系。通常情况下，一种逻辑结构可以有多种数据结构，例如：线性结构可以采用顺序存储或链式存储。

简述顺序表和链式表存储方式的主要优缺点。

顺序表的优点是可以随机存储元素，存储密度高，结构简单，缺点是需要一片地址连续的存储空间，不便于插入和删除元素（需要移动大量元素 ），表的初始容量难以确定。链表的优点是便于结点的插入和删除（只需要修改指针属性，不需要移动结点），表的容量扩充十分方便，缺点是不能进行随机访存，只能顺序访问，另外在每个结点上增加指针属性，导致存储密度低。

对单链表设置一个头结点的作用是什么？

带头结点时，空表也存在一个头结点，从而统一了空表和非空表的处理。
在单链表中插入和删除结点时，都需要修改前驱结点的指针属性，带头结点时任何数据节点都有前驱结点，这样使得插入和删除操作更加方便。

在单链表，双链表和循环链表中，若只知道指针p指向某个结点，不知道头结点，能否将p删除如果可以，其时间复杂度是多少？

对于单链表来说，不能将p结点删除，只能找到其后继结点，但是其前驱结点未知，头结点未知，前驱结点无法访问，不能删除。
双链表来说能根据已知结点找到其前驱结点和后继结点，所以可以删除。时间复杂度是O（1）。
循环链表可以找到其后继结点，而且可以通过查找得到p的前驱结点。可以删除，时间复杂度是O（n）。

简述线性表，栈和队列的异同。

线性表，栈和队列的相同点就是他们的逻辑关系都是线性关系，不同点是运算不同，线性表可以在两端和中间任何位置插入和删除元素，而栈只能在一端插入和删除元素，队列只能在一端插入元素，在另一端删除元素。

有n个不同的元素经过一个栈能产生的出栈序列个数是多少个？

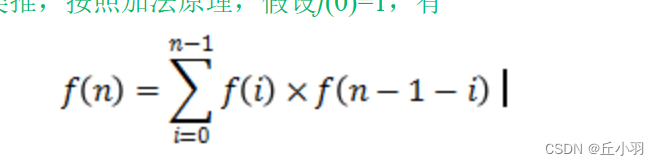
什么叫做队列的假溢出，如何解决假溢出？

在非循环顺序队中，当队尾指针已经到达数组的上界，不能再进行进队操作，但是其实数组中还有空位置，这就叫假溢出，解决假溢出的方式之一就是采用循环队列。