内容:主成分分析
- 介绍:
主成分分析是一种降维算法,它通过旋转和变换将多个指标转化为少数几个主成分,这些主成分是原变量的线性组合,且互不相关,其能反映出原始数据的大部分信息。

例如解决多重共线性问题
二.PCA的计算步骤
1.标准化处理(z标准化:减去均值除以标准差):
1.2.计算协方差矩阵:
1.3.计算相关系数矩阵R:

- 4计算R的特征值与特征向量:
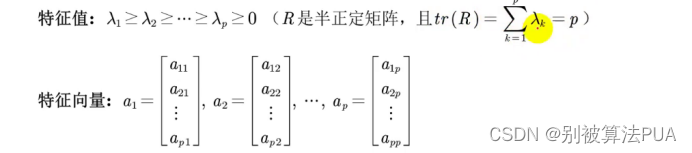
- 5计算主成分贡献率以及累计贡献率:

- 6通过累计贡献率写出主成分:

- 7 根据系数分析主成分代表的意义:

- 8后续分析:

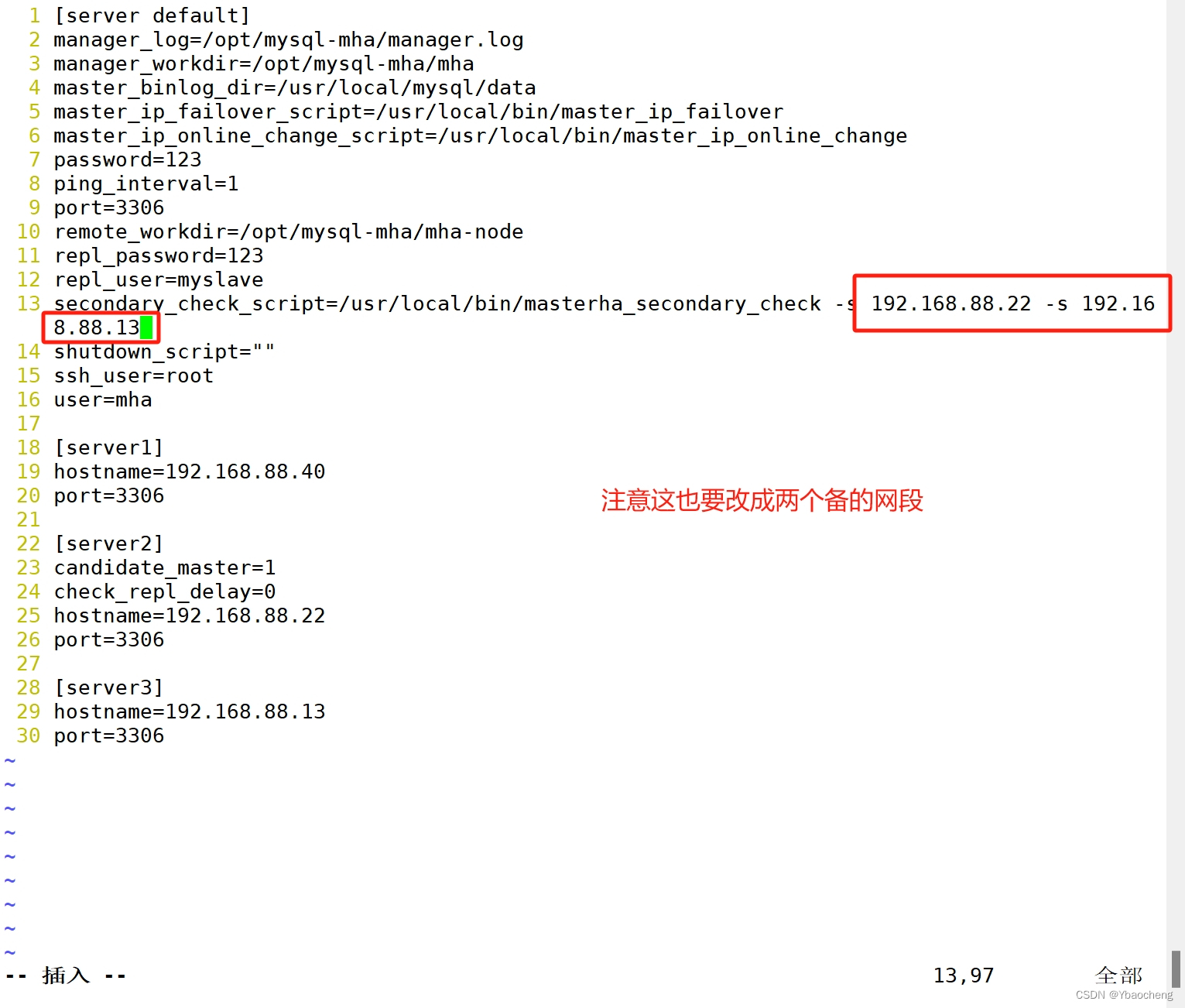
三.主成分分析的例题:
详细看视频,视频中讲解了如何对PCA使用MATLAB实现,以及如何分析获得的各种参数,数据等。
可以用于聚类

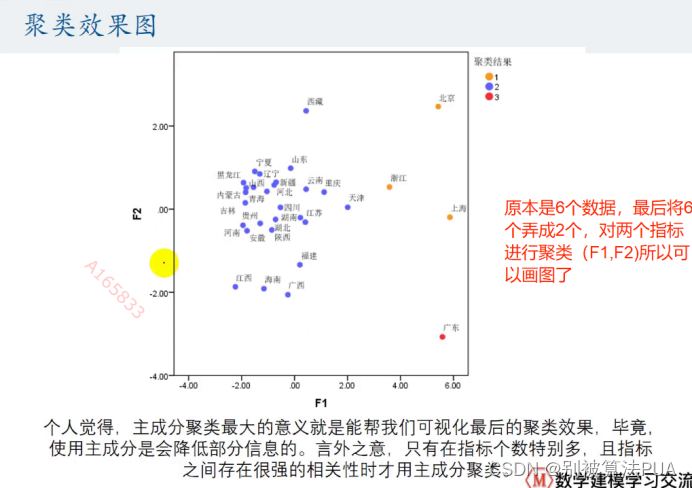
回归中解决多重共线性等,
之前用逐步回归解决多重共线性丢失的信息可能更多,所以我们可以使用以下的方法:

可总的来说:具体原视频分析我看懂了我感觉很妙,现在主要记住的就是,主成分分析可以用于降维,而具体降维肯定不是用来分析或评价某些东西的,一般都是用与某些算法之前,使用了降维之后对原算法有了更好的效果,在这里PCA就是如此,它主要可以应用于聚类与回归中