DS|哈夫曼编码及应用

题目一：DS树 -- 赫夫曼树的构建与编码

题目描述：

给定n个权值，根据这些权值构造huffman树，并进行huffman编码

注意数组访问是从位置1开始

要求：赫夫曼的构建中，默认左孩子权值不大于右孩子权值

输入要求：

第一行先输入n，表示有n个权值，即有n个叶子

第二行输入n个权值，权值全是小于1万的正整数

输出要求：

逐行输出每个权值对应的编码，格式如下：权值-编码
即每行先输出1个权值，再输出一个短划线，再输出对应编码

接着下一行输出下一个权值和编码，以此类推

输入样例：

5
15 4 4 3 2

输出样例：

15-1
4-010
4-011
3-001
2-000

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
using namespace std;#define MAXCODELEN	15
#define MAXHUFFMANCODENO 10
#define MAXCODESTRINGLEN 100typedef struct {int weight;int parent, lChild, rChild;char code[MAXCODELEN];
} HTNode, * HumffanTree;HTNode HT[2 * MAXHUFFMANCODENO];void Select(int pos, int* s1, int* s2) {int w1, w2, i;w1 = w2 = 100010;*s1 = *s2 = 0;for (i = 1; i <= pos; i++) {if (HT[i].weight < w1 && HT[i].parent == 0) {w2 = w1;*s2 = *s1;w1 = HT[i].weight;*s1 = i;}else if (HT[i].weight < w2 && HT[i].parent == 0) {w2 = HT[i].weight;*s2 = i;}}
}void CreateHuffmanTree(int n, int* w) {int m, s1, s2;m = 2 * n - 1;//为Huffman树的叶子结点赋值for (int i = 1; i <= n; i++) {HT[i].weight = w[i - 1];HT[i].parent = 0;HT[i].lChild = HT[i].rChild = 0;}//为Huffman的内部节点赋值for (int i = n + 1; i <= m; i++) {HT[i].weight = 0;HT[i].parent = HT[i].lChild = HT[i].rChild = 0;}for (int i = n + 1; i <= m; i++) {Select(i - 1, &s1, &s2);HT[s1].parent = i; HT[s2].parent = i;HT[i].lChild = s1; HT[i].rChild = s2;HT[i].weight = HT[s1].weight + HT[s2].weight;}
}void HuffmanCoding(int n){int j, m, c, f, start;// 存放每个字符的编码序列char cd[MAXCODELEN];m = MAXCODELEN;// 编码结束符cd[m - 1] = 0;for (int i = 1; i <= n; i++) {// 编码结束符位置start = m - 1;//从叶子到根逆向求每个字符的编码for (c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent) {if (HT[f].lChild == c) cd[--start] = '0';else cd[--start] = '1';}//将每个字符的Huffman编码存放起来for (j = 0; j < m - start; j++) HT[i].code[j] = cd[start + j];HT[i].code[j] = 0;}
}int main() {int n;cin >> n;int* array = new int[n];for (int i = 0; i < n; i++) cin >> array[i];CreateHuffmanTree(n, array);HuffmanCoding(n);for (int i = 1; i <= n; i++) {cout << HT[i].weight << "-" << HT[i].code << endl;}return 0;
}

题目二：DS树 -- 赫夫曼树解码

题目描述：

已知赫夫曼编码算法和程序，在此基础上进行赫夫曼解码

可以增加一个函数：int  Decode(const string codestr, char txtstr[]);//输入编码串codestr，输出解码串txtstr

该方法如果解码成功则返回1，解码失败则返回-1，本程序增加宏定义ok表示1，error表示-1

赫夫曼解码算法如下：

定义指针p指向赫夫曼树结点，指针i指向编码串，定义ch逐个读取编码串的字符

初始操作包括读入编码串str，设置p指向根结点，i为0表示指向串首，执行以下循环：

1）取编码串的第i个字符放入ch

2）如果ch是字符0，则p跳转到左孩子；如果ch是字符1，则p跳转到右孩子；如果ch非0非1，表示编码串有错误，报错退出

3）如果p指的结点是叶子，输出解码字符，p跳回根结点，i++，跳步骤1

4）如果p指的结点不是叶子且i未到编码串末尾，i++，跳步骤1

5）如果p指的结点不是叶子且i到达编码串末尾，报错退出

当i到达编码串末尾，解码结束。

输入要求：

第一行先输入n，表示有n个叶子

第二行输入n个权值，权值全是小于1万的正整数
第三行输入n个字母，表示与权值对应的字符
第四行输入k，表示要输入k个编码串
第五行起输入k个编码串

输出要求：

每行输出解码后的字符串，如果解码失败直接输出字符串“error”，不要输出部分解码结果

输入样例：

5
15 4 4 3 2
A B C D E
3
11111
10100001001
00000101100

输出样例：

AAAAA
ABEAD
error

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
using namespace std;#define MAXCODELEN	15
#define MAXHUFFMANCODENO 10
#define MAXCODESTRINGLEN 100typedef struct {char ch;int weight;int parent, lChild, rChild;char code[MAXCODELEN];
} HTNode, * HumffanTree;HTNode HT[2 * MAXHUFFMANCODENO];void Select(int pos, int* s1, int* s2) {int w1, w2, i;w1 = w2 = 100010;*s1 = *s2 = 0;for (i = 1; i <= pos; i++){if (HT[i].weight < w1 && HT[i].parent == 0){w2 = w1;*s2 = *s1;w1 = HT[i].weight;*s1 = i;}else if (HT[i].weight < w2 && HT[i].parent == 0){w2 = HT[i].weight;*s2 = i;}}
}void CreateHuffmanTree(int n, char* c, int* w) {int m, s1, s2;m = 2 * n - 1;//为Huffman树的叶子结点赋值for (int i = 1; i <= n; i++) {HT[i].ch = c[i - 1];HT[i].weight = w[i - 1];HT[i].parent = 0;HT[i].lChild = HT[i].rChild = 0;}//为Huffman的内部节点赋值for (int i = n + 1; i <= m; i++) {HT[i].weight = 0;HT[i].parent = HT[i].lChild = HT[i].rChild = 0;}for (int i = n + 1; i <= m; i++) {Select(i - 1, &s1, &s2);HT[s1].parent = i; HT[s2].parent = i;HT[i].lChild = s1; HT[i].rChild = s2;HT[i].weight = HT[s1].weight + HT[s2].weight;}
}void HuffmanCoding(int n)
{int j, m, c, f, start;// 存放每个字符的编码序列char cd[MAXCODELEN];m = MAXCODELEN;// 编码结束符cd[m - 1] = 0;for (int i = 1; i <= n; i++) {// 编码结束符位置start = m - 1;//从叶子到根逆向求每个字符的编码for (c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent) {if (HT[f].lChild == c) cd[--start] = '0';else cd[--start] = '1';}//将每个字符的Huffman编码存放起来for (j = 0; j < m - start; j++) HT[i].code[j] = cd[start + j];HT[i].code[j] = 0;}
}int ShowHuffmanDecode(int n, string str, string& st)
{int c, Root;Root = 2 * n - 1;c = Root;for (int i = 0; i < str.size(); i++) {if (str[i] == '0')c = HT[c].lChild;elsec = HT[c].rChild;if ((HT[c].lChild == 0) && (HT[c].rChild == 0)) {st += HT[c].ch;c = Root;}}if (HT[c].parent != 0) return 0;else return 1;
}int main() {int n;cin >> n;char* arr = new char[n];int* array = new int[n];for (int i = 0; i < n; i++) cin >> array[i];for (int i = 0; i < n; i++) cin >> arr[i];CreateHuffmanTree(n, arr, array);HuffmanCoding(n);int t;cin >> t;while (t--) {string s, st = "";cin >> s;if (!ShowHuffmanDecode(n, s, st)) cout << "error" << endl;else cout << st << endl;}return 0;
}

题目三：DS树 -- 带权路径和

题目描述：

二叉树的创建使用含空树表示的先序遍历序列，计算一棵二叉树的带权路径总和，即求赫夫曼树的带权路径和。

已知一棵二叉树的叶子权值，该二叉树的带权路径和WPL等于叶子权值乘于根节点到叶子的分支数，然后求总和。

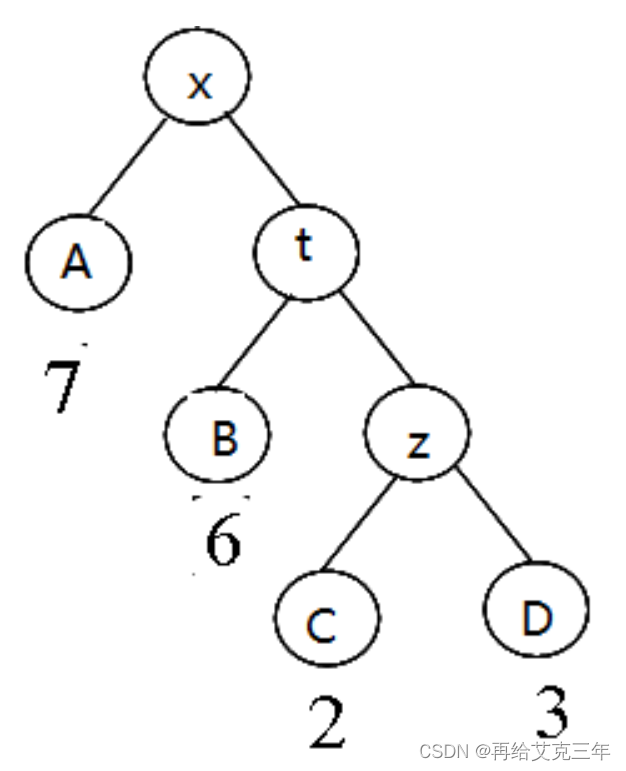
如下图中，叶子都用大写字母表示，权值对应为：A-7，B-6，C-2，D-3

树的带权路径和 = 7*1 + 6*2 + 2*3 + 3*3 = 34

输入要求：

第一行输入一个整数t，表示有t个二叉树

第二行输入一棵二叉树的先序遍历结果，空树用字符‘0’表示，注意输入全是英文字母和0，其中大写字母表示叶子

第三行先输入n表示有n个叶子，接着输入n个数据表示n个叶子的权值，权值的顺序和前面输入的大写字母顺序对应

以此类推输入下一棵二叉树

输出要求：

输出每一棵二叉树的带权路径和

输入样例：

2
xA00tB00zC00D00
4 7 6 2 3
ab0C00D00
2 10 20

输出样例：

34
40

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;struct BNode {char data;BNode* lChild;BNode* rChild;
};class BTree {
public:BNode* root;BTree() :root(NULL) {}BNode* creatBTree() {BNode* tmp;char ch;cin >> ch;if (ch == '0') tmp = NULL;else {tmp = new BNode;tmp->data = ch;tmp->lChild = creatBTree();tmp->rChild = creatBTree();}return tmp;}void CountWeight(BNode* cur, int level, int& sum) {int weight;if (cur != NULL) {if (cur->data >= 'A' && cur->data <= 'Z') {cin >> weight;sum += weight * level;}else{level++;CountWeight(cur->lChild, level, sum), CountWeight(cur->rChild, level, sum);}}}
};int main() {int t;cin >> t;while (t--) {int count = 0;BTree tree;tree.root = tree.creatBTree();int n;cin >> n;int sum = 0;tree.CountWeight(tree.root, 0, sum);cout << sum << endl;}return 0;
}

题目四：DS树 -- 二叉树之最大路径

题目描述：

给定一颗二叉树的逻辑结构（先序遍历的结果，空树用字符‘0’表示，例如AB0C00D00），建立该二叉树的二叉链式存储结构

二叉树的每个结点都有一个权值，从根结点到每个叶子结点将形成一条路径，每条路径的权值等于路径上所有结点的权值和。编程求出二叉树的最大路径权值。如下图所示，共有4个叶子即有4条路径，

路径1权值=5 + 4 + 11 + 7 = 27        路径2权值=5 + 4 + 11 + 2 = 22

路径3权值=5 + 8 + 13 = 26              路径4权值=5 + 8 + 4 + 1 = 18

可计算出最大路径权值是27。

该树输入的先序遍历结果为ABCD00E000FG00H0I00，各结点权值为：

A-5，B-4，C-11，D-7，E-2，F-8，G-13，H-4，I-1

输入要求：

第一行输入一个整数t，表示有t个测试数据

第二行输入一棵二叉树的先序遍历，每个结点用字母表示

第三行先输入n表示二叉树的结点数量，然后输入每个结点的权值，权值顺序与前面结点输入顺序对应

以此类推输入下一棵二叉树

输出要求：

每行输出每棵二叉树的最大路径权值，如果最大路径权值有重复，只输出1个

输入样例：

2
AB0C00D00
4 5 3 2 6
ABCD00E000FG00H0I00
9 5 4 11 7 2 8 13 4 1

输出样例：

11
27

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;struct BNode {char data;int weight;BNode* lChild;BNode* rChild;
};class BTree {
public:BNode* root;BTree() :root(NULL) {}BNode* creatBTree() {BNode* tmp;char ch;cin >> ch;if (ch == '0') tmp = NULL;else {tmp = new BNode;tmp->data = ch;tmp->lChild = creatBTree();tmp->rChild = creatBTree();}return tmp;}void Preorder(BNode* cur) {int weight;if (cur != NULL) {cin >> weight;cur->weight = weight;Preorder(cur->lChild), Preorder(cur->rChild);}}void addWeight(BNode* cur, int curWeight, int& maxWeight) {if (cur != NULL) {curWeight += cur->weight;if (cur->lChild == NULL && cur->rChild == NULL) maxWeight = max(maxWeight, curWeight);addWeight(cur->lChild, curWeight, maxWeight), addWeight(cur->rChild, curWeight, maxWeight);}}
};int main() {int t;cin >> t;while (t--) {int count = 0;BTree tree;tree.root = tree.creatBTree();int n;cin >> n;int maxWeight = 0;tree.Preorder(tree.root);tree.addWeight(tree.root, 0, maxWeight);cout << maxWeight << endl;}return 0;
}

题目五：DS树 -- 二叉树镜面反转

题目描述：

假设二叉树用二叉链表存储，用含空子树遍历的先序序列结果创建。空子树用字符#表示

输入二叉树的先序序列，请你先创建二叉树，并对树做个镜面反转，再输出反转后的二叉树的先序遍历、中序遍历、后序遍历和层序遍历的序列。所谓镜面反转，是指将所有非叶结点的左右孩子对换。

输入要求：

测试次数t

每组测试数据是一个二叉树的先序遍历序列，#表示空树

输出要求：

对每棵二叉树，输出镜面反转后的先序、中序、后序和层次遍历序列。如果空树，输出四个NULL（后面不加空格，每个NULL独自一行，中间没有空行）。如下：

NULL

NULL

NULL

NULL

输入样例：

3
41#32###65##7##
AB#C##D##
AB##C##

输出样例：

4 6 7 5 1 3 2 
7 6 5 4 3 2 1 
7 5 6 2 3 1 4 
4 6 1 7 5 3 2 
A D B C 
D A C B 
D C B A 
A D B C 
A C B 
C A B 
C B A 
A C B

代码示例：

#include <iostream>
#include <string>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;struct BNode {char data;BNode* lChild;BNode* rChild;
};class BTree {
public:BNode* root;BTree() :root(NULL) {}BNode* creatBTree() {BNode* tmp;char ch;cin >> ch;if (ch == '#') tmp = NULL;else {tmp = new BNode;tmp->data = ch;tmp->lChild = creatBTree();tmp->rChild = creatBTree();}return tmp;}void Preorder(BNode* cur) {if (cur != NULL) {cout << cur->data << " ";Preorder(cur->lChild), Preorder(cur->rChild);}}void Inorder(BNode* cur) {if (cur != NULL) {Inorder(cur->lChild);cout << cur->data << " ";Inorder(cur->rChild);}}void Postorder(BNode* cur) {if (cur != NULL) {Postorder(cur->lChild), Postorder(cur->rChild);cout << cur->data << " ";}}void levelDFSTree(BNode* cur) {queue<BNode*> Q;BNode* p = cur;if (p) Q.push(p);while (!Q.empty()) {p = Q.front();Q.pop();if (p) {cout << p->data << " ";Q.push(p->lChild), Q.push(p->rChild);}}}void Reverse(BNode* cur) {if (cur != NULL) {swap(cur->lChild, cur->rChild);Reverse(cur->lChild), Reverse(cur->rChild);}}
};int main() {int t;cin >> t;while (t--) {BTree tree;tree.root = tree.creatBTree();if (tree.root == NULL) {cout << "NULL" << endl << "NULL" << endl << "NULL" << endl << "NULL" << endl;}else{tree.Reverse(tree.root);tree.Preorder(tree.root);cout << endl;tree.Inorder(tree.root);cout << endl;tree.Postorder(tree.root);cout << endl;tree.levelDFSTree(tree.root);cout << endl;}}return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/323953.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

用LCD循环右移显示“Welcome to China“

用LCD循环右移显示“Welcome to China“

#include<reg51.h> //包含单片机寄存器的头文件 #include<intrins.h> //包含_nop_()函数定义的头文件 sbit RSP2^0; //寄存器选择位&#xff0c;将RS位定义为P2.0引脚 sbit RWP2^1; //读写选择位&#xff0c;将RW位定义为P2.1引脚 sbit EP2^2; //使能…
阅读更多...
数据分析-25-电商用户行为可视化分析

数据分析-25-电商用户行为可视化分析

文章目录 0. 数据代码获取1. 项目介绍1.1 分析背景1.2 分析目的1.3 分析思路 2. 数据清洗2.1 加载必要的库2.2 读取数据2.3 统计缺失值2.4 处理数据a. 删除重复值b. 转换时间格式c. 提取日期和时间d. 转换数据类型 3. 分析内容3.1 用户活跃规律a. 日均pv与uvb. 日新增pv、uv趋势…
阅读更多...
关于linux权限的相关操作

关于linux权限的相关操作

目录 文件的访问者 文件类型和访问权限 文件权限值的表示 文件访问权限的相关设置 目录的权限 粘滞位 总结 文件的访问者 文件和文件目录的所有者&#xff1a;u&#xff08;User&#xff09;文件和文件目录的所有者所在的组的用户&#xff1a;g&#xff08;Group&#…
阅读更多...
专业能力再获赞！棱镜七彩收到中国软件评测中心感谢信

专业能力再获赞！棱镜七彩收到中国软件评测中心感谢信

近日&#xff0c;中国软件评测中心&#xff08;工业和信息化部软件与集成电路促进中心&#xff09;发来感谢信&#xff0c;对棱镜七彩在助力信创产业发展过程中所做出的贡献表示感谢&#xff0c;并对棱镜七彩工作人员专业细致、尽职尽责的工作态度和敬业精神进行了高度赞扬。同…
阅读更多...
圆通速递单号查询入口，筛选出指定某天签收的单号

圆通速递单号查询入口，筛选出指定某天签收的单号

随着电商和物流行业的飞速发展&#xff0c;快递单号的管理也成了一个让人头疼的问题。如何快速筛选、整理这些快递单号&#xff0c;成为了提高生活和工作效率的关键。而【快递批量查询高手】的出现&#xff0c;正好可以巧妙的解决上面的问题&#xff0c;下面就来具体看看这款软…
阅读更多...
【AWS系列】巧用 G5g 畅游Android流媒体游戏

【AWS系列】巧用 G5g 畅游Android流媒体游戏

序言 Amazon EC2 G5g 实例由 AWS Graviton2 处理器提供支持&#xff0c;并配备 NVIDIA T4G Tensor Core GPU&#xff0c;可为 Android 游戏流媒体等图形工作负载提供 Amazon EC2 中最佳的性价比。它们是第一个具有 GPU 加速功能的基于 Arm 的实例。 借助 G5g 实例&#xff0c;游…
阅读更多...
HubSpot电子邮件：数字化时代的营销利器

HubSpot电子邮件：数字化时代的营销利器

在当今数字化时代&#xff0c;电子邮件仍然是企业与客户之间沟通的重要手段之一。而HubSpot电子邮件作为HubSpot全方位解决方案的一部分&#xff0c;不仅简化了营销流程&#xff0c;更为企业提供了强大的工具&#xff0c;助力建立更紧密的客户关系。本文将深入探讨HubSpot电子邮…
阅读更多...
系统安全及应用

系统安全及应用

1、基本安全措施 1.1、系统账号清理 在Linux系统中&#xff0c;除了用户手动创建的各种账号之外&#xff0c;还包括随系统或程序安装过程而生产的其他大量账号。除了超级用户root之外&#xff0c;其他大量账号只是用来维护系统运作、启动或保持服务进程&#xff0c;一般是不允…
阅读更多...
（三）STM32F407 cubemx串口中断通讯

（三）STM32F407 cubemx串口中断通讯

&#xff08;三&#xff09;STM32F407 cubemx串口中断通讯 这篇文章主要是个人的学习经验&#xff0c;想分享出来供大家提供思路&#xff0c;如果其中有不足之处请批评指正哈。废话不多说直接开始主题&#xff0c;本人是基于STM32F407VET6芯片&#xff0c;但是意在你看懂这篇文…
阅读更多...
数据结构学习 jz16 数值的整数次方

数据结构学习 jz16 数值的整数次方

关键词&#xff1a;快速幂 位运算 之前已经学过快速幂了&#xff0c;所以只是回忆。快速幂有递归版和非递归版。 题目&#xff1a; 这道题和之前的快速幂的区别是 n可能为负数。分类讨论即可。 思路&#xff1a; 区分正负&#xff1a; if (n < 0) return POW(1.0 / x, …
阅读更多...
电源测试系统与传统测试有什么不同？又有哪些突破？

电源测试系统与传统测试有什么不同？又有哪些突破？

电源测试系统是电源模块测试中非常常见的一种自动化测试软件&#xff0c;系统一般会将测试所需的仪器与软件集成到机柜中&#xff0c;这样方便对开关电源等产品进行批量化、自动化测试&#xff0c;那么电源测试系统是对比传统测试方法有哪些优势呢? 传统电源模块的测试一般都会…
阅读更多...
专业实习day3、4（路由器做内网访问公网）

专业实习day3、4（路由器做内网访问公网）

专业实习 代码 display ip interface brief 显示当前设备下所有接口IP undo IP地址支持覆盖&#xff0c;但是正常的命令不能覆盖必须undo&#xff08;删除&#xff09;掉 un in en 在做配置的过程中&#xff0c;设备系统一般都会出现一些提示或者告警之类的东西&#xff0c;从…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023