一款优秀的开源的工具能事倍功倍。今天给大家推荐的工具主要是Davide Faconti开发。该工具是基于QT开发，支持静态文件和实时数据流画图分析。以下是该工具的官网链接https://github.com/facontidavide/PlotJuggler。本人旨在介绍使用心得。

1.支持静态文件和实时数据流
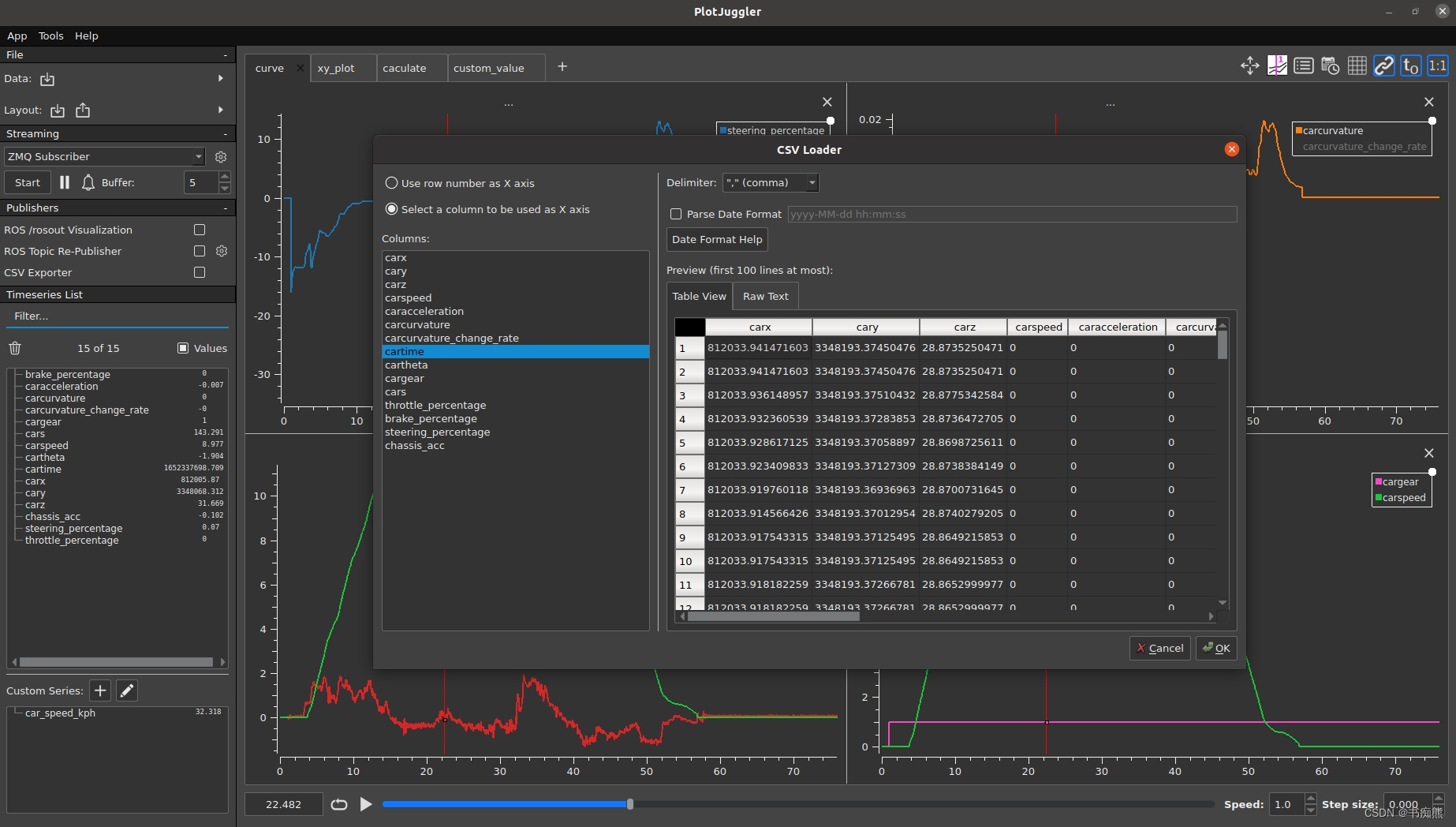
小技巧：可选择文件的row作为X axis,也可选择某colum作为X axis。选择选择某colum作为X axis的灵活性非常大，X axis可以设置为时间，频率，速度等。很好地满足了多元的工程需求。
加载csv文件和实时读取zmq消息


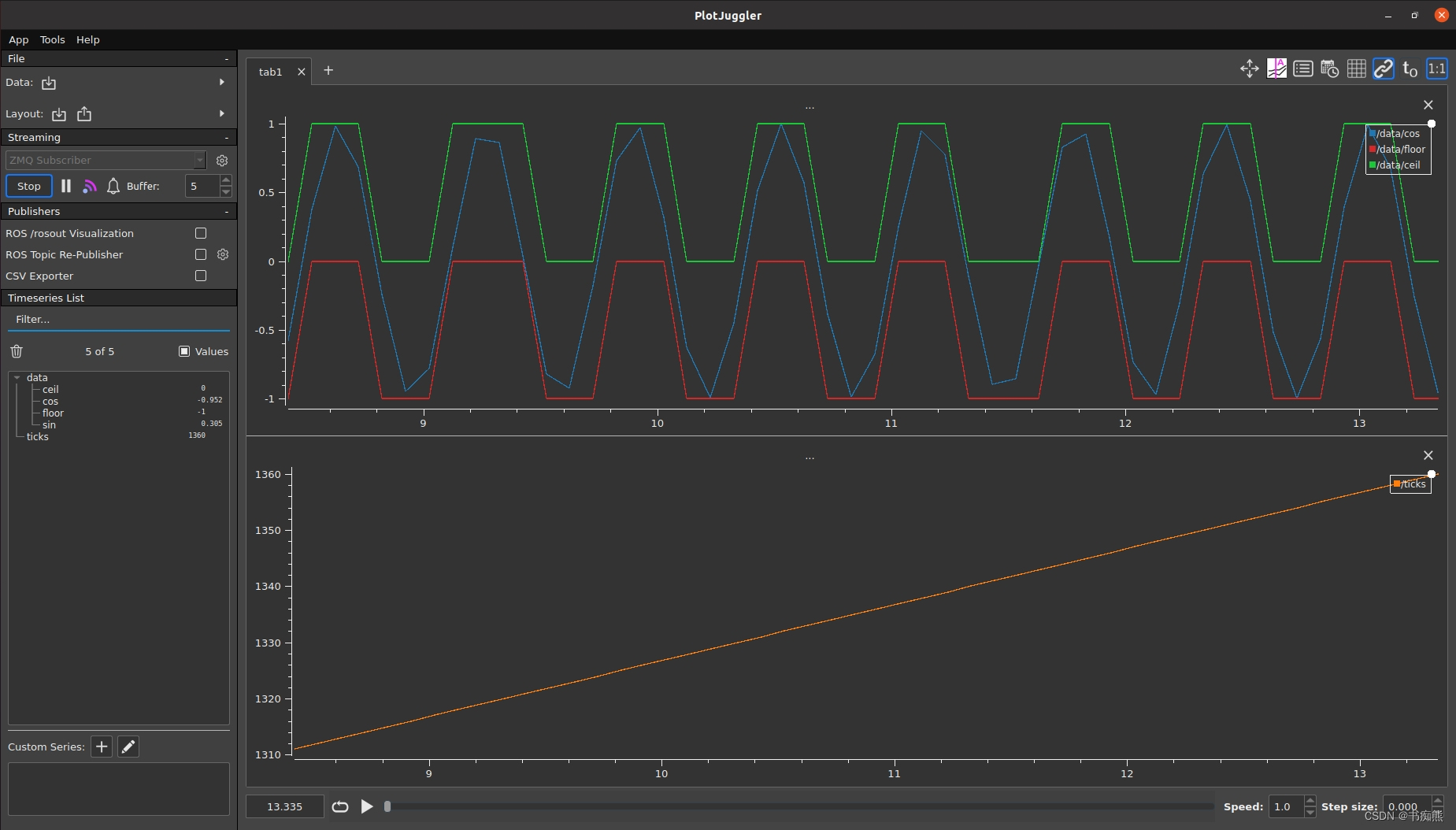
2.画出与X axis相关的曲线
小技巧：根据需求可以横纵向切割出多个视图，且可以在右上角选择是否要网格，是否需要所有窗口联动。很好地满足工程中分析多种数据之间关联。还可设置某条曲线为散点图，方便逐帧分析数据。


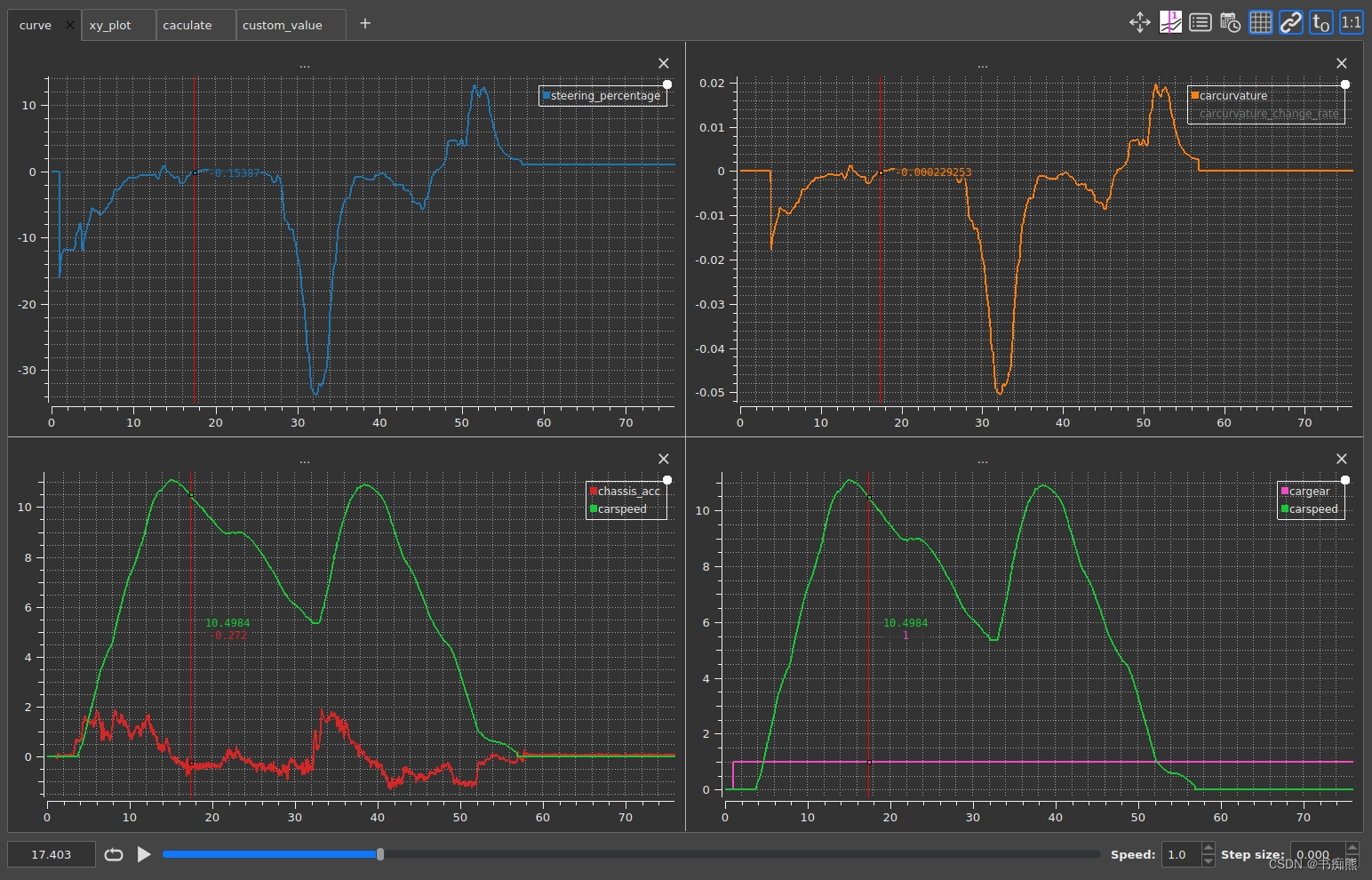
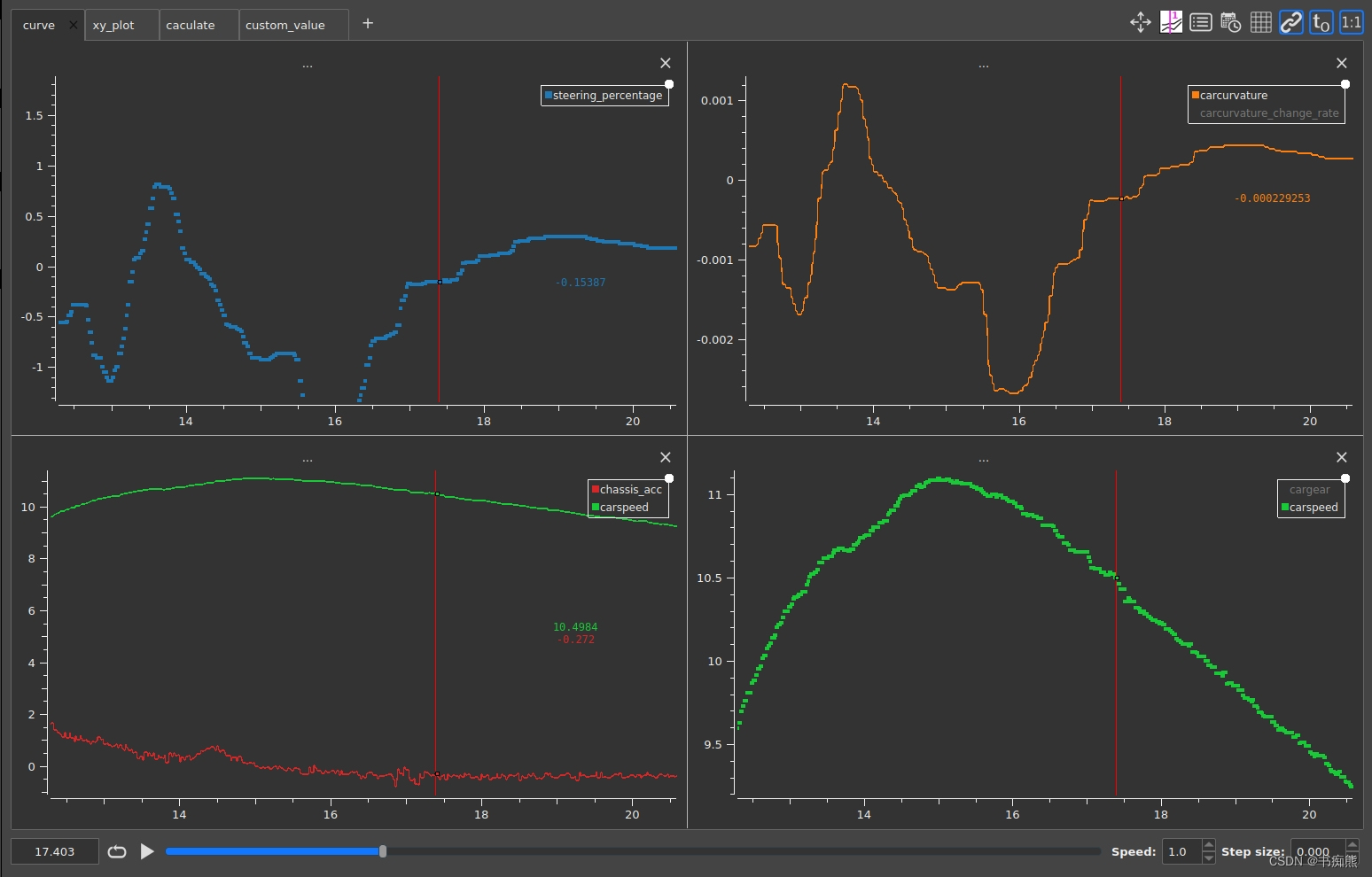
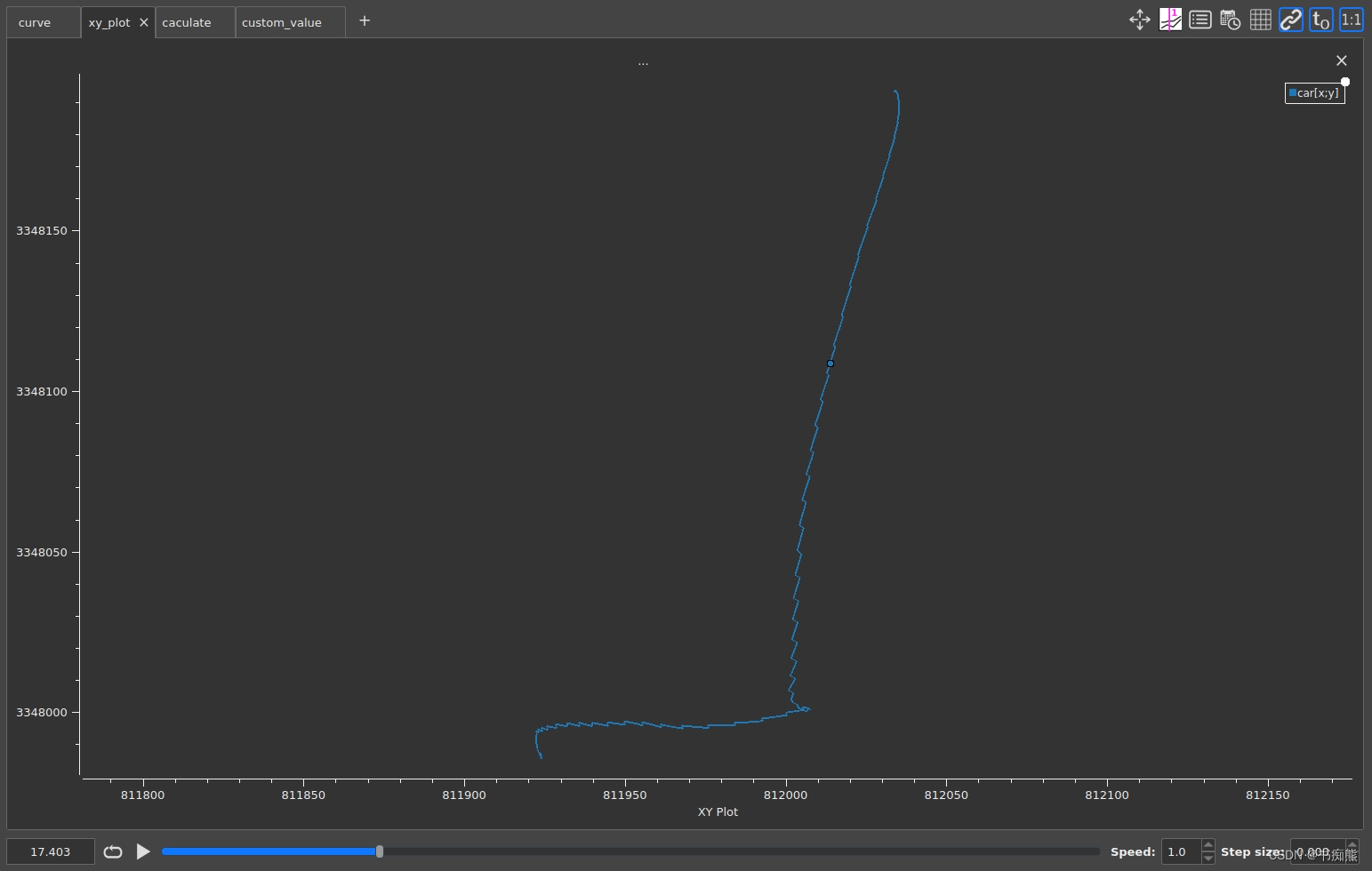
3.画与X-Y曲线
小技巧：无论上面X axis是什么含义，都可以使用XY-plot画图，如车辆的(x,y)坐标，整个工程的X axis可能是时间，如果想不改变X axis含义的情况下，画出轨迹图，就可使用XY-plot画图。

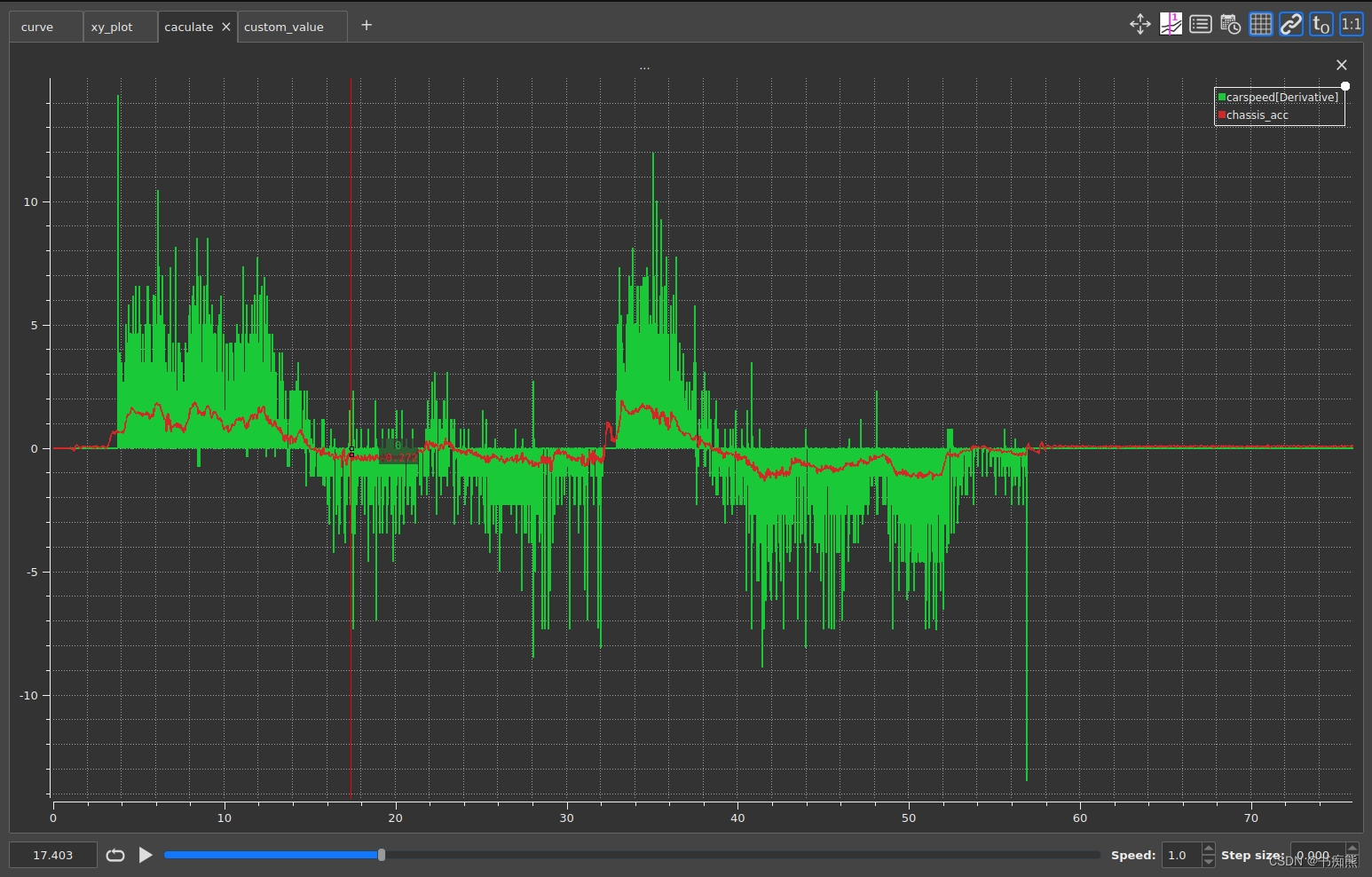
4.y=f(x)曲线
小技巧：PlotJuggler不仅仅是画图工具，还支持运算，甚至编程。可以对已知变量做函数运算。如下图，对速度carspeed求微分。ps：求微分的函数可以自己定义，默认的求微分函数效果并不好。

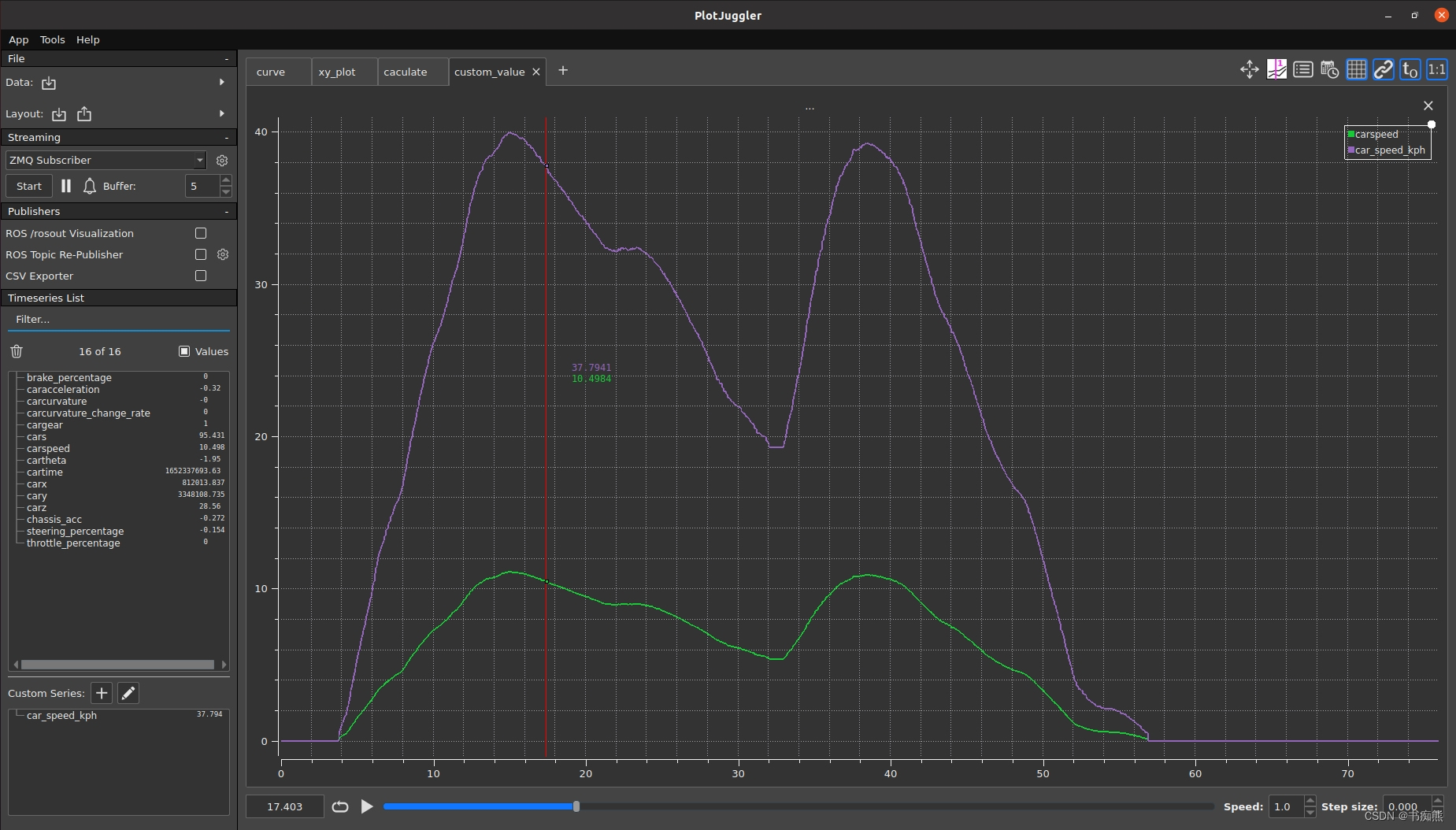
5.自定义曲线
小技巧：可以根据已知变量（单个或多个）构建出新变量。如下图，根据carspeed构建出单位为kph的car_speed_kph。这与y=f(x)曲线有点类似，但自定义曲线是新增了一个曲线。

结语
PlotJuggler工程非常强大，有兴趣的读者进参考官网学习。欢迎大家留言讨论。