本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你一个链表的头 head ，每个结点包含一个整数值。

在相邻结点之间，请你插入一个新的结点，结点值为这两个相邻结点值的 最大公约数 。

请你返回插入之后的链表。

两个数的 最大公约数 是可以被两个数字整除的最大正整数。

示例 1：

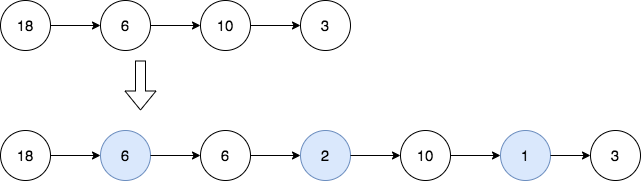
输入：head = [18,6,10,3]
输出：[18,6,6,2,10,1,3]
解释：第一幅图是一开始的链表，第二幅图是插入新结点后的图（蓝色结点为新插入结点）。
- 18 和 6 的最大公约数为 6 ，插入第一和第二个结点之间。
- 6 和 10 的最大公约数为 2 ，插入第二和第三个结点之间。
- 10 和 3 的最大公约数为 1 ，插入第三和第四个结点之间。
所有相邻结点之间都插入完毕，返回链表。

示例 2：

输入：head = [7]
输出：[7]
解释：第一幅图是一开始的链表，第二幅图是插入新结点后的图（蓝色结点为新插入结点）。
没有相邻结点，所以返回初始链表。

提示：

• 链表中结点数目在 [1, 5000] 之间。
• 1 <= Node.val <= 1000

---

解法 迭代

遍历链表，在当前节点 $\text{cur}$ 后面插入 $gcd$ 节点，同时 $\text{gcd}$ 节点指向 $\text{cur}$ 的下一个节点。插入后，$\text{cur}$ 更新为 $\text{cur}.\text{next}.\text{next}$ ，也就是 $cur$ 原来的下一个节点，开始下一轮循环。循环直到 $cur$ 没有下一个节点为止。

// cpp
class Solution {
public:ListNode* insertGreatestCommonDivisors(ListNode* head) {for (auto cur = head; cur->next; cur = cur->next->next)cur->next = new ListNode(gcd(cur->val, cur->next->val), cur->next);return head;}
};
// java
class Solution {public ListNode insertGreatestCommonDivisors(ListNode head) {for (ListNode cur = head; cur.next != null; cur = cur.next.next) {cur.next = new ListNode(gcd(cur.val, cur.next.val), cur.next);}return head;}private int gcd(int a, int b) { while (a != 0) {int t = a;a = b % a;b = t;}return b;}
}
// python
class Solution:def insertGreatestCommonDivisors(self, head: Optional[ListNode]) -> Optional[ListNode]:cur = headwhile cur.next:cur.next = ListNode(gcd(cur.val, cur.next.val), cur.next)cur = cur.next.nextreturn head
// go
/*** Definition for singly-linked list.* type ListNode struct {*     Val int*     Next *ListNode* }*/
func insertGreatestCommonDivisors(head *ListNode) *ListNode {for cur := head; cur.Next != nil; cur = cur.Next.Next {cur.Next = &ListNode{gcd(cur.Val, cur.Next.Val), cur.Next}}return head
}
func gcd(a, b int) int {for a != 0 {a, b = b % a, a}return b
}
// rust
// Definition for singly-linked list.
// #[derive(PartialEq, Eq, Clone, Debug)]
// pub struct ListNode {
//   pub val: i32,
//   pub next: Option<Box<ListNode>>
// }
//
// impl ListNode {
//   #[inline]
//   fn new(val: i32) -> Self {
//     ListNode {
//       next: None,
//       val
//     }
//   }
// }
impl Solution {pub fn insert_greatest_common_divisors(mut head: Option<Box<ListNode>>) -> Option<Box<ListNode>> {let mut cur = &mut head;while cur.as_ref().unwrap().next.is_some() {let x = cur.as_mut().unwrap();let next = x.next.take();x.next = Some(Box::new(ListNode {val: Self::gcd(x.val, next.as_ref().unwrap().val),next,}));cur = &mut cur.as_mut().unwrap().next.as_mut().unwrap().next;}head}fn gcd(mut a: i32, mut b: i32) -> i32 {while a != 0 {(a, b) = (b % a, a);}b}
}

复杂度分析：

• 时间复杂度：$\mathcal{O}(n\log U)$ ，其中 $n$ 为链表长度，$U$ 为节点值的最大值。每次计算 $gcd$ 需要 $\mathcal{O}(\log U)$ 的时间。
• 空间复杂度：$\mathcal{O}(1)$ 。返回值的空间不计入。