20240105-工作安排的最大收益-编程知识

20240105-工作安排的最大收益

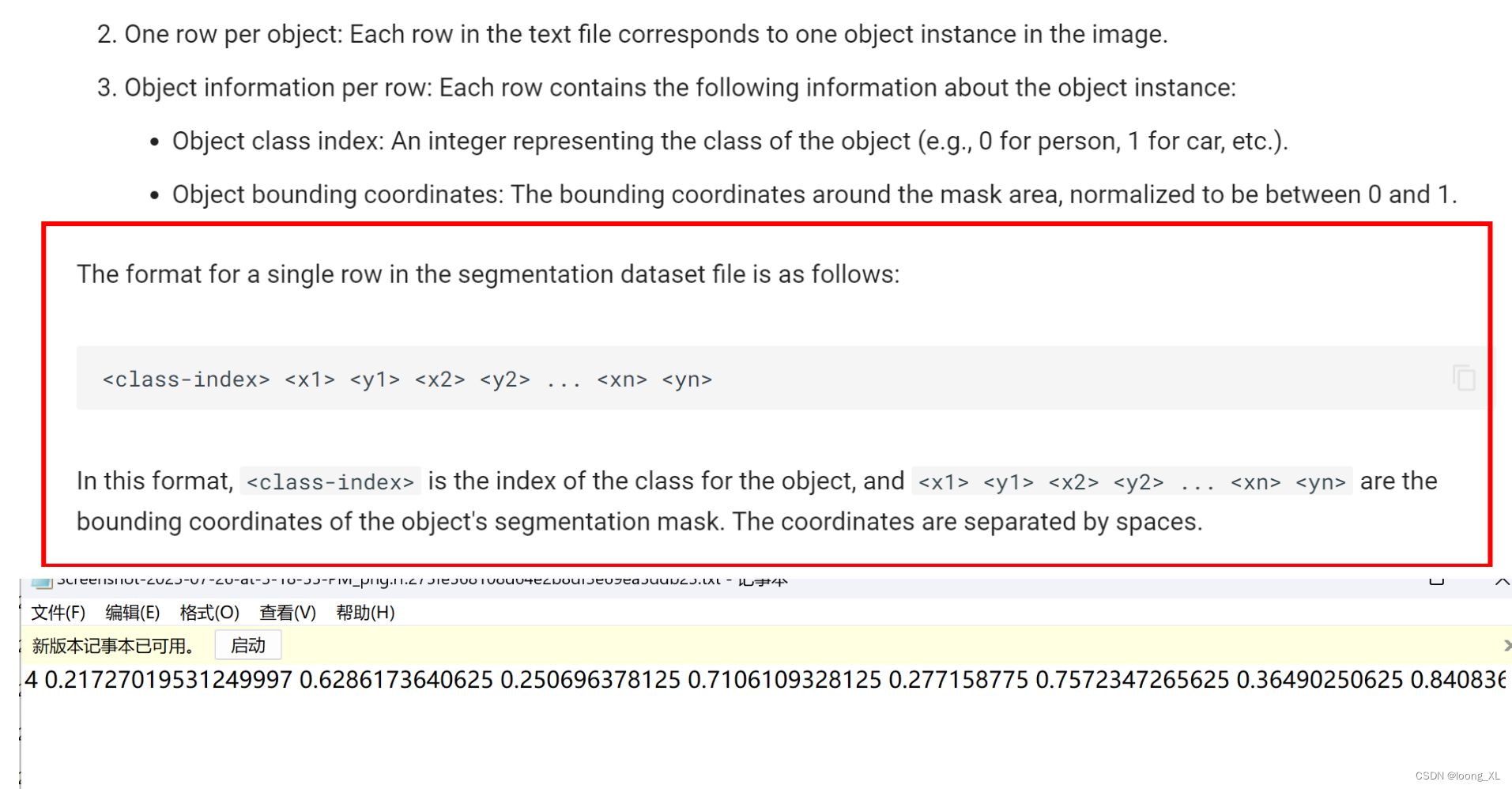
题目要求

我们有 n 份工作，每份工作都安排在 startTime[i] 至 endTime[i] 期间完成，从而获得 profit[i] 的利润。

给你 startTime、endTime 和 profit 数组，返回你能获得的最大利润，使得子集中没有两个时间范围重叠的工作。

如果你选择了一项在 X 时间结束的工作，你就可以开始另一项在 X 时间开始的工作。

例子

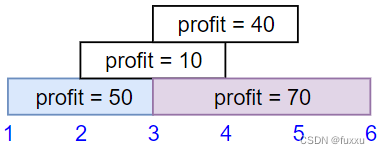
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

思路

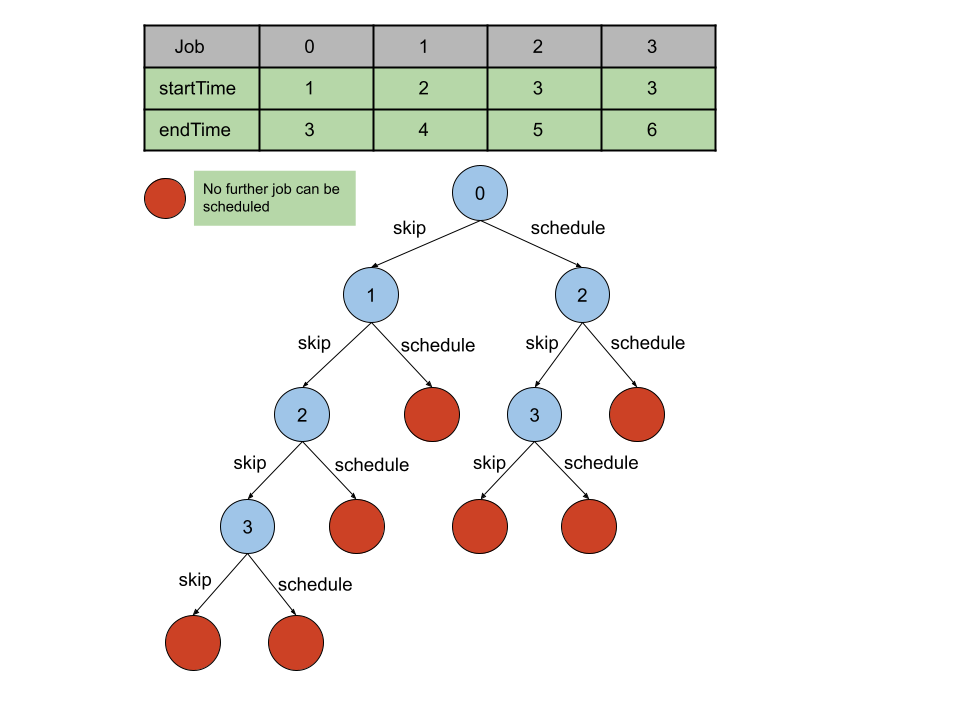
这个题目看起来似乎是一个递归问题（背包），在有限的时间内放下最多的工作（产生最大的价值？）但是仔细一想每个工作由起始结束时间决定，并不仅仅是工作时长的大小（可以直接放到背包中）。因此我又想是否使用深度优先搜索解决这个问题。似乎可行...

这次的深度优先搜索需要遍历所有的可能情况，然后返回最优的profit值。

终止条件

那么深搜的终止条件是什么，显而易见就是最后一个工作的截至时间之后，不能再有其他的工作，即：

if (当前工作的截止时间之后没有其他工作) {maxprofit = max(profit, maxprofit);return;}

bool hasNext = false;for (int i = start + 1; i < startTime.size(); ++i) {if (endTime[start] < startTime[i]) {hasNext = true;break;}}if (!hasNext) {maxprofit = max(maxprofit, currentProfit);return;}

回溯

for (int i = start; i < startTime.size(); ++i) {currentProfit += profit[i];backtracking(i+1, currentProfit, startTime, endTime, profit);currentProfit -= profit[i];}

目前已经完成了回溯：深搜（其实好像不太能抽象成一棵树）算法，但是目前还没有正确的处理时间冲突（即i+1的部分），修改后代码如下，

class Solution {
public:int maxprofit = -1;void backtracking(int startIndex, int lastEnd, int currentProfit, const vector<int>& startTime, const vector<int>& endTime, const vector<int>& profit) {// bool hasNext = false;// for (int i = 0; i < startTime.size(); ++i) {//     if (lastEnd < startTime[i]) {//         hasNext = true;//         break;//     }// }// if (!hasNext) {//     maxprofit = max(maxprofit, currentProfit);//     return;// }maxprofit = max(maxprofit, currentProfit);for (int i = startIndex; i < startTime.size(); ++i) {if (startTime[i] < lastEnd) {continue;}currentProfit += profit[i];printf("Position: %d, currentProfit: %d, maxProfit: %d", i, currentProfit, maxprofit);backtracking(i+1, endTime[i], currentProfit, startTime, endTime, profit);currentProfit -= profit[i];}}int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {int n = startTime.size();vector<int> jobs(n);iota(jobs.begin(), jobs.end(), 0); // 填充索引// 根据 startTime 排序索引sort(jobs.begin(), jobs.end(), [&](int a, int b) {return startTime[a] < startTime[b];});// 重新排列 startTime、endTime 和 profitvector<int> sortedStartTime(n), sortedEndTime(n), sortedProfit(n);for (int i = 0; i < n; ++i) {sortedStartTime[i] = startTime[jobs[i]];sortedEndTime[i] = endTime[jobs[i]];sortedProfit[i] = profit[jobs[i]];}backtracking(0, -1, 0, sortedStartTime, sortedEndTime, sortedProfit);return maxprofit;}
};

结果是超时了。

重新寻找另外的思路，

思路还是类似的，不过转而采用动态规划。

class Solution {
public:int memo[50001];int findMaxProfit(vector<vector<int>>& jobs, vector<int>& start, int n, int position) {if (position == n) {return 0;}if (memo[position] != -1) {return memo[position];}int nextIndex = lower_bound(start.begin(), start.end(), jobs[position][1]) - start.begin();int maxProfit = max(findMaxProfit(jobs, start, n, position+1),jobs[position][2] + findMaxProfit(jobs, start, n, nextIndex));return memo[position] = maxProfit;}int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {vector<vector<int>> jobs;memset(memo, -1, sizeof(memo));for (int i = 0; i < profit.size(); ++i) {jobs.push_back({startTime[i], endTime[i], profit[i]});}sort(jobs.begin(), jobs.end());for (int i = 0; i < profit.size(); ++i) {startTime[i] = jobs[i][0];}return findMaxProfit(jobs, startTime, profit.size(), 0);}
};

状态转移方程：

maxProfit = max(findMaxProfit(..., position+1), jobs[position][2] + findMaxProfit(..., nextIndex))
这个方程表示当前最大利润是两种选择中的较大值：要么跳过当前工作（只考虑下一个工作，即position+1），要么选择当前工作（当前工作的利润加上从nextIndex开始的后续工作的最大利润）。

复杂度分析：