C#，深度优先搜索（DFS）、广度优先搜索（BFS）算法的源代码与数据可视化-编程知识

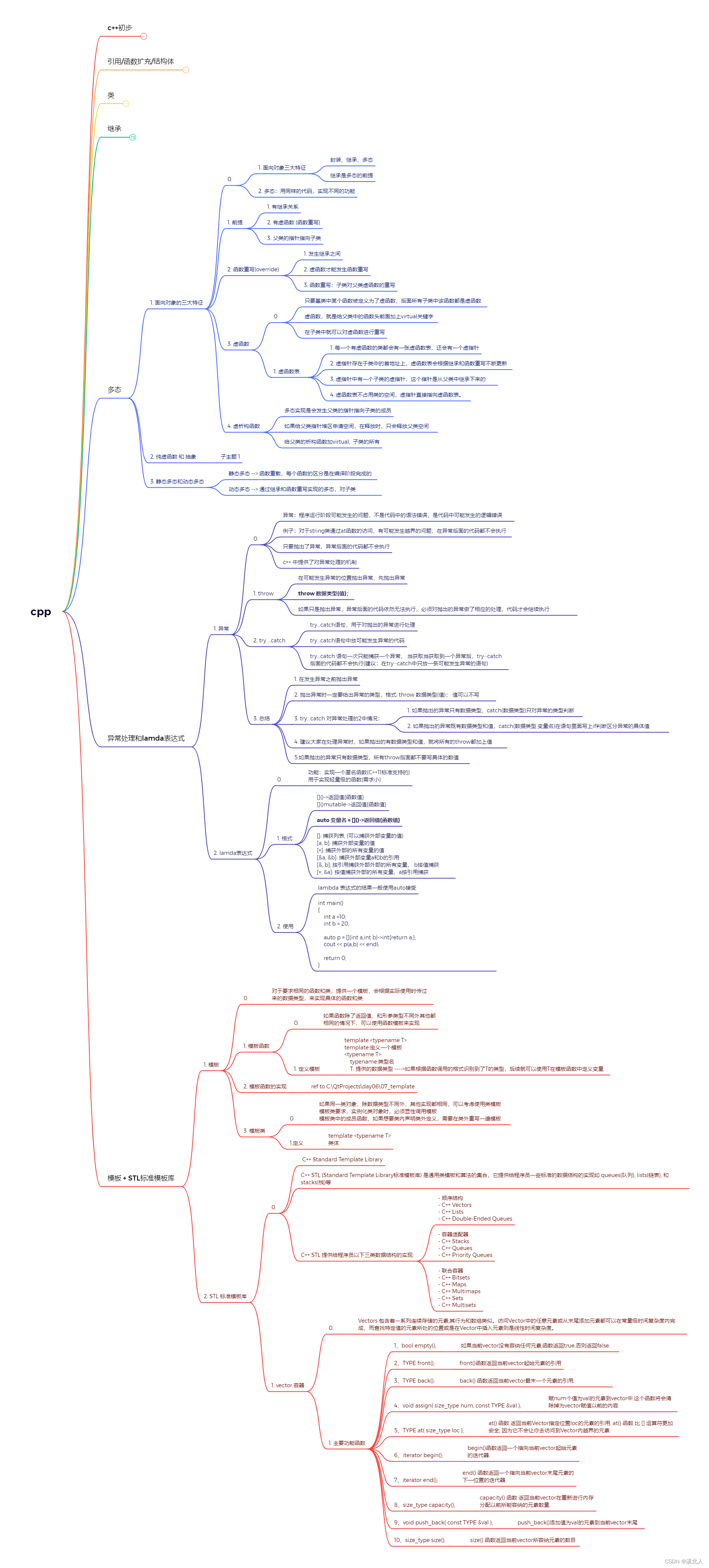
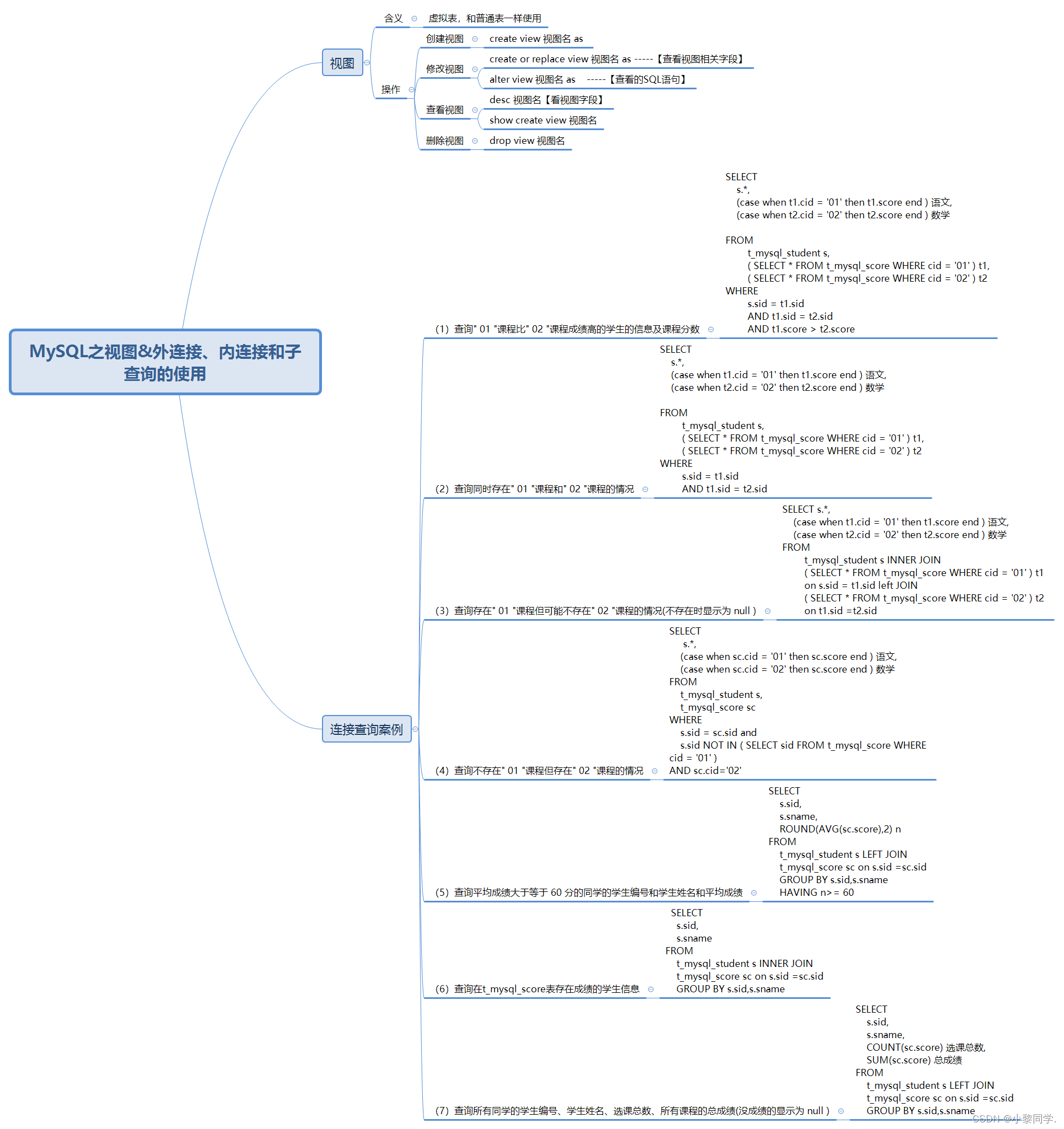
概述

下载源代码：

链接：https://pan.baidu.com/s/1sLxMT78LVg2dWyXXFvM--w?pwd=2kwl 提取码：2kwl --来自百度网盘超级会员V5的分享https://pan.baidu.com/s/1sLxMT78LVg2dWyXXFvM--w?pwd=2kwl

深度优先搜索（亦称深度优先遍历，Deep First Search，简称DFS），广度优先搜索（亦称广度优先遍历，Breadth First Search，简称BFS）都是很基础的算法，也是大家很熟悉的。

先看一下可视化的效果。

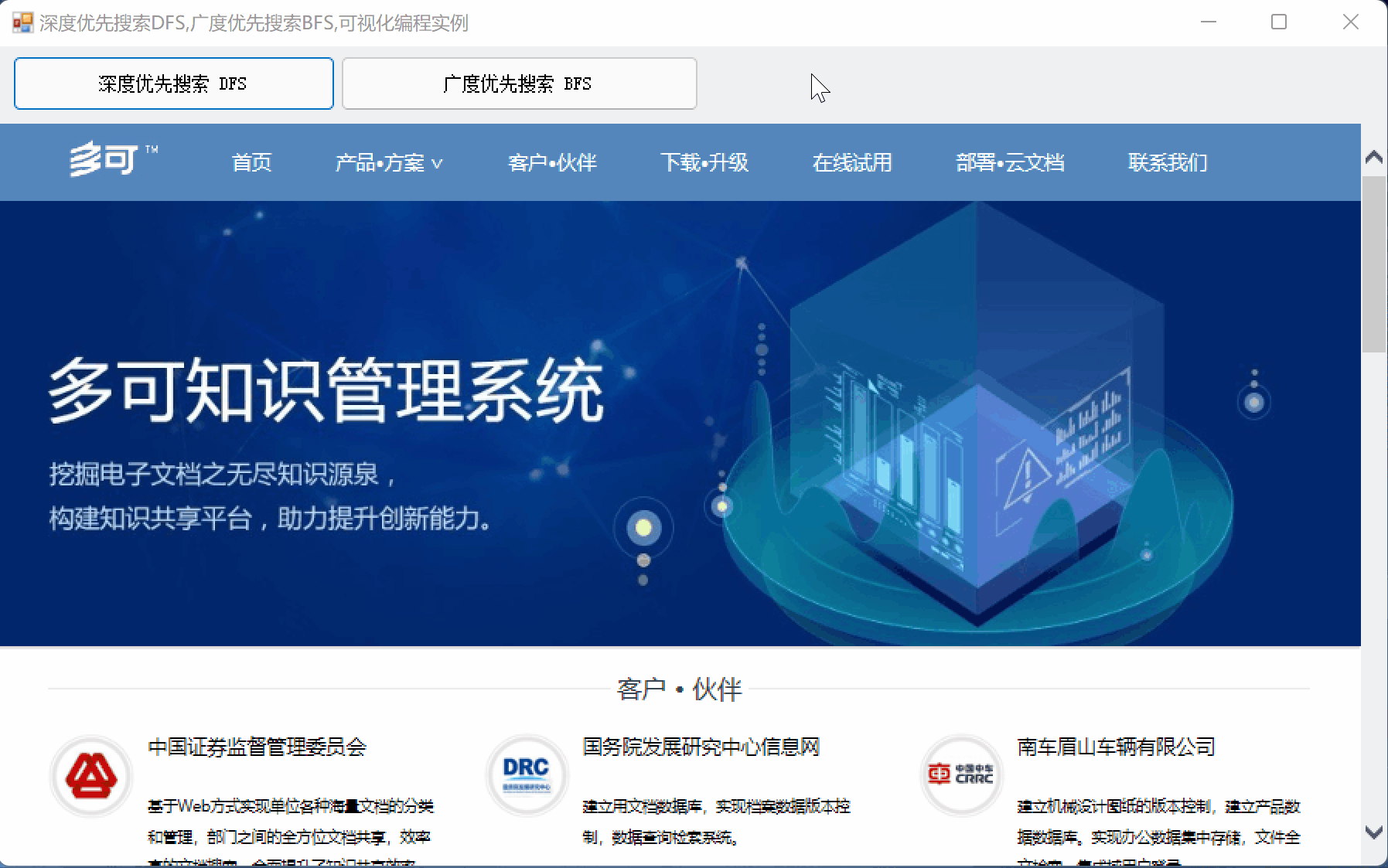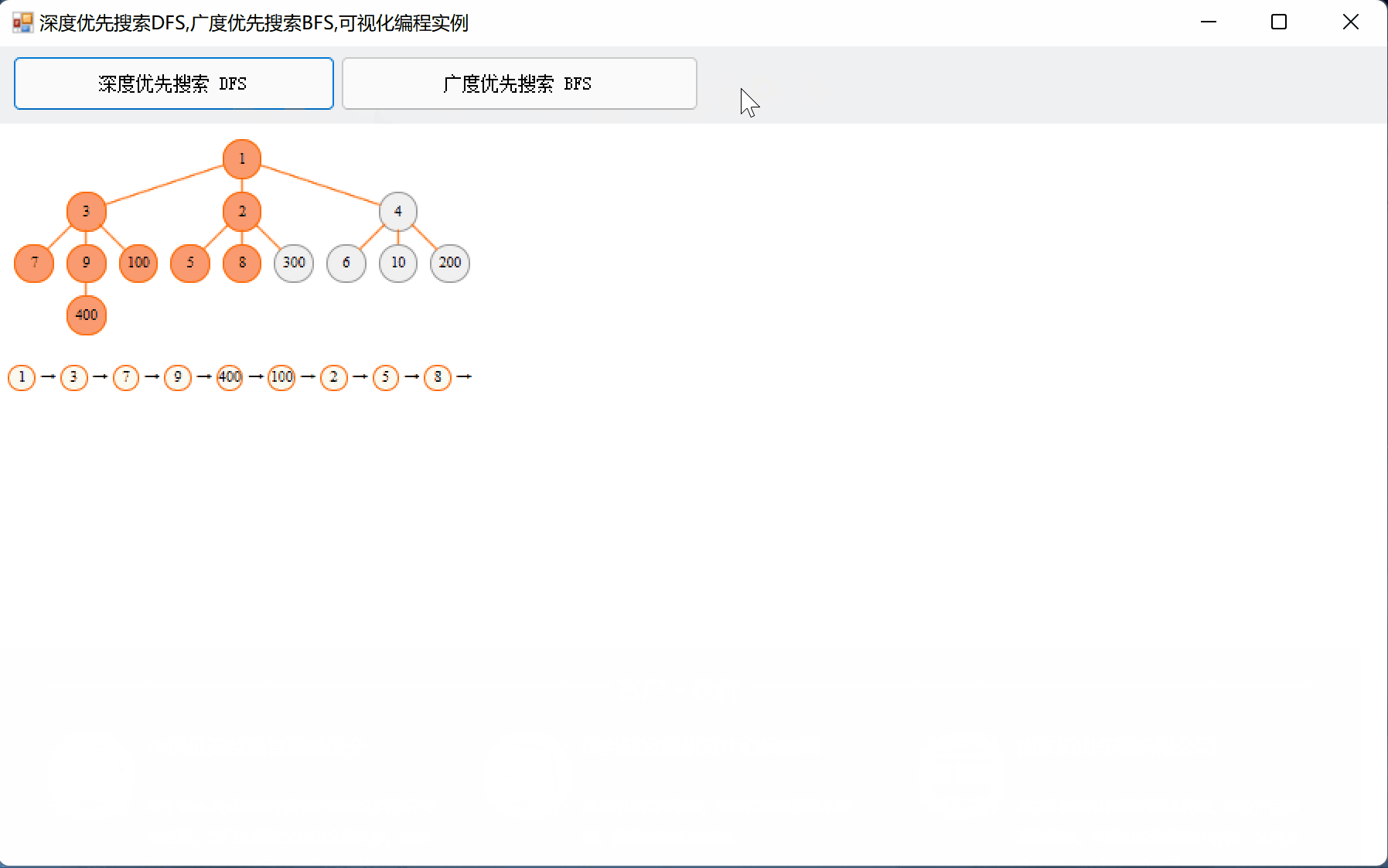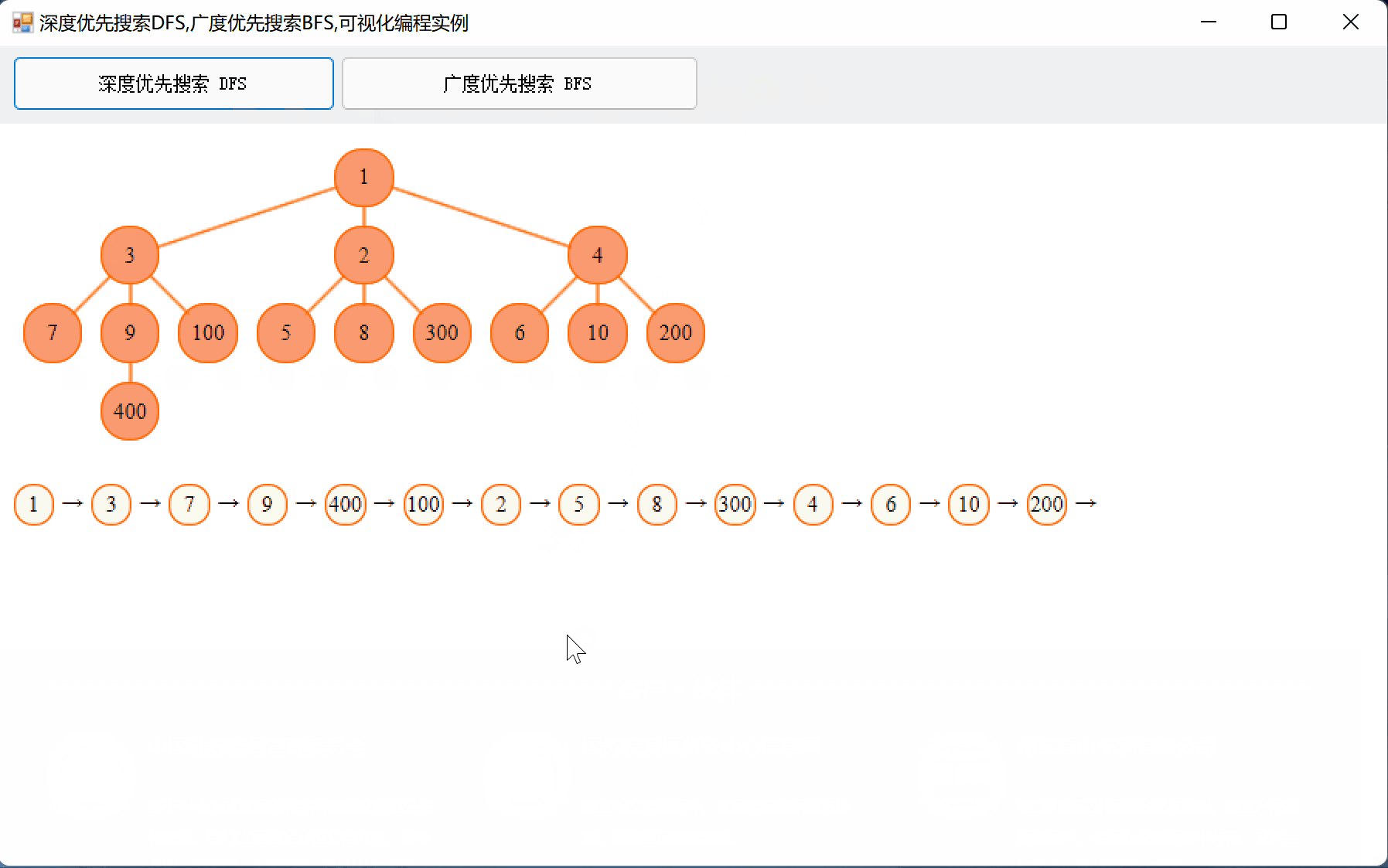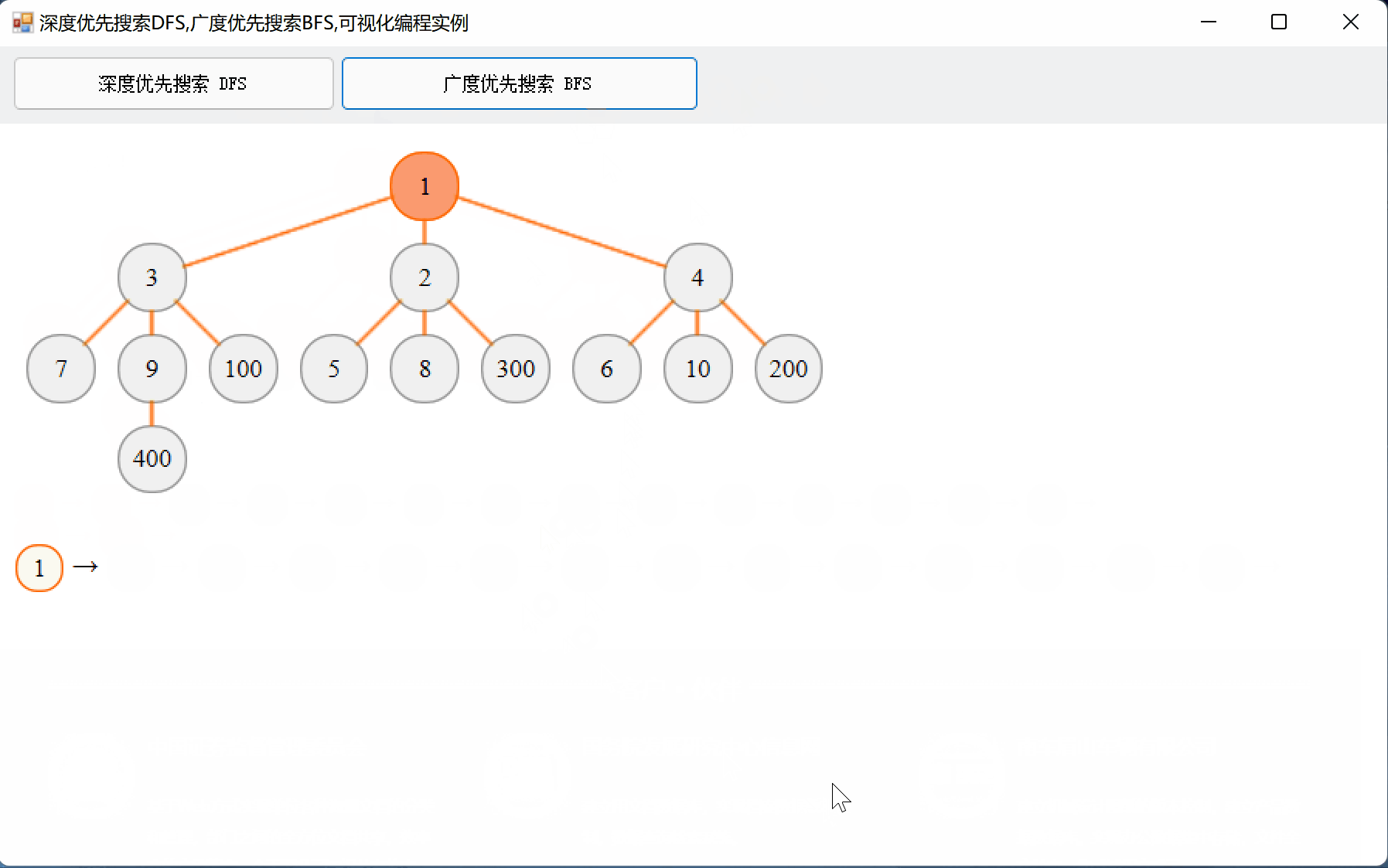
一、DFS,BFS的基本概念

摘自：明引树的广度优先遍历与深度优先遍历算法_明引的博客-CSDN博客_深度遍历和广度遍历算法1 树的广度优先搜索算法广度优先搜索算法（Breadth First Search），又叫宽度优先搜索，或横向优先搜索。是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。如上图所示的二叉树，A 是第一个访问的，然后顺序是 B、C，然后再是 D、E、F、G。那么，怎样才能来保证这个访问的顺序呢？借助队列数据结构，由于队列是先进先出的顺序，因此可以先https://blog.csdn.net/lmingyin5/article/details/47282925

广度优先遍历算法，又叫宽度优先遍历，或横向优先遍历，是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

深度优先遍历算法是遍历算法的一种。是沿着树的深度遍历树的节点。

当节点v的所有边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。

如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

摘自：小枫学IT https://blog.csdn.net/EngineerofAI/article/details/120590420广度优先搜索算法类似于二叉树的层序遍历，是一种分层的查找过程，每向前一步可能访问一批顶点，没有回退的情况，因此不是一个递归的算法。首先访问起始顶点v，接着由v出发，依存访问v的各个未访问过的邻接顶点w1，w2，…，wi，然后依次访问w1，w2，…，wi的所有未被访问过的邻接顶点；再从这些访问过的顶点出发，访问它们所有未被访问过的邻接顶点······依次类推，直到图中所有顶点都被访问过为止。

与广度优先搜索不同，深度优先搜索（Depth-First-Search，DFS）类似于树的先序遍历。过程：从一个顶点V0开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底，直到所有顶点被全部走完，这种尽量往深处走的概念即是深度优先的概念。

二、DFS,BFS的C#实现

摘自： csdnBigBoy

代码可用，注释清晰全面，大家可以仔细阅读。

三、DFS,BFS的可视化实现

学生经常问，什么样的程序是好程序？最基本的就是：

（1）好读：程序要便于阅读；注释合理；格式化；

（2）好看：程序逻辑、思路清晰、模块与板块划分合理；命名规则一致；

（3）好用：运行正常；稳定第一、性能第二；

因此，程序的运行结果能及时被看到！程序可视化是重要的一种形式。

先看看效果：

上代码（改编自csdnBigBoy的代码）：

using System;
using System.Text;
using System.Linq;
using System.Data;
using System.Collections;
using System.Collections.Generic;
using System.Windows.Forms;namespace DFSBFS
{public partial class Form1 : Form{TreeInfo TreeTotal = null;List<NodeInfo> PathResult = null;public Form1(){InitializeComponent();}private void Form1_Load(object sender, EventArgs e){this.Text = "深度优先搜索算法DFS,广度优先搜索算法BFS,可视化编程实例";button1.Text = "深度优先搜索算法 DFS"; button1.Cursor = Cursors.Hand;button2.Text = "广度优先搜索算法 BFS"; button2.Cursor = Cursors.Hand;panel1.Dock = DockStyle.Top; panel2.Dock = DockStyle.Fill;webBrowser1.Navigate("http://www.315soft.com");}private static TreeInfo TreeGrowth(){TreeInfo tree = new TreeInfo();tree.Append(new NodeInfo(1, new int[] { 3, 2, 4 }));tree.Append(new NodeInfo(2, new int[] { 1, 5, 8, 300 }));tree.Append(new NodeInfo(3, new int[] { 1, 7, 9, 100 }));tree.Append(new NodeInfo(4, new int[] { 1, 6, 10, 200 }));tree.Append(new NodeInfo(5, new int[] { 2 }));tree.Append(new NodeInfo(6, new int[] { 4 }));tree.Append(new NodeInfo(7, new int[] { 3 }));tree.Append(new NodeInfo(8, new int[] { 2 }));tree.Append(new NodeInfo(9, new int[] { 3, 400 }));tree.Append(new NodeInfo(10, new int[] { 4 }));tree.Append(new NodeInfo(100, new int[] { 3 }));tree.Append(new NodeInfo(200, new int[] { 4 }));tree.Append(new NodeInfo(300, new int[] { 2 }));tree.Append(new NodeInfo(400, new int[] { 9 }));return tree;}/// <summary>/// 深度优先搜索算法/// Deep First Search Algorithm/// </summary>/// <param name="Tree"></param>/// <param name="startNode"></param>private static List<NodeInfo> DFS(TreeInfo Tree, NodeInfo startNode){// 详细注解请浏览原文// https://blog.csdn.net/CSDNBigBoy/article/details/80635220List<NodeInfo> path = new List<NodeInfo>();path.Add(startNode);List<NodeInfo> b = new List<NodeInfo>();b.Add(startNode);startNode.Visited = true;NodeInfo a = new NodeInfo();while (b.Count != 0){List<NodeInfo> b_nbs = Tree.FindNeighbors(b[b.Count - 1]);a = b_nbs.FirstOrDefault(k => !k.Visited);while (a != null){b.Add(a);path.Add(a);a.Visited = true;b_nbs = Tree.FindNeighbors(b[b.Count - 1]);a = b_nbs.FirstOrDefault(k => !k.Visited);}if (a == null){b.Remove(b[b.Count - 1]);}}return path;}/// <summary>/// 广度优先搜索算法/// Breadth First Search Algorithm/// </summary>/// <param name="Tree"></param>/// <param name="startNode"></param>private static List<NodeInfo> BFS(TreeInfo Tree, NodeInfo startNode){// 详细注解请浏览原文// https://blog.csdn.net/CSDNBigBoy/article/details/80635220List<NodeInfo> path = new List<NodeInfo>();path.Add(startNode);Queue qq = new Queue();qq.Enqueue(startNode);startNode.Visited = true;NodeInfo a = new NodeInfo();while (qq.Count != 0){a = (NodeInfo)qq.Dequeue();List<NodeInfo> a_nbs = Tree.FindNeighbors(a);foreach (NodeInfo tmp in a_nbs.Where(k => !k.Visited).ToList()){qq.Enqueue(tmp);path.Add(tmp);tmp.Visited = true;}}return path;}private string ShowPath(){StringBuilder sb = new StringBuilder();sb.AppendLine("<!DOCTYPE html PUBLIC \"-//W3C//DTD XHTML 1.0 Transitional//EN\" \"http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd\">");sb.AppendLine("<html xmlns=\"http://www.w3.org/1999/xhtml\" >");sb.AppendLine("<head>");sb.AppendLine("<style>");sb.AppendLine(".ball1 { width:30px;height:30px;font-size:12px;line-height:30px;border:solid 1px #999999;background-color:#F0F0F0;text-align:center;border-radius:15px; }");sb.AppendLine(".ball2 { width:30px;height:30px;font-size:12px;line-height:30px;border:solid 1px #FF6701;background-color:#FA9A70;text-align:center;border-radius:15px; }");sb.AppendLine(".node { float:left;width:20px;height:20px;font-size:12px;line-height:20px;border:solid 1px #FF6701;background-color:#FAFAF0;text-align:center;border-radius:10px; }");sb.AppendLine(".arrow { float:left;width:20px;height:20px;font-size:12px;line-height:20px;border:solid 0px #FF6701;background-color:#FFFFFF;text-align:center; }");sb.AppendLine("</style>");sb.AppendLine("<script type=\"text/javascript\" src=\"" + Application.StartupPath.Replace(@"\", @"/") + "/jquery-3.6.0.min.js\"></script>");sb.AppendLine("<script type=\"text/javascript\" src=\"" + Application.StartupPath.Replace(@"\", @"/") + "/dfsbfs.js\"></script>");sb.AppendLine("</head>");sb.AppendLine("<body>");sb.AppendLine("<img src='https://img-blog.csdn.net/20180609184540410' width='400'><br>");sb.AppendLine(ShowInTable());sb.AppendLine("<br>");int k = 0;foreach (NodeInfo node in PathResult){sb.AppendLine("<div class='node'>" + node.Id + "</div>");sb.AppendLine("<div class='arrow'>→</div>");if (k >= loop) break;k++;}sb.AppendLine("<script language=\"javascript\">");sb.AppendLine("$(document).ready(function() {");sb.AppendLine("CanvasCreate();");foreach(NodeInfo node in TreeTotal.Nodes){for (int i = 0; i < node.Neighbors.Length; i++){sb.AppendLine("Connect(\"" + node.Id + "\", \""+ node.Neighbors[i] + "\");");}}sb.AppendLine("});");sb.AppendLine("</script>");sb.AppendLine("</body>");sb.AppendLine("</html>");return sb.ToString();}int loop = 0;private void button1_Click(object sender, EventArgs e){TreeTotal = TreeGrowth();PathResult = DFS(TreeTotal, TreeTotal.First());timer1.Interval = 1000;timer1.Enabled = true;loop = 0;}private void button2_Click(object sender, EventArgs e){TreeTotal = TreeGrowth();PathResult = BFS(TreeTotal, TreeTotal.First());timer1.Interval = 1000;timer1.Enabled = true;loop = 0;}public string ShowInTable(){int[,] matrix = new int[4, 9]{{ 0,0,0,0,1,0,0,0,0 },{ 0,3,0,0,2,0,0,4,0 },{ 7,9,100,5,8,300,6,10,200 },{ 0,400,0,0,0,0,0,0,0 },};for(int i = 0; i < TreeTotal.Nodes.Count; i++){TreeTotal.Nodes[i].Visited = false;}for (int i = 0; i <= loop; i++){PathResult[i].Visited = true;}StringBuilder sb = new StringBuilder();sb.AppendLine("<style>td { padding:10px; }</style>");sb.AppendLine("<table width='300' border='1' bordercolor='#EEEEEE' style='border-collapse:collapse;'>");for (int y = 0; y < 4; y++){sb.AppendLine("<tr>");for (int x = 0; x < 9; x++){int nk = matrix[y, x];if (nk >= 100) nk = 10 + nk / 100;if (nk == 0){sb.Append("<td></td>");}else if (TreeTotal.Nodes[nk - 1].Visited == true){sb.Append("<td><div class='ball2'>" + TreeTotal.Nodes[nk - 1].Id + "</div></td>");}else{sb.Append("<td><div class='ball1'>" + TreeTotal.Nodes[nk - 1].Id + "</div></td>");}}sb.AppendLine("</tr>");}sb.AppendLine("</table>");return sb.ToString();}private void timer1_Tick(object sender, EventArgs e){if (loop < PathResult.Count){webBrowser1.DocumentText = ShowPath();loop++;return;}loop = 0;}}/// <summary>/// 树/// </summary>public class TreeInfo{/// <summary>/// 所有节点/// </summary>public List<NodeInfo> Nodes { get; set; } = new List<NodeInfo>();/// <summary>/// 新增节点/// </summary>/// <param name="node"></param>public void Append(NodeInfo node){Nodes.Add(node);}/// <summary>/// 第一个节点/// </summary>/// <returns></returns>public NodeInfo First(){return Nodes[0];}/// <summary>/// 搜索指定节点的邻居（邻接节点）/// </summary>/// <param name="node"></param>/// <returns></returns>public List<NodeInfo> FindNeighbors(NodeInfo node){List<NodeInfo> list = new List<NodeInfo>();foreach (int nx in node.Neighbors){list.Add(Nodes.FirstOrDefault(k => k.Id == nx));}return list;}}/// <summary>/// 节点信息/// 来自：https://blog.csdn.net/CSDNBigBoy/article/details/80635220/// </summary>public class NodeInfo{/// <summary>/// 节点的id/// </summary>public int Id { get; set; } = 0;/// <summary>/// 是否被遍历过的标记，默认false表示没有被遍历过/// </summary>public bool Visited { get; set; } = false;/// <summary>/// 用于存储该元素的临接元素的id/// </summary>public int[] Neighbors { get; set; } = null;/// <summary>/// 构造函数/// </summary>public NodeInfo() { }/// <summary>/// 构造函数/// </summary>/// <param name="id"></param>/// <param name="neighbors"></param>public NodeInfo(int id, int[] neighbors){Id = id;Neighbors = neighbors;}}
}

有动图，效果就是不一样！

需要两个 js 文件，一个是 jQuery ，自己去下载吧。

另外一个画（绘制）树结构的源代码 dfsbfs.js。

在工程包内，下载解压即可。

——————————————————————

POWER BY 315SOFT.COM &
TRUFFER.CN