贝塞尔曲线（Bézier curve）是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是用来做这种矢量曲线的。

贝塞尔曲线由四个点（起始点、终止点以及两个相互分离的中间点）定义。滑动两个中间点，贝塞尔曲线的形状会发生变化。其可以通过三个点来确定一条平滑的曲线，而其有趣之处更在于它的“皮筋效应”，也就是说，随着点有规律地移动，曲线将产生皮筋伸引一样的变换，带来视觉上的冲击。

在历史上，研究贝塞尔曲线的人最初是按照已知曲线参数方程来确定四个点的思路设计出这种矢量曲线绘制法。 1962年，法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法，并给出了详细的计算公式，因此按照这样的公式绘制出来的曲线就用他的姓氏来命名，称为贝塞尔曲线。

贝塞尔曲线根据控制点的数量分为：

1、一阶贝塞尔曲线（2 个控制点）

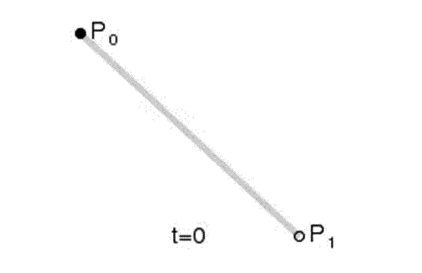
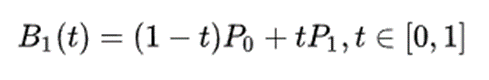
2、二阶贝塞尔曲线（3 个控制点）

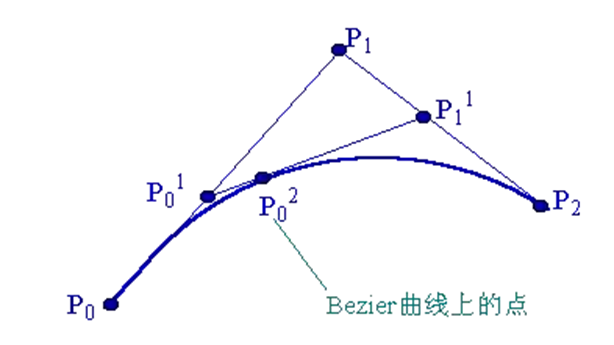
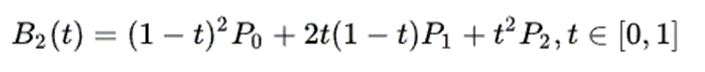
3、三阶贝塞尔曲线（4 个控制点）

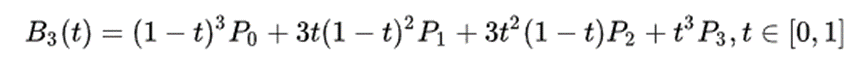
4、n阶贝塞尔曲线（n+1个控制点）

计算二阶贝塞尔曲线的例子：

#include <iostream>
#include <vector>
#include <cmath>
​
struct Point {double x, y;
};
​
Point bezierCurve(const std::vector<Point>& controlPoints, double t) {int n = controlPoints.size() - 1;std::vector<Point> tempPoints(n + 1);
​for (int i = 0; i <= n; ++i) {tempPoints[i].x = (1 - t) * (1 - t) * (1 - t) * controlPoints[i].x +3 * (1 - t) * (1 - t) * t * controlPoints[i + 1].x +3 * (1 - t) * t * t * controlPoints[i + 1].x +t * t * t * controlPoints[i + 1].x;tempPoints[i].y = (1 - t) * (1 - t) * (1 - t) * controlPoints[i].y +3 * (1 - t) * (1 - t) * t * controlPoints[i + 1].y +3 * (1 - t) * t * t * controlPoints[i + 1].y +t * t * t * controlPoints[i + 1].y;}
​return tempPoints[0];
}
​
int main() {std::vector<Point> controlPoints = {{0, 0}, {0.5, 1}, {1, 0}};double step = 0.01;
​for (double t = 0; t <= 1; t += step) {Point pointOnCurve = bezierCurve(controlPoints, t);std::cout << "t: " << t << ", x: " << pointOnCurve.x << ", y: " << pointOnCurve.y << std::endl;}system("pause");return 0;
}
​