121.买卖股票的最佳时机
初始思路:
暴力解法,两个for循环。
class Solution {public int maxProfit(int[] prices) {int res = Integer.MIN_VALUE;for(int i = 0;i<prices.length;i++){for(int j = i+1;j<prices.length;j++){res = Math.max(res,prices[j]-prices[i]);}}return res<0?0:res;}
}会超出时间限制。
题解复盘:
好吧想不出来dp数组该怎么定义。
动态规划五部曲:
1)确定dp数组(dp table)以及下标的含义:
dp[i][0]表示第i天持有股票所得最多现金
dp[i][1]表示第i天不持有股票所得最多现金
2)确定递推公式:
如果第i天持有股票即dp[i][0],可以是第i天买了股票也可以是第i天没买但第i-天就持有股票。
dp[i][0] = max(dp[i - 1][0], -prices[i]);
如果第i天不持有股票即dp[i][1],可能是我第i天卖出了,也可能是我第i-1天就不持有。
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
3)初始化:
dp[0][0] -= prices[0];
dp[0][1] = 0;
4)遍历顺序:
从前往后
5)举例推导
以示例1,输入:[7,1,5,3,6,4]为例,dp数组状态如下:
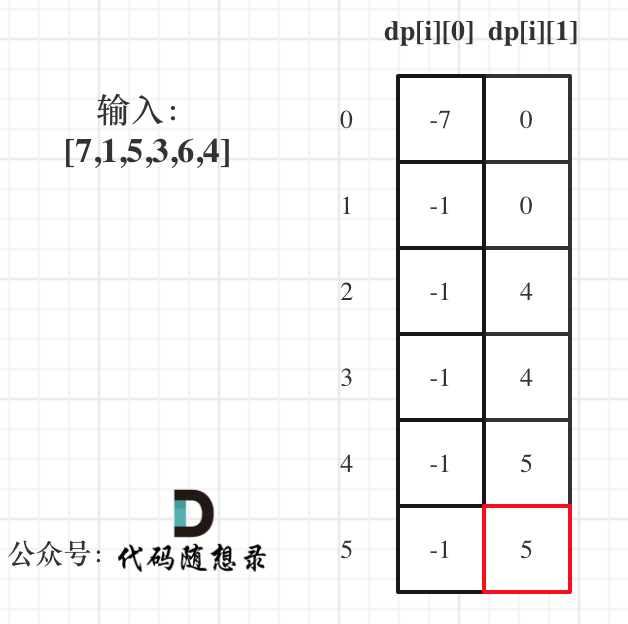
dp[5][1]就是最终结果。
为什么不是dp[5][0]呢?
因为本题中不持有股票状态所得金钱一定比持有股票状态得到的多!
class Solution {public int maxProfit(int[] prices) {int[][]dp = new int[prices.length][2];dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1;i<prices.length;i++){dp[i][0] = Math.max(dp[i-1][0],-prices[i]);dp[i][1] = Math.max(dp[i-1][0]+prices[i],dp[i-1][1]);}return dp[prices.length-1][1];}
}这里我纳闷了一下为什么 dp[i][0] = Math.max(dp[i-1][0],-prices[i]);而不是
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
主要是因为本题只可以买一次,所以第一次购入的时候的现金一定是- prices[i], dp[i - 1][1] - prices[i]也就涉及了多次买卖。
122.买卖股票的最佳时机II
由上面的结果修改一下直接得到第二道题目的答案。
class Solution {public int maxProfit(int[] prices) {int[][] dp = new int[prices.length][2];dp[0][0] = -prices[0];dp[0][1] = 0;for (int i = 1; i < prices.length; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);System.out.println(dp[i][0]);dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);System.out.println(dp[i][1]);}return dp[prices.length - 1][1];}
}123.买卖股票的最佳时机III
相比于上一题不限制次数的交易,本题的重点在于我最多只能交易两次。
初始思路&&题解复盘
- 确定dp数组以及下标的含义
一天一共就有五个状态,
- 没有操作 (其实我们也可以不设置这个状态)
- 第一次持有股票
- 第一次不持有股票
- 第二次持有股票
- 第二次不持有股票
dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天状态j所剩最大现金。
2.确定递推公式
达到dp[i][1]状态,有两个具体操作:
- 操作一:第i天买入股票了,那么dp[i][1] = dp[i-1][0] - prices[i]
- 操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][1] = dp[i - 1][1]
那么dp[i][1]究竟选 dp[i-1][0] - prices[i],还是dp[i - 1][1]呢?
一定是选最大的,所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
同理dp[i][2]也有两个操作:
- 操作一:第i天卖出股票了,那么dp[i][2] = dp[i - 1][1] + prices[i]
- 操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
同理可推出剩下状态部分:
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
3.dp数组如何初始化
第0天没有操作,这个最容易想到,就是0,即:dp[0][0] = 0;
第0天做第一次买入的操作,dp[0][1] = -prices[0];
第0天做第一次卖出的操作,这个初始值应该是多少呢?
此时还没有买入,怎么就卖出呢? 其实大家可以理解当天买入,当天卖出,所以dp[0][2] = 0;
第0天第二次买入操作,初始值应该是多少呢?应该不少同学疑惑,第一次还没买入呢,怎么初始化第二次买入呢?
第二次买入依赖于第一次卖出的状态,其实相当于第0天第一次买入了,第一次卖出了,然后再买入一次(第二次买入),那么现在手头上没有现金,只要买入,现金就做相应的减少。
所以第二次买入操作,初始化为:dp[0][3] = -prices[0];
同理第二次卖出初始化dp[0][4] = 0;
class Solution {public int maxProfit(int[] prices) {int[][] dp = new int[prices.length][5];int res = Integer.MIN_VALUE;dp[0][0] = 0;dp[0][1] = -prices[0];dp[0][3] = -prices[0];for(int i = 1;i<prices.length;i++){dp[i][0] = dp[i-1][0];dp[i][1] = Math.max(dp[i-1][0]-prices[i],dp[i-1][1]);dp[i][2] = Math.max(dp[i-1][1]+prices[i],dp[i-1][2]);dp[i][3] = Math.max(dp[i-1][2]-prices[i],dp[i-1][3]);dp[i][4] = Math.max(dp[i-1][3]+prices[i],dp[i-1][4]);}for(int i = 0;i<5;i++){res = Math.max(res, dp[prices.length-1][i]);}return res;}
}
第一次解答的时候第2次买入的时候初始化为0导致计算错误,接下来书写的时候需要注意,只要买入就是-prices[0];
188.买卖股票的最佳时机IV
初始思路&&题解复盘:
在上一题目的基础之上,总结了规律的感觉。
class Solution {public int maxProfit(int k, int[] prices) {//买卖k次的话是2k+1种情况;int[][] dp = new int[prices.length][2*k+1];for(int i = 1;i<2*k+1;i = i+2){dp[0][i] = -prices[0];}for(int i = 1;i<prices.length;i++){for(int j= 1;j<2*k+1;j++){if(j%2!=0){dp[i][j] = Math.max(dp[i-1][j-1]-prices[i],dp[i-1][j]);}else{dp[i][j] = Math.max(dp[i-1][j-1]+prices[i],dp[i-1][j]); }}}return dp[prices.length-1][2*k];}
}class Solution {public int maxProfit(int k, int[] prices) {if (prices.length == 0) return 0;// [天数][股票状态]// 股票状态: 奇数表示第 k 次交易持有/买入, 偶数表示第 k 次交易不持有/卖出, 0 表示没有操作int len = prices.length;int[][] dp = new int[len][k*2 + 1];// dp数组的初始化, 与版本一同理for (int i = 1; i < k*2; i += 2) {dp[0][i] = -prices[0];}for (int i = 1; i < len; i++) {for (int j = 0; j < k*2 - 1; j += 2) {dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[len - 1][k*2];}
}题解计算量更小
309.买卖股票的最佳时机含冷冻期
初始思路:
由上面的题目可以发现这部分重点依旧在于分析状态,从而得到dp数组的定义和递推公式
在此我认为拥有三种状态,
当前未拥有股票,但不是当天卖出的,下一阶段可在此状态下购入;
当前未拥有股票,但是是当天卖出的,下一阶段不可在该状态下购入。
当前拥有股票,可能是上一阶段购入的,也可能是在第一状态下购入的。
class Solution {public int maxProfit(int[] prices) {if(prices.length==1){return 0;}int[][] dp = new int[prices.length][3];dp[0][1] = -prices[0];for(int i = 1;i<prices.length;i++){dp[i][0] = Math.max(dp[i-1][0],dp[i-1][2]);dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);dp[i][2] = dp[i-1][1]+prices[i];}return Math.max(dp[prices.length-1][0],dp[prices.length-1][2]);}
}题解复盘:
分为了四个状态,更加清晰:
具体可以区分出如下四个状态:
- 状态一:持有股票状态(今天买入股票,或者是之前就买入了股票然后没有操作,一直持有)
- 不持有股票状态,这里就有两种卖出股票状态
- 状态二:保持卖出股票的状态(两天前就卖出了股票,度过一天冷冻期。或者是前一天就是卖出股票状态,一直没操作)
- 状态三:今天卖出股票
- 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!

j的状态为:
- 0:状态一
- 1:状态二
- 2:状态三
- 3:状态四
注意这里的每一个状态,例如状态一,是持有股票股票状态并不是说今天一定就买入股票,而是说保持买入股票的状态即:可能是前几天买入的,之后一直没操作,所以保持买入股票的状态。
- 确定递推公式
达到买入股票状态(状态一)即:dp[i][0],有两个具体操作:
- 操作一:前一天就是持有股票状态(状态一),dp[i][0] = dp[i - 1][0]
- 操作二:今天买入了,有两种情况
- 前一天是冷冻期(状态四),dp[i - 1][3] - prices[i]
- 前一天是保持卖出股票的状态(状态二),dp[i - 1][1] - prices[i]
那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);
达到保持卖出股票状态(状态二)即:dp[i][1],有两个具体操作:
- 操作一:前一天就是状态二
- 操作二:前一天是冷冻期(状态四)
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
达到今天就卖出股票状态(状态三),即:dp[i][2] ,只有一个操作:
昨天一定是持有股票状态(状态一),今天卖出
即:dp[i][2] = dp[i - 1][0] + prices[i];
达到冷冻期状态(状态四),即:dp[i][3],只有一个操作:
昨天卖出了股票(状态三)
dp[i][3] = dp[i - 1][2];
综上分析,递推代码如下:
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];714.买卖股票的最佳时机含手续费
初始思路:
由上面的题目可以发现这部分重点依旧在于分析状态,从而得到dp数组的定义和递推公式。但其实就是在122的基础上增加了手续费。
class Solution {public int maxProfit(int[] prices, int fee) {int[][] dp = new int[prices.length][2];dp[0][0] = -prices[0];dp[0][1] = 0;for (int i = 1; i < prices.length; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = Math.max(dp[i - 1][0] + prices[i]-fee, dp[i - 1][1]);}return dp[prices.length - 1][1];}
}
![[C]jupyter中使用C](https://img-blog.csdnimg.cn/direct/ce73a10d5d9548e9bae8daddbf1fc68e.png)