存在重复元素Ⅲ
题目要求

解题思路
主要使用滑动窗口方法,让滑动窗口代销固定为t。
本题最大的难点在于快速地找到滑动窗口内的最大值和最小值,以及删除指定元素。
如果遍历求滑动窗口内的最大值和最小值,时间复杂度是O(K),肯定会超时。降低时间复杂度的一个绝招就是增加空间复杂度:利用更好的数据结构。是的,我们的目的就是快速让一组数据有序,那就寻找一个**内部是有序的数据结构呗!**下面分语言讲解一下常见的内部有序的数据结构。
- 在 C++ 中 set/multiset/map 内部元素是有序的,它们都要基于红黑树实现。其中 set 会对元素去重,而 multiset 可以有重复元素,map 是 key 有序的哈希表。
- 在 Java 中TreeSet 是有序的去重集合, TreeMap 是 key 有序的哈希表,它们也是基于红黑树实现的
- 在Python 中sortedcontainers 实现了有序的容器
下面这个图是 C++ 的multiset 内部结构示意图,它是个**平衡二叉搜索树(BST)**插入元素时会自动调整二叉树,使得每个子树根节点的键值大于左子树所有节点的键值,同时保证根节点的左右子树的高度相等。这样子的二叉树高度最小,检索速度最快。它的中序遍历是有序的,另外它也允许出现重复的值。
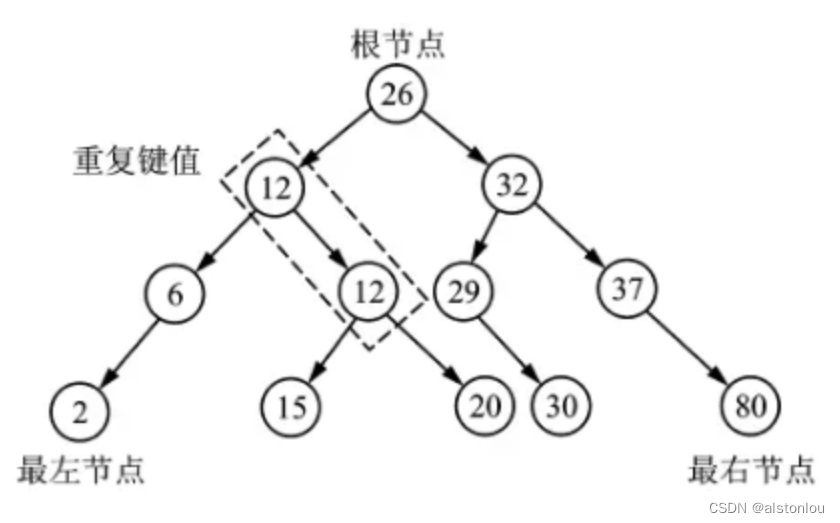
本题要点:
- 本题需要保存滑动窗口内的所有元素,可以使用 C++ 的multiset/map/set 与 Java 中的TreeMap
- 当频繁的插入和删除元素时,multiset/map 和TreeMap等有序的数据结构能够在O(log(K))的时间复杂度内调整BST,从而维护结构的有序性
- multiset和TreeMap 都能提供了获取第一个元素和最后一个元素的函数,也就能在O(1)的时间内获得滑动窗口内最小值和最大值。
代码
class Solution(object):def containsNearbyAlmostDuplicate(self, nums, k, t):from sortedcontainers import SortedSetst = SortedSet()left, right = 0, 0res = 0while right < len(nums):if right - left > k:st.remove(nums[left])left += 1index = bisect.bisect_left(st, nums[right] - t)if st and index >= 0 and index < len(st) and abs(st[index] - nums[right]) <= t:return Truest.add(nums[right])right += 1return False
复杂度分析
时间复杂度: O ( N ∗ l o g ( m i n ( n , k ) ) ) O(N * log (min(n,k))) O(N∗log(min(n,k))),每个元素遍历一次,新元素插入红黑树的调整时间为 O ( l o g ( x ) ) O(log(x)) O(log(x)),set中最多有min(n,k)个元素
空间复杂度: O ( m i n ( n , k ) ) O(min(n,k)) O(min(n,k))
其他解法
######### 桶排序的思想,借助一个个桶if t < 0: #abs不可能 < 0return Falsebucket_len = t + 1bucket = dict()for i, num in enumerate(nums):ID = num // bucket_len ## python3 向左取整if ID in bucket:return Trueif (ID-1) in bucket and abs(bucket[ID-1] - num) <= t:return Trueif (ID+1) in bucket and abs(bucket[ID+1] - num) <= t:return Truebucket[ID] = numif i >= k:#del bucket[ nums[i-k] // (t + 1)]bucket.pop( nums[i-k] // (t+1) )return False