【学习总结】地面路谱分析-编程知识

【学习总结】地面路谱分析

本文仅用于记录自己的学习总结，包括个人理解。不保证内容严格正确。

0. 参考资料

[1] 国标GB/T 703-2005/ISO 8608:1995。
[2] Bilibili-车辆考研-路面不平度统计特性
[3] Bilibili-清华大学《汽车理论》
[4] 网络参考文档.
[5] 论文：高雄《路面不平度统计特性的改进》，工程价值，2023。

网盘：https://pan.baidu.com/s/1ameuQwdOquCrk2V1PIS-Xw?pwd=ut9m

1. 路面空间功率谱密度 $G_q(n)$ 拟合公式

$G_q(n)=G_q(n_0)(\frac{n}{n_0})^{-W}$ 公式中符号的含义：
n：空间频率，单位 $m^{-1}$ ，表示“每米长度有几个波长”，对应常说的“时间频率”，及 $1/ s, Hz$
n0：参考空间频率，为固定值， $n_0=0.1 m^{-1}$
$G_q(n_0)$ ：参考空间频率下的路面功率谱密度，即“路面不平度系数”
W：频率指数，一般取 2。没什么原因，就是一般取2。

关于式子的理解：

关于 $G_q(x)$ ：是 $x$ 频率对应的功率密度，即某个频率对应的能量。
$n_0$ ：我们选择了一个特定的(空间)频率，即 $n_0=0.1 m^{-1}$ （注意单位不是Hz，因为 $Hz = 1/ s$ ），即波长 $\lambda=10m$ 。
$G_q(n_0)$ ：对于选定的这个 $n_0$ ，计算得到的功率密度，就是 $G_q(n_0)$ ；

那么其他不同频率，对应的功率密度是多少呢？也就是说，当频率取 $n$ 时，功率密度的值 $G_q(n)$ 是多少呢？
可以直接计算。也可以通过上面的那个式子进行拟合，即经过了许多人做了的大量的实验，统计表明，任意频率 $n$ 的值，可以用参考值 $n_0$ 对应的 $G_q(n_0)$ ，进行拟合。拟合时一般拟合出来的 $W$ 取值都在2左右，因此说上述式子的 $W$ 取2。

讨论：拟合的是否合适呢？

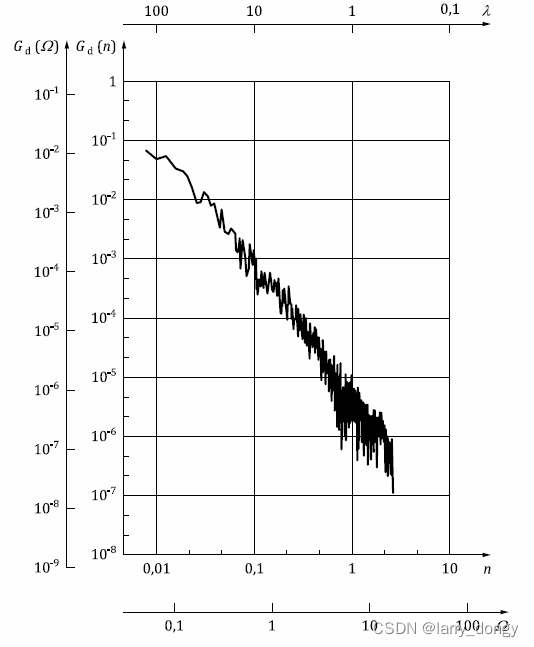
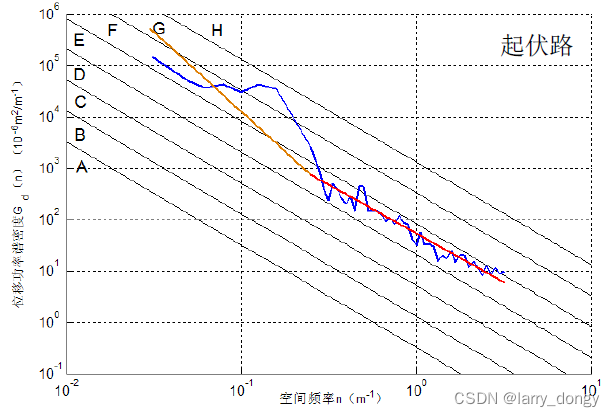
下图来自ISO标准中的图片，横轴是频率，纵轴是功率密度，合起来就是“谱线”，即“功率谱密度”。
可以看出，n从0.01到0.1时， $G_d$ *（图片中的d表示distance，和上面用的q是一个含义）下降了2个大格子（从10的-1降到了-3），
所以斜率大概是 $- 2$ ，也就是上面的 $W$ 取值是-2是合适的。
在这里插入图片描述

2. 道路分级

$G_q(n_0)$ 的值有什么意义？如果说，上面拟合曲线时，固定了 $W$ ，此时曲线的特性（上下平移量）只与 $G_q(n_0)$ 有关，那么可以根据 $G_q(n_0)$ 的数值，对路面进行分级。根据 $G_q(n_0)$ 的取值，分级依据如下：
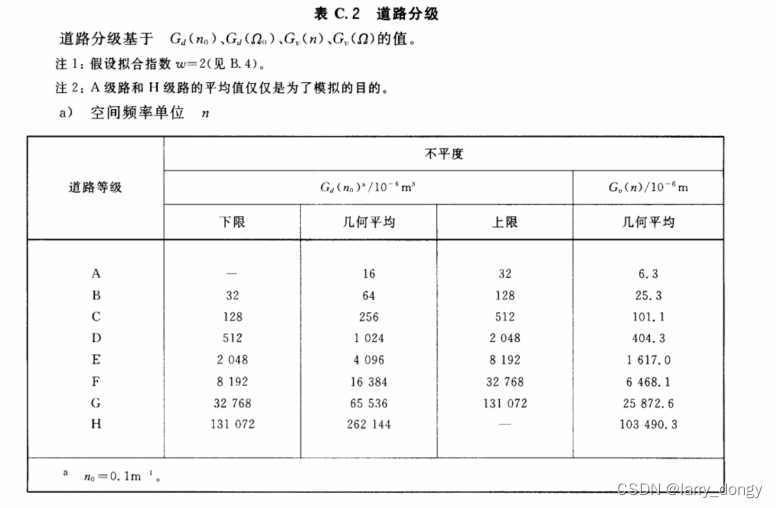
《GBT7031-2005》的表C.2
可以看出，A级路面标准很高，在10m长度（ $n_0$ 取0.1 $m^{-1}$ ）时，数值在 $16e^{-6}$ 左右，在mm以下了。

表中，几何平均是如何计算的？
由参考资料[5]，可以计算出结果。

3. 速度/加速度功率谱密度

速度功率谱密度： $G_v(n)=(2\pi n)^2 G_q(n)$
加速度功率谱密度： $G_a(n)=(2\pi n)^4 G_q(n)$

当 $W = 2$ 时，速度的表达式为： $G_v(n)=(2\pi n)^2 G_q(n_0)$ ，此时与 $n$ 无关了。很独特的情况。

4. 时间频率功率谱密度 $G_q(f)$

上述的谱密度是空间的，没有考虑车速。如果考虑到车速，应该有入如下表达式：
$f = v n$ ，即 “时间频率=车速*空间频率”，对应量纲 $Hz=m/s *m^{-1}$ 也是合理的。

此时，可以得到位移/速度/加速度的时间频率功率谱密度分别为：
位移： $G_q(f)=\frac{1}{v}G_q(n_0)(\frac{n}{n_0})^2=G_q(n_0)n_0^2 \frac{v}{f^2}$
速度： $G_v(f)=4\pi^2 G_q(n_0)n_0^2 v$
加速度： $G_a(f)=16\pi^4 G_q(n_0)n_0^2 v f^2$
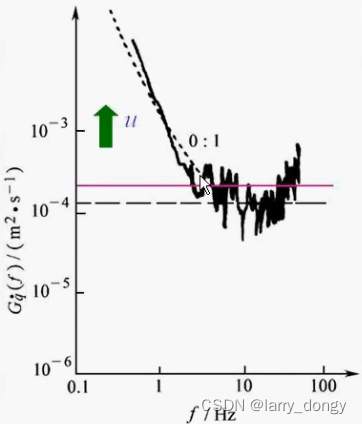
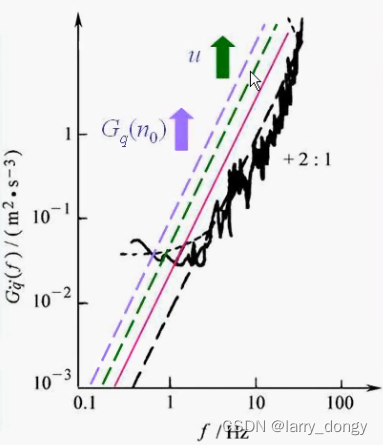
可以看出，速度的和 $f$ 无关。