【Python机器学习】SVM——线性模型与非线性特征-编程知识

【Python机器学习】SVM——线性模型与非线性特征

SVM（核支持向量机）是一种监督学习模型，是可以推广到更复杂模型的扩展，这些模型无法被输入空间的超平面定义。

线模型在低维空间中可能非常受限，因为线和平面的灵活性有限，但是有一种方式可以让线性模型更加灵活，那就是添加更多特征，比如输入特征的交互式或多项式。

以下面的数据集为例：

from sklearn.datasets import make_blobs
import mglearn
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVCplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X,y=make_blobs(centers=4,random_state=8)
y=y%2
line_svc=LinearSVC().fit(X,y)mglearn.plots.plot_2d_separator(line_svc,X)
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel('特征0')
plt.ylabel('特征1')
plt.show()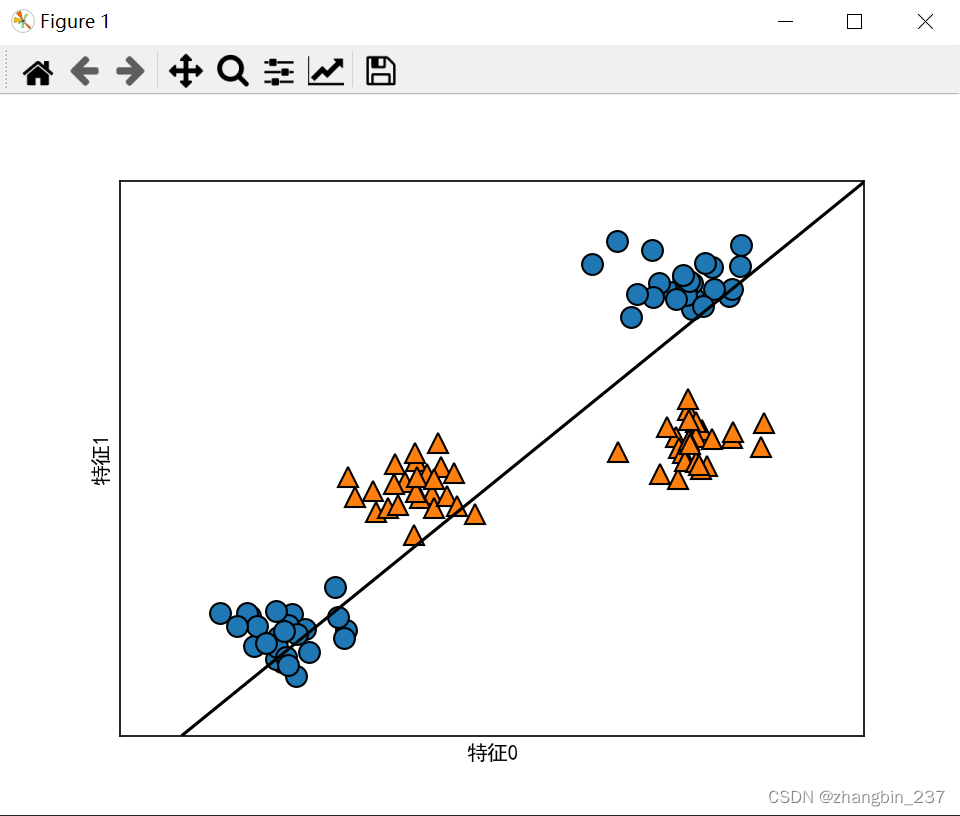

用于分类的线性模型只能用一条直线来划分数据点，对这个数据集无法给出较好的结果。

现在，对输入特征进行扩展，比如添加一个特征的平方作为一个新特征，那么每个数据点可以表示为三维点，而不是二维点，这样就可以做一个新的三维散点图：

import numpy as np
from sklearn.datasets import make_blobs
import mglearn
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
from mpl_toolkits.mplot3d import Axes3D,axes3dplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X,y=make_blobs(centers=4,random_state=8)
y=y%2
#line_svc=LinearSVC().fit(X,y)
X_new=np.hstack([X,X[:,1:]**2])
figure=plt.figure()#3D可视化
ax=figure.add_subplot(projection='3d')
#首先画出所有y==0，然后画出所有y==1的点
mask=y==0ax.scatter(X_new[mask,0],X_new[mask,1],X_new[mask,2],c='blue',marker='o',cmap=mglearn.cm2,s=60)
ax.scatter(X_new[~mask,0],X_new[~mask,1],X_new[~mask,2],c='red',marker='^',cmap=mglearn.cm2,s=60)
ax.set_xlabel('特征0')
ax.set_ylabel('特征1')
ax.set_zlabel('特征1**2')
plt.show()

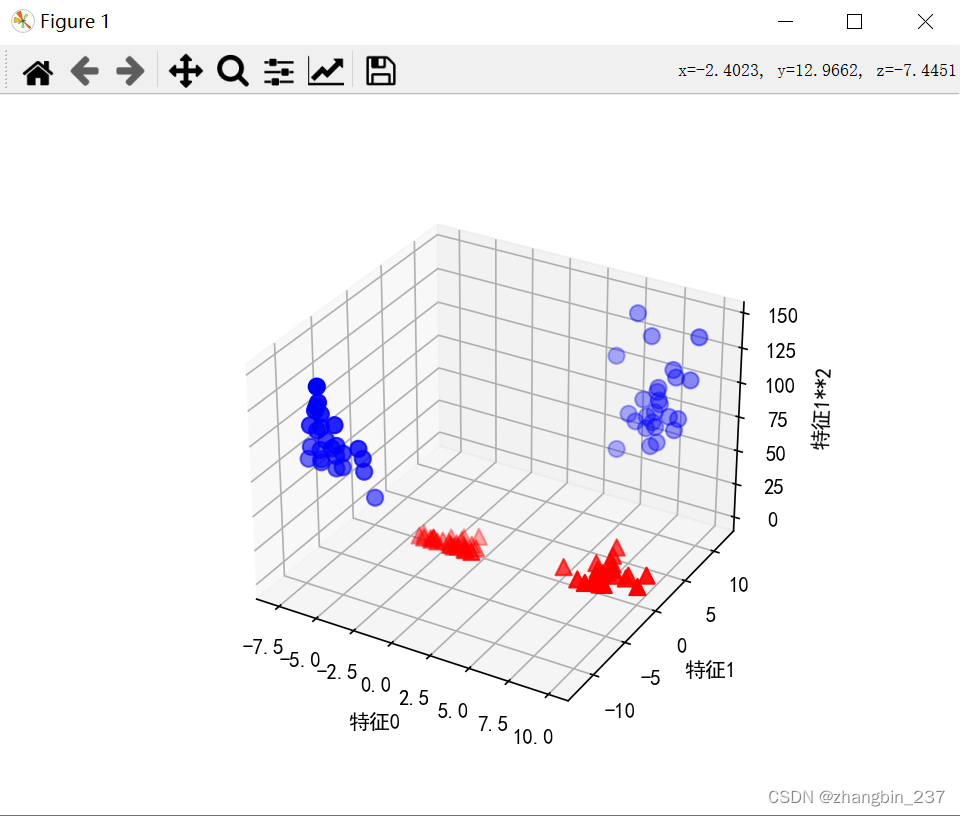
在数据新的可视化中，可以用线性模型（三维平面将这两个类别区分开）

import numpy as np
from sklearn.datasets import make_blobs
import mglearn
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
from mpl_toolkits.mplot3d import Axes3D,axes3dplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X,y=make_blobs(centers=4,random_state=8)
y=y%2
X_new=np.hstack([X,X[:,1:]**2])
line_svc_3d=LinearSVC().fit(X_new,y)
coef,intercept=line_svc_3d.coef_.ravel(),line_svc_3d.intercept_figure=plt.figure()#3D可视化
ax=figure.add_subplot(projection='3d')
#首先画出所有y==0，然后画出所有y==1的点
xx=np.linspace(X_new[:,0].min()-2,X_new[:,0].max()+2,50)
yy=np.linspace(X_new[:,1].min()-2,X_new[:,1].max()+2,50)
XX,YY=np.meshgrid(xx,yy)
ZZ=(coef[0]*XX+coef[1]*YY+intercept)/-coef[2]
mask=y==0
ax.plot_surface(XX,YY,ZZ,rstride=8,cstride=8,alpha=0.3)
ax.scatter(X_new[mask,0],X_new[mask,1],X_new[mask,2],c='blue',marker='o',cmap=mglearn.cm2,s=60)
ax.scatter(X_new[~mask,0],X_new[~mask,1],X_new[~mask,2],c='red',marker='^',cmap=mglearn.cm2,s=60)
ax.set_xlabel('特征0')
ax.set_ylabel('特征1')
ax.set_zlabel('特征1**2')
plt.show()

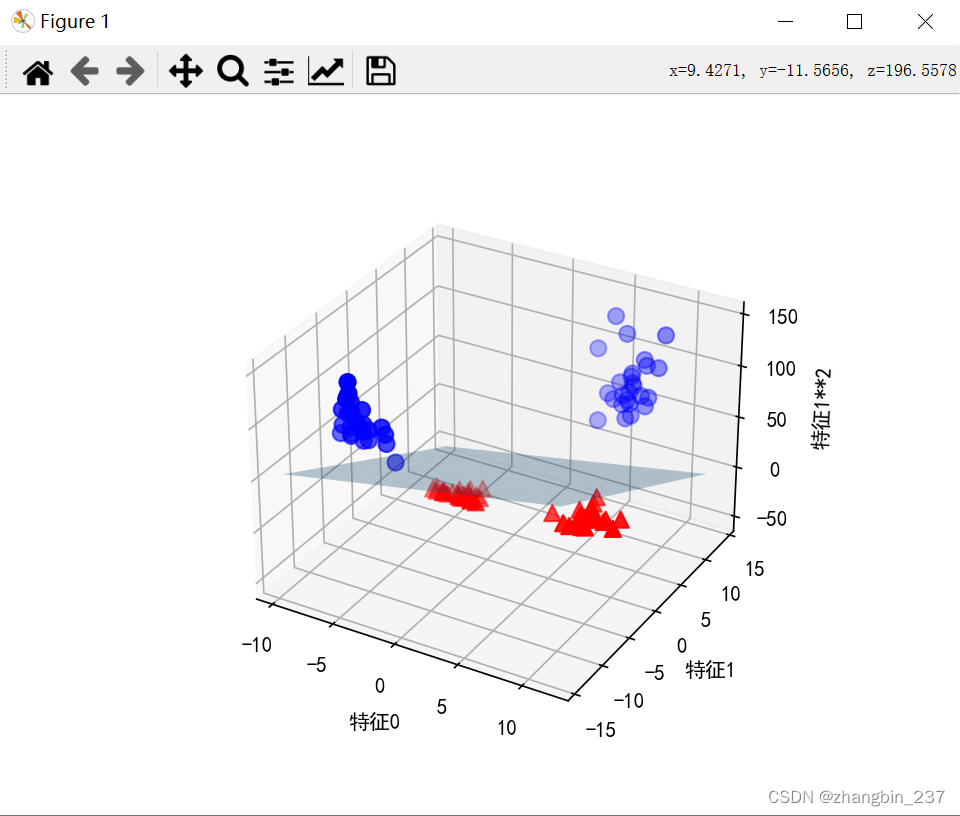
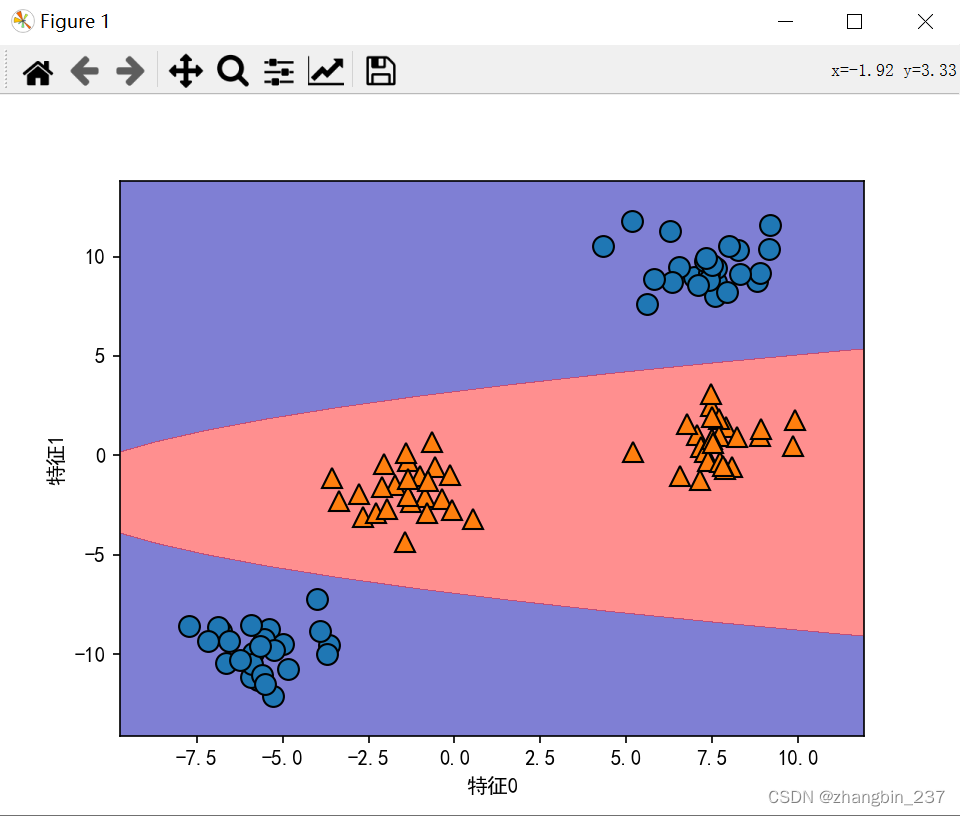
如果将线性SVM模型看做原始特征的函数，那么它实际上已经不是线性的了，它不再是一条直线，而是一个椭圆：

import numpy as np
from sklearn.datasets import make_blobs
import mglearn
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
from mpl_toolkits.mplot3d import Axes3D,axes3dplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X,y=make_blobs(centers=4,random_state=8)
y=y%2
X_new=np.hstack([X,X[:,1:]**2])
line_svc_3d=LinearSVC().fit(X_new,y)
coef,intercept=line_svc_3d.coef_.ravel(),line_svc_3d.intercept_
xx=np.linspace(X_new[:,0].min()-2,X_new[:,0].max()+2,50)
yy=np.linspace(X_new[:,1].min()-2,X_new[:,1].max()+2,50)
XX,YY=np.meshgrid(xx,yy)
ZZ=YY**2dec=line_svc_3d.decision_function(np.c_[XX.ravel(),YY.ravel(),ZZ.ravel()])
plt.contourf(XX,YY,dec.reshape(XX.shape),levels=[dec.min(),0,dec.max()],cmap=mglearn.cm2,alpha=0.5)
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel('特征0')
plt.ylabel('特征1')
plt.show()