343. 整数拆分(第二次做还是没弄明白)

力扣题目链接(opens new window)

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

• 输入: 2
• 输出: 1
• 解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

• 输入: 10
• 输出: 36
• 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

看到题目的第一想法

        dp ，列出最大乘积找规律，发现，按照3来拆分是能达到最大乘积的

        dp[i] 代表最大的乘积

        根据规律进行初始化，将dp[i-3] 与3 相乘

        但我的做法不太符合dp的规律

看到代码随想录之后的想法

        拆分成近似的数时，得到的乘积是最大的

        动规五部曲，很快的写出解题思路

        1确定dp数组以及对应下标的含义

        dp[i] 代表最大的乘积

        2确定递推公式

        dp[i][j] = dp[i-1][j]+dp[i][j-1]

        3dp数组初始化

        需要把第一行和第一列都初始化，都为1

        4确定遍历顺序

        从上往下，从前往后

        5手动推导dp数组

        6打印dp数组

        打印dp[m-1][n-1]

自己实现过程中遇到的困难

        注意初始化

class Solution {/*public int integerBreak(int n) {//确定dp和每个下标的含义//dp的每个下标对应每一个数的最大乘积？//确定递推公式//5开始，然后3加上对应下标的最大乘积//确定dp数组的初始条件//dp[0]=1 dp[1]=1 dp[2]=2 //确定遍历顺序//从前往后//举例推导dp数组//dp[0]=1 dp[1]=1 dp[2]=2 dp[3]=2 dp[4] =4 dp[5]=6 dp[6]=9 dp[7] = 3*dp[7-3] dp[8]=3+dp[8-3] //打印dp数组if(n==2){return 1;}if(n==3){return 2;}if(n==4){return 4;}if(n==5){return 6;}if(n==6){return 9;}int dp[] = new int[n];dp[1]=1;dp[2]=2;dp[3]=4;dp[4]=6;dp[5]=9;for(int i=6;i<n;i++){dp[i]=3*dp[i-3];}return dp[n-1];}*///卡哥做法//我的做法的问题，dp的初始值设置的过多，违背的dp的本来含义，有点类似于拆成很多个3的感觉//卡哥做法:拆分当前值，存到dp数组中，dp[i] = max(i*(i-j),i*dp[i-j],dp[i]);// j*(i-j) 就是当前数拆成两个// j*dp[i-j] 就是当前数，和之前dp得到的最大数相乘的最大值，dp[i-j]存放的是拆分i-j所得到的最大值// dp[i] 记录就是得到的值动态变化，变化中的最大值就是dp[i] public int integerBreak(int n) {//确定dp和每个下标的含义//dp的每个下标对应每一个数的最大乘积？//确定递推公式//dp[i] = max(dp[i],j*(i-j),dp[i-j]*j)//确定dp数组的初始条件//dp[0]=0 dp[1]=0 dp[2]=1 //确定遍历顺序//从前往后//举例推导dp数组//dp[0]=0 dp[1]=0 dp[2] = 1//打印dp数组if(n==0){return 0;}if(n==1){return 0;}if(n==2){return 1;}int dp[] = new int[n+1];dp[0]=0;dp[1]=0;dp[2]=1;//注意是每个下标对应目标的值for(int i=3;i<=n;i++){//因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。//m一定>=2所以只要拆到i/2就行了 ，再往后拆一定不是最大值 for(int j=1;j<=i/2;j++){dp[i] = Math.max(dp[i],Math.max(j*(i-j),dp[i-j]*j));}}return dp[n];}
}

96. 不同的二叉搜索树

(总结时还是不太会)

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

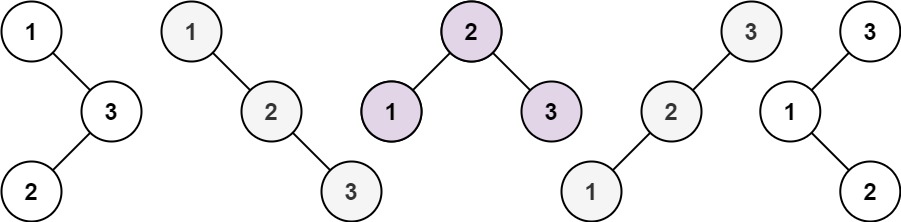
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

看到题目的第一想法

        dp ，记录种数

        但是没找到规律

看到代码随想录之后的想法

        动规五部曲，很快的写出解题思路

        1确定dp数组以及对应下标的含义

        dp[i] 代表不同的种数

        2确定递推公式

        左子树为0 右子树为n-1 dp[0]*dp[n-1]

        左子树为1 右子树为n-2  dp[1]*dp[n-2]

         左子树为2 右子树为n-3  dp[2]*dp[n-3]

         左子树为3 右子树为n-4   dp[3]*dp[n-4]

        。。。

        左子树为n-1 右子树为0 dp[n-1]*dp[0]

        第n棵树的种数就是把上述的都加起来

        dp[n]=dp[n-1]*dp[0]+dp[n-2]*dp[1]

        for循环0~i 累加起来

        
                //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                dp[i]+=dp[j-1]*dp[i-j];

        3dp数组初始化

        dp[0]=1

        4确定遍历顺序

        从前往后

        5手动推导dp数组

        6打印dp数组

        打印dp[m-1][n-1]

自己实现过程中遇到的困难

        注意初始化

        注意是双重for循环 外层0~n 里层0~i

        将根节点编号比较好理解  当根节点为第j个节点时，左边为j-1 右边为 i-jdp[j-1]*dp[i-j]

class Solution {//我没想到思路，卡哥给的思路是和正数拆分差不多，也是分为i j 来拆//第i棵二叉树的种数为 // 左边为i-1*右边为0 dp[i-1]*dp[0]// 左边为i-2*右边为1 dp[i-2]*dp[1]// 左边为i-3*右边为2 dp[i-3]*dp[2]// ... 把以上的相加public int numTrees(int n) {//确定dp数组以及每个下标的含义//当前二叉搜索树的种数//确定递推公式//dp[i]=dp[i-1]*dp[0]+dp[i-2]*dp[1]+dp[i-3]*dp[2]...//dp[i] = for(从j=0开始到i-1dp所记录的相乘)//dp数组的初始化//空树为0//dp[0]=1 dp[1]=1//确定遍历顺序//从前往后//举例推导dp数组//dp[0]=0 dp[1] = dp[0]*dp[0] =1 dp[2] = dp[1]*dp[0]+dp[0]*dp[1]=2int[] dp = new int[n+1];dp[0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){//如果dp[1]=dp[0]*dp[0]//这里是dp[j-1]*dp[i-j]// 举例 若i为4// 0 3 j=1// 1 2 j=2// 2 1 j=3// 3 0 j=4//对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加//一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-jdp[i]+=dp[j-1]*dp[i-j];}}return dp[n];}
}