1.合并二叉树(617题)
题目要求:
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
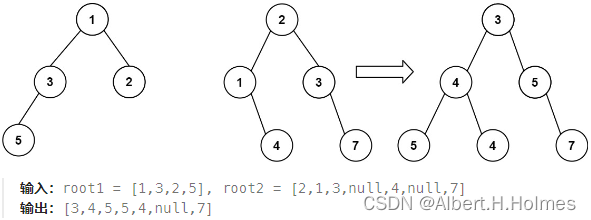
思路:遍历一个树逻辑是一样的,只不过传入两个树的节点,同时操作
递归法:参数是两个节点,这个是前序遍历,在1的树上进行修改
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1 == NULL)return root2;//如果1空了,就是2if(root2 == NULL)return root1;//如果2空了,就是1root1->val += root2->val;//在1的树上进行修改,两个树节点加起来root1->left = mergeTrees(root1->left,root2->left);//左root1->right = mergeTrees(root1->right,root2->right);//右return root1;}
};迭代法:层序遍历,迭代法中,一般一起操作两个树都是使用队列模拟类似层序遍历,同时处理两个树的节点
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1 == NULL)return root2;//1为空返回2if(root2 == NULL)return root1;//2为空返回1queue<TreeNode*>que;//队列que.push(root1);//将1和2压入队列中que.push(root2);while(!que.empty()){TreeNode* node1 = que.front();//节点1队头元素,再弹出que.pop();TreeNode* node2 = que.front();//节点2队头元素,弹出que.pop();//node1->val += node2->val;//将两个值相加然后给1的值//节点1和节点2的左节点不为空,压入队列if(node1->left != NULL && node2->left != NULL){que.push(node1->left);que.push(node2->left);}//节点1和节点2的右节点不为空,压入队列if(node1->right != NULL && node2->right != NULL){que.push(node1->right);que.push(node2->right);}//节点1的左节点为空,节点2的左节点不为空,节点2赋值给1if(node1->left == NULL && node2->left != NULL){node1->left = node2->left;}//节点1的右节点为空,节点2的右节点不为空,节点2赋值给1if(node1->right == NULL && node2->right != NULL){node1->right = node2->right;}}return root1;}
};2.二叉搜索树中的搜索(700题)
题目描述:给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
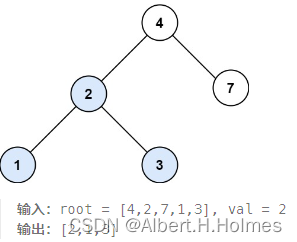
递归法:因为是二叉搜索树,知道树的特性,左边子树的节点小于中间节点,右边子树的节点大于中间节点
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if(root == NULL || root->val == val)return root;//根节点为空或者根节点的值等于目标值返回根节点TreeNode* result = NULL;//结果if(root->val > val)result = searchBST(root->left,val);//因为二叉搜索树,左边的节点小于根节点,相当于左遍历if(root->val < val)result = searchBST(root->right,val);//右边节点的值大于根节点的值,相当于右遍历return result;}
};迭代法:普通二叉树用栈或者队列做迭代,但是二叉搜索树特性节点有序,不用辅助也可以写迭代
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {//循环条件while(root != NULL){if(root->val > val)root = root->left;//根节点的值大于目标值,向左else if(root->val < val)root = root->right;//根节点的值小于目标值,向右else return root;//相等返回根节点}return NULL;//不等返回空}
};要记住二叉搜索树的特性,节点有序
3.验证二叉搜索树(98题)
题目描述:
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
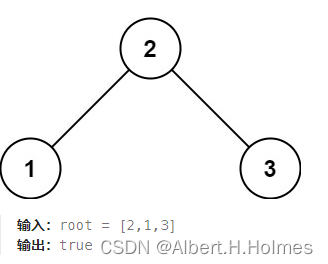
递归法: 1.数组方法
class Solution {
private://中序遍历,把用数组接收,最后看数组是否升序即可vector<int>vec;void traversal(TreeNode* root){if(root == NULL)return ;//终止条件traversal(root->left);//左vec.push_back(root->val);//中traversal(root->right);//右}
public:bool isValidBST(TreeNode* root) {vec.clear();traversal(root);//递归函数//遍历数组,然后判断是否数组升序for(int i = 1;i < vec.size();i++){if(vec[i] <= vec[i-1])return false;//逻辑}return true;}
};2.节点方法:相当于数组的双指针,pre记录前一个节点走过遍历
class Solution {
public:TreeNode* pre = NULL; // 用来记录前一个节点bool isValidBST(TreeNode* root) {if (root == NULL) return true;bool left = isValidBST(root->left);if (pre != NULL && pre->val >= root->val) return false;pre = root; // 记录前一个节点bool right = isValidBST(root->right);return left && right;}
};迭代法:中序遍历
class Solution {
public:bool isValidBST(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;TreeNode* pre = NULL;//记录前一个节点while (cur != NULL || !st.empty()) {if (cur != NULL) {st.push(cur);cur = cur->left;//左} else {cur = st.top();//中st.pop();if (pre != NULL && cur->val <= pre->val) return false;pre = cur;cur = cur->right;//右}}return true;}
};4.二叉搜索树的最小绝对差(530题)
题目描述:
给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。

递归法: 1.首先可以中序遍历,因为是二叉搜索树,有序,中序遍历之后是一个单调递增的数组,在进行处理就很简单了
class Solution {
//递归中序遍历求一个数组接收中序遍历的数
private:vector<int>vec;void traversal(TreeNode* root){if(root == NULL)return ;traversal(root->left);//左vec.push_back(root->val);//中traversal(root->right);//右}
public:int getMinimumDifference(TreeNode* root) {vec.clear();traversal(root);int result = INT_MAX;//结果if(vec.size() < 2)return 0;//数组的大小小于2直接返回错位//对数组两个树的差进行运算取最小值for(int i = 1;i < vec.size();i++){result = min(result,vec[i] - vec[i-1]);}return result;}
};2.递归,使用的是两个节点思想来实现,双指针的思想可以实现
class Solution {
private:int result = INT_MAX;//定义一个最小值TreeNode* pre;//定义一个节点指向前一个节点位置void traversal(TreeNode* cur){if(cur == NULL)return ;//终止条件traversal(cur->left);//左//前一个指针现在为空,当后面赋值之后不为空,在进行比较if(pre != NULL){result = min(result,cur->val - pre->val);//前一个节点和当前节点值相减比较取最小值}pre = cur;//赋值当前节点traversal(cur->right);//右}
public:int getMinimumDifference(TreeNode* root) {traversal(root);return result;}
};迭代法:也是中序遍历
class Solution {
public:int getMinimumDifference(TreeNode* root) {stack<TreeNode*>st;TreeNode* cur = root;TreeNode* pre = NULL;int result = INT_MAX;while(cur != NULL || !st.empty()){if(cur != NULL){st.push(cur);cur = cur->left;}else{cur = st.top();st.pop();if(pre != NULL){result = min(result,cur->val - pre->val);}pre = cur;cur = cur->right;}}return result;}
};5.二叉搜索树中的众数(501题)
题目描述:
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
- 结点左子树中所含结点的值小于等于当前结点的值
- 结点右子树中所含结点的值大于等于当前结点的值
- 左子树和右子树都是二叉搜索树
递归法:普通二叉树做法,并且使用哈希表来实现,把这个树都遍历了,用map统计频率,把频率排个序,最后取前面高频的元素的集合。
class Solution {
//递归方法
private://如果按照普通二叉树的方法来实现,需要一个哈希表,对这个数据的数值进行统计void searchbst(TreeNode* cur,unordered_map<int,int>& map){if(cur == NULL)return ;map[cur->val]++;//中处理逻辑,每个节点进行哈希表记录数值searchbst(cur->left,map);//左searchbst(cur->right,map);//右return ;}//自定义一个比较的规则,比较哈希表排序,第一个最大bool static cmp(const pair<int,int>& a,const pair<int,int>& b){return a.second > b.second;//}
public:vector<int> findMode(TreeNode* root) {unordered_map<int,int>map;//哈希表vector<int>result;if(root == NULL)return result;//节点为空,返回searchbst(root,map);//递归vector<pair<int,int>>vec(map.begin(),map.end());//把哈希表的值放到数组里,不能直接排序sort(vec.begin(),vec.end(),cmp);//排序数组result.push_back(vec[0].first);//第一个放到结果里//取出现频率最高的元素放入result数组里for(int i = 1;i < vec.size();i++){if(vec[i].second == vec[0].second){result.push_back(vec[i].first);}else{break;}}return result;}
};二叉搜索树的方法:弄一个指针指向前一个节点,这样每次cur(当前节点)才能和pre(前一个节点)作比较。而且初始化的时候pre = NULL,这样当pre为NULL时候,我们就知道这是比较的第一个元素。清空数组那步很绝,最大频率更新把数组清空再放入新的数,
class Solution {
private:int maxcount;//最大频率int count;//统计频率TreeNode* pre;//前一个节点vector<int>result;//结果//中序遍历,二叉搜索树特性,有序,void searchbst(TreeNode* cur){if(cur == NULL)return ;//终止条件searchbst(cur->left);//左//第一个节点,记录频率1if(pre == NULL){count = 1;}else if(pre->val == cur->val){count++;//前一个节点和当前节点值相等,频率+1}else{count = 1;//不同时候,频率为1}pre = cur;//更新上一个节点,其实和双指针没什么差别//如果频率和最大值相同,都加入数组中if(count == maxcount){result.push_back(cur->val);}//如果频率大于最大值if(count > maxcount){maxcount = count;//更新最大频率result.clear();//清空数组这步很关键result.push_back(cur->val);}searchbst(cur->right);//右return ;}
public:vector<int> findMode(TreeNode* root) {count = 0;maxcount = 0;TreeNode* pre = NULL;//记录前一个节点result.clear();searchbst(root);return result;}
};迭代法:中序遍历转迭代法,其中处理逻辑没什么变化
class Solution {
public:vector<int> findMode(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;TreeNode* pre = NULL;int maxCount = 0; // 最大频率int count = 0; // 统计频率vector<int> result;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点,访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left; // 左} else {cur = st.top();st.pop(); // 中if (pre == NULL) { // 第一个节点count = 1;} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}if (count == maxCount) { // 如果和最大值相同,放进result中result.push_back(cur->val);}if (count > maxCount) { // 如果计数大于最大值频率maxCount = count; // 更新最大频率result.clear(); // 很关键的一步,不要忘记清空result,之前result里的元素都失效了result.push_back(cur->val);}pre = cur;cur = cur->right; // 右}}return result;}
};6.二叉树的最近公共祖先(236题)
题目描述:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
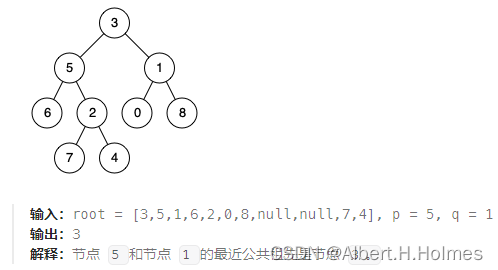
递归:首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。后序遍历回溯方法来实现
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == q || root == p || root == NULL)return root;//终止条件TreeNode* left = lowestCommonAncestor(root->left,p,q);//本题需要递归返回值,但是需要遍历整颗树,需要判断左右完成递归TreeNode* right = lowestCommonAncestor(root->right,p,q);//右if(left != NULL && right != NULL)return root;//左右子树不为空,返回根节点if(left == NULL && right != NULL)return right;//左子树为空,右子树else if(left != NULL && right == NULL)return left;//左节点不为空,返回左节点else{return NULL;//否则返回空}}
};需要搞清楚递归逻辑,以及遍历整颗树,还有回溯的后序遍历过程。
7.二叉搜索树的最近公共祖先(235题)
题目描述:
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
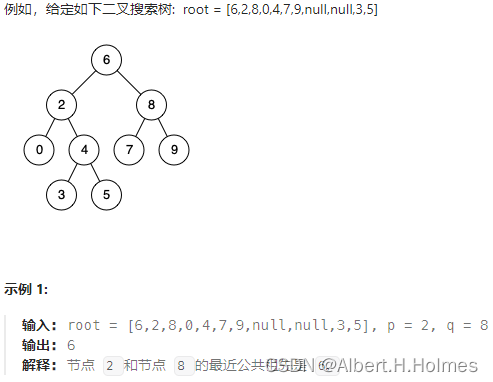
递归法: 从上向下去递归遍历,第一次遇到 cur节点是数值在[q, p]区间中,那么cur就是 q和p的最近公共祖先。需要注意的是此时不知道p和q谁大,所以两个都要判断
class Solution {
private://这里我们找到值立刻返回,二叉搜索树是一个有序树,我们前序遍历即可实现,从上到下递归,找到节点在q和p之间就返回TreeNode* traversal(TreeNode* cur,TreeNode* p,TreeNode* q){if(cur == NULL)return NULL;//终止条件//当前节点的值大于左右节点,向左递归if(cur->val > p->val && cur->val > q->val){TreeNode* left = traversal(cur->left,p,q);//左if(left != NULL){return left;//返回左}}//当前节点的值小于左右节点,向右递归if(cur->val < p->val && cur->val < q->val){TreeNode* right = traversal(cur->right,p,q);//右if(right != NULL){return right;//返回右}}return cur;}
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {return traversal(root,p,q);}
};迭代法:节点如果当前节点大于pq值左边迭代,反之,最后找到根节点返回,没找到返回空
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {while(root) {if (root->val > p->val && root->val > q->val) {root = root->left;} else if (root->val < p->val && root->val < q->val) {root = root->right;} else return root;}return NULL;}
};总结:
合并二叉树:遍历一个树逻辑是一样的,只不过传入两个树的节点,同时操作,注意终止条件如果一空返回2,2空返回1,我们可以在1树上进行操作即可实现前序遍历即可,层序遍历也可以实现模版,注意需要考虑节点空的情况即可
二叉搜索树中的搜索,二叉搜素树特性,左子树小于根节点, 右子树大于根节点,有序树,这里需要注意有返回值去接收,二叉搜索树不要队列或者栈也可以实现迭代,不需要辅助就可以完成
验证二叉搜索树:因为二叉搜索树的特性是一个有序树,可以遍历,中序让节点值放入数组,自然升序,判断是否升序就可以实现了,节点方法:注意需要定义一个指针这个指针需要走当前节点的前一个节点,pre=cur注意,先判断pre=null时候,在执行,迭代法中序实现即可,
二叉搜索树的最小绝对差:数组的方法也是一样的,寻找两个节点之间的最小差值即可,依然中序遍历,节点法:也是需要定义一个节点去走当前节点上一个节点,然后进行差值比较就可以实现,注意pre的赋值就可以中序遍历,迭代法:中序遍历
二叉搜索树的众数:普通二叉树的话,需要使用哈希表来结合,我们遍历整个树,然后使用map去对键值对进行记录,然后利用数组pair进行接收,排序,取最高频率元素即可实现,二叉搜索树的方法:也是双指针,就是再来一个节点记录当前走过的前一个节点的位置,然后比较两个节点是否相等,相等进行操作,记录频率,和最大频率,这里需要注意最大频率如果出现更新需要对数组清除然后再已添加元素,仍然使用中序遍历法,迭代法:其实没什么差别使用
二叉树的最近公共祖先:这里需要注意递归函数需要返回值,找到就需要返回,需要后序遍历进行到二叉树的根节点,这里需要注意中间节点的处理方法,需要判断左右节点的是否为空,再进行处理,需要遍历整棵树的逻辑,
二叉搜索树的最近公共祖先:二叉搜索树是有序树,前序遍历就可以实现,从上到下递归,终止条件需要注意,这里需要判断当前节点的值和左右节点的值进行对比,如果在这个区间就直接返回,迭代法:节点如果当前节点大于pq值左边迭代,反之,最后找到根节点返回,没找到返回空



![[嵌入式软件][入门篇] 搭建在线仿真平台(STM32)](https://img-blog.csdnimg.cn/direct/85f410f7b42a4e71afba3bcf3412d136.png)