使用pytorch构建线性回归模型
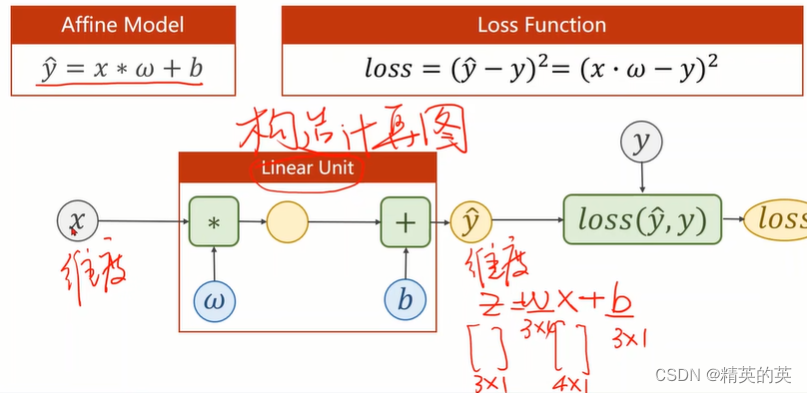
线性方程的一般形式

衡量线性损失的一般形式-均方误差

pytorch中计算图的作用和优势
在 PyTorch 中,计算图(Computational Graph)是一种用于表示神经网络运算的数据结构。每个节点代表一个操作,例如加法、乘法或激活函数,而边则代表这些操作之间的数据流动。
计算图的主要优点是可以自动进行微分计算。当你在计算图上调用 .backward() 方法时,PyTorch 会自动计算出所有变量的梯度。这是通过使用反向传播算法来实现的,该算法从最后的输出开始,然后根据链式法则回溯到输入。
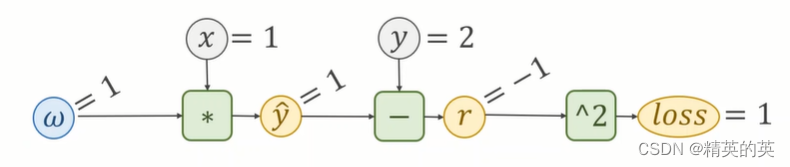
以下是一个简单的计算图示例:
import torch# 定义两个张量
x = torch.tensor([1.0], requires_grad=True)
y = torch.tensor([2.0], requires_grad=True)# 定义计算图
z = x * y
out = z.mean()# 计算梯度
out.backward()print(x.grad) # tensor([0.5])
print(y.grad) # tensor([0.5])
在这个例子中,我们首先定义了两个需要求导的张量 x 和 y。然后,我们定义了一个计算图,其中 z 是 x 和 y 的乘积,out 是 z 的平均值。当我们调用 out.backward() 时,PyTorch 会自动计算出 x 和 y 的梯度。
注意,只有那些设置了 requires_grad=True 的张量才会被跟踪并存储在计算图中。这样,我们就可以在需要时计算这些张量的梯度。
import torchx_data = [1.0, 2.0, 3.0] #x输入,表示特征
y_data = [2.0, 4.0, 6.0] #y输入,表示标签w = torch.tensor([1.0], requires_grad=True) #创建权重张量,启用自动计算梯度def forward(x): #前向传播return x * w #特征和权重的点积,构建乘法计算图def loss(x, y):y_pred = forward(x)return (y_pred - y) ** 2 #均方误差,构建损失计算图
线性模型的计算图的一般形式
print("predict before training is {}".format(forward(4).item()))for epoch in range(100):for x,y in zip(x_data, y_data):#组合特征和标签l = loss(x,y) #定义计算图,包括前向传播和计算损失l.backward() #反向传播,计算梯度print("\tgrad:", x,y,w.grad.item())#梯度的标量w.data = w.data - 0.01 * w.grad.data#使用“.data”表示是更新数据,而不是创建计算图w.grad.data.zero_()#梯度清零,准备创建下一个计算图print("progress:", epoch, l.item())
print("predict after training:{}".format(forward(4).item()))
使用pytorch API
pytorch的张量计算

准备数据集
x_data = torch.tensor([[1.0],[2.0],[3.0]])
y_data = torch.tensor([[2.0],[4.0],[6.0]])
class LinearModel(torch.nn.Module):def __init__(self, *args, **kwargs) -> None:super(LinearModel, self).__init__(*args, **kwargs)self.linear = torch.nn.Linear(in_features=1, out_features=1)def forward(self, x):y_pred = self.linear(x)return y_predmodel = LinearModel()
定义损失函数和损失优化函数
关于小批量随机梯度下降
小批量随机梯度下降(Mini-batch Stochastic Gradient Descent)是批量梯度下降的一种变体。与批量梯度下降相比,小批量随机梯度下降在每次迭代时只使用一小部分数据(称为小批量)来计算梯度,然后根据这个梯度来更新模型的参数。
小批量随机梯度下降的目标函数为:
J ( θ ) = 1 m ∑ i = 1 m L ( y ( i ) , f θ ( x ( i ) ) ) J(\theta) = \frac{1}{m} \sum_{i=1}^{m} L(y^{(i)}, f_{\theta}(x^{(i)})) J(θ)=m1i=1∑mL(y(i),fθ(x(i)))
其中, J ( θ ) J(\theta) J(θ) 是目标函数, m m m 是数据集的大小, L ( y ( i ) , f θ ( x ( i ) ) ) L(y^{(i)}, f_{\theta}(x^{(i)})) L(y(i),fθ(x(i))) 是第 i i i 个样本的损失函数, f θ ( x ( i ) ) f_{\theta}(x^{(i)}) fθ(x(i)) 是模型对第 i i i 个样本的预测。
小批量随机梯度下降的更新规则为:
θ = θ − α ∇ J ( θ ) \theta = \theta - \alpha \nabla J(\theta) θ=θ−α∇J(θ)
其中, α \alpha α 是学习率, ∇ J ( θ ) \nabla J(\theta) ∇J(θ) 是目标函数关于 θ \theta θ 的梯度。
小批量随机梯度下降的优点是它结合了批量梯度下降的优点(即可以利用整个数据集的信息来更新参数)和随机梯度下降的优点(即可以在每次迭代时使用新的数据)。这使得它在处理大规模数据集时具有更好的计算效率,同时也能避免随机梯度下降的问题(即可能会陷入局部最优)。
criteria = torch.nn.MSELoss()#使用均方误差做损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)#使用随机梯度下降做损失优化函数
for epoch in range(1000):y_pred = model(x_data)loss = criteria(y_pred, y_data)print(epoch, loss)optimizer.zero_grad()#梯度清零loss.backward()#反向传播optimizer.step()#梯度下降更新参数
预测
print("w=", model.linear.weight.item())
print("b=", model.linear.bias.item())x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print("y_pred=", y_test.data)
print("w=", model.linear.weight.item())
print("b=", model.linear.bias.item())
实践
使用pytorch创建线性模型进行波士顿房价预测(数据集可以自行下载)
import pandas as pd
import numpy as np
import torch
import matplotlib.pyplot as pltdata_file = "J:\\MachineLearning\\数据集\\housing.data"pd_data = pd.read_csv(data_file, sep="\s+")def prepare_data(data, normalize_data=True): # 标准化特征矩阵(可选) if normalize_data: features_mean = np.mean(data, axis=0) #特征的平均值features_dev = np.std(data, axis=0) #特征的标准偏差features_ret = (data - features_mean) / features_dev #标准化数据else: features_mean = None features_dev = None return features_retnp_data = pd_data.sample(frac=1).reset_index(drop=True).values
#bias = np.ones(len(np_data)).reshape(-1,1)
#np_data = np.concatenate((bias, np_data), axis=1)
train_data = np_data[:int(len(np_data)*0.8), :]test_data = np_data[int(len(np_data)*0.8):, :]
train_dataset = train_data[:, :-1]
test_dataset = test_data[:, :-1]
train_labels = train_data[:, -1]
test_labels = test_data[:, -1]
train_dataset = prepare_data(train_dataset)
# Save the mean and standard deviation of the target variable before normalization
target_mean = np.mean(train_labels)
target_dev = np.std(train_labels)print(np_data.shape)
print(train_data.shape)
print(train_dataset.shape)
print(train_labels.shape)features = torch.tensor(train_dataset, dtype=torch.float32)
print(features[:10])
feature_num = features.shape[1]
labels = torch.tensor(train_labels.reshape(-1,1), dtype=torch.float32)print(features.shape)
print(labels.shape)class LinearReg(torch.nn.Module):def __init__(self, *args, **kwargs) -> None:super(LinearReg, self).__init__(*args, **kwargs)self.linear_reg = torch.nn.Linear(in_features=feature_num, out_features=1)def forward(self, x):pred_y = self.linear_reg(x)return pred_yepoch = 100000
lr = 0.001
linear_model = LinearReg()
loss_function = torch.nn.MSELoss(size_average=True)
optimizer = torch.optim.SGD(linear_model.parameters(), lr)loss_history = []
last_loss = 0.01
for epoch_step in range(epoch):predict = linear_model(features)loss = loss_function(predict, labels)if (epoch_step % 100 == 0):print(epoch_step, loss)loss_history.append(loss.item())if (abs(float(loss.item()) - last_loss)/last_loss < 0.00001):breaklast_loss = float(loss.item())optimizer.zero_grad()loss.backward()optimizer.step()plt.plot(loss_history)
plt.show()
test_dataset = prepare_data(test_dataset)
test_dataset = torch.tensor(test_dataset, dtype=torch.float32)
result = linear_model(test_dataset).detach().numpy()
predicted_values = np.round(result, 2)
print(predicted_values)
show_result = np.concatenate((predicted_values.reshape(-1,1), test_labels.reshape(-1,1)), axis=1)
print(show_result)
print(predicted_values)