前言
这篇博客针对河北大学 大数据分析与挖掘 课程期末复习,目的是给同学们一个比较清晰的复习方向,具体的学习还需要平时认真听讲、写作业。
我们使用的教材是这本:
练习题目
我只更新了部分答案,至于剩下的答案 老师上课的时候会带着讲解的。在这里 我只是为同学们提供一个复习纲要和复习方向。希望大家能快速抓到考试重点,不在其他方向上浪费精力。

选择题答案: 1.C 2.D

判断题答案:1.X 2.√ 3.X 4.X (若答案有误 ,请及时联系我)



(二)答案&步骤:



(四)答案&解题步骤:

大题






复习大纲
第一章
>4V理论(p1):1.容量volume 2.多样性variety 3.速度velocity 4.价值value
第二章
>数据属性的类型(p17): 1.标称属性(离散、分类) 2.序数属性(离散、分类) 3.数值属性(连续)
>描述数据集中趋势的度量(p20):1.算术平均数 2.中位数 3.众数 4.k百分位数
>描述数据离中趋势的度量(p22):1.极差 2.四分位数极差 3.平均绝对离差 4.方差和标准差 5.离散系数
>数据分布特征可视化(p27):1.箱型图 2.正态分布
>相关分析(p31):
1.散点图
2.相关系数:(只适用于数值型(连续值))
首先了解协方差,给定n个样本,属性X和Y之间的样本协方差计算公式:

协方差可以反映两个属性在变化过程中的变化情况。若同时变大,协方差就是正的;若一个属性变大,另一个属性变小,协方差就是负的。协方差的正负代表两个属性相关性的方向,而协方差的绝对值代表它们之间关系的强弱。
样本相关系数的计算公式:
相关系数消除了两个属性量纲的影响。
3.卡方检验(适用于离散值(标称属性))
卡方统计量:
Observed:观测值/实际值
Expected:期望值/理论值
实际值与理论值偏差越大,就越大,表明越不符合;偏差越小,
就越小,越趋于符合;若两值完全相等,
就为0.
>数据预处理(p35):
1.零均值化: 给定一个数值型数据集合,将每一个属性的数据都减去属性的均值。零均值变换后,各属性的方差不发生变化,协方差也不变。
2. Z分数变换(Z-score变换):
s为标准差。Z分数变换可以消除量纲不一致的影响。
3.最小-最大规范化(离差标准化):
将数据按比例缩放至一个特定区间。假设原来数据分布在区间[min,max],要变换到区间[min' , max'],公式如下:
4.独热编码(适用于标称属性)
>PCA主成分分析(必考)p42:
目的与基本思想:
目的就是降维。用较少数量的不相关的维度代替原来的维度,并能够解释数据所包含的大部分信息,这些不相关的新维度称为主成分。主成分是一种降维方法,将p维特征映射到m维上(m<p)
步骤:
假设样本包含n个p维数据,我们想要降维到m个主成分。
(1)将样本数据表示成列向量形式,即
,此时X为一个p*n维矩阵,每一行代表一个属性
(2)将X的每一维进行零均值化
(3)求样本协方差矩阵C
(4)计算协方差矩阵C的特征值
,及对应的标准正交特征向量。
(5)将特征向量按照对应的特征值大小从大到小排列成矩阵。
(6)将样本投影到新的坐标系上,取方差占比例最大的主成分作为新的主成分即可。
最后得到的主成分F是一个线性相关公式。
>数据清洗(p49)
1.缺失值填充:均值填充 回归填充 热卡填充(找到一个与它最相似的对象,用相似对象的值来填充)
2.平滑噪声:(p51)
分箱:等深分箱 等宽分箱
将数据分箱后对每个分箱中的数据进行局部平滑:
1.平均值平滑 2.边界值平滑 3.中值平滑
第三章 关联规则挖掘
以下内容在p60
>频繁k-项集:频繁项集元素个数为k
>支持度计数:记录项集X出现过的次数
>支持度及最小支持度:
比如:{面包、啤酒、奶酪}这个三项集,在总共N=6次的购买记录里,同时出现了3次,,支持度计数为3,则支持度为3/6 = 50%。
最小支持度minsup:这是主观条件,可自己设定。当sup(X)>=minsup时,项集X为频繁项集。
>关联规则:形如,A,B是不相交的项集。
>关联规则的支持度:
>置信度:
通常会给出最小置信度,同时满足最小支持度和最小置信度的关联规则称为强关联规则。
>关联规则挖掘的一般过程:
1.通过最小支持度,找到所有的频繁项集 2.根据最小置信度,过滤频繁项集产生的所有关联规则
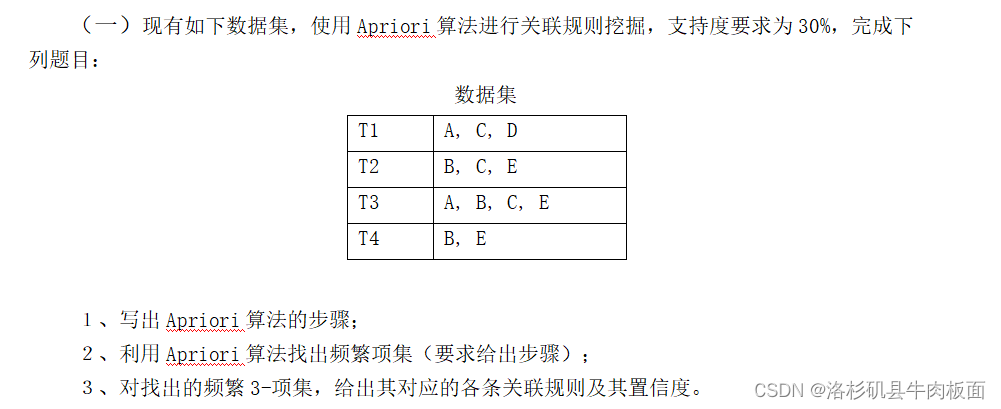
>Apriori算法(p61)
>FP-Growth算法(P66)
这两个算法看B站视频UP主讲解,很清晰明了,可以快速上手。链接放在下面,
数据挖掘期末必考计算题之FP growth,看这个就过了_哔哩哔哩_bilibili
FPgrowth例题计算(保护脖子版本)_哔哩哔哩_bilibili
期末数据挖掘关联规则的apriori 算法计算大题_哔哩哔哩_bilibili
数据仓库 数据挖掘 关联规则挖掘 - Apriori 算法_哔哩哔哩_bilibili
后面几章的重点就是 (都是2021届考过的):
>K-means算法、DBSCAN算法
>ID3和C4.5算法
>异常点检测
这是2023-2024秋学期 考试中涉及到的知识点,我做了笔记:

这块就不细细更新了,大家平时好好听课,做题。