Java浮点数精度问题与BigDecimal详解-编程知识

第1章：引言

大家好，我是小黑，咱们在日常的Java编程中，经常会遇到处理金融数据的情况，比如计算商品的价格或者处理用户的账户余额。在这些场景下，精确的数值计算就显得尤为重要。这时候，BigDecimal就成了咱们的好帮手。不像普通的float和double类型，BigDecimal提供了非常精确的数值计算。

但为什么要用BigDecimal而不是普通的double或者float呢？举个例子，假设咱们用double类型来计算0.1加上0.2，结果竟然是0.30000000000000004！这样的精度误差在金融计算中是绝对不能接受的。这就是为什么在处理这类问题时，咱们需要一个更加可靠的工具，而BigDecimal正好满足这个需求。

第2章：BigDecimal基础

首先咱们得搞清楚，BigDecimal到底是个什么东东。简单来说，BigDecimal是Java提供的一个类，它可以处理超大或者超精确的浮点数。这个类里面有一堆方法，可以让咱们进行精确的数学运算，而不会像double和float那样有精度损失的问题。

来，咱们先看看怎么创建一个BigDecimal对象。咱们通常有两种方式来创建BigDecimal：一种是使用字符串构造器，另一种是直接使用数字。但这里有个小陷阱，如果直接使用数字构造器，有时候会出现不精确的问题。比如说，使用new BigDecimal(0.1)创建的BigDecimal其实是不精确的，它的内部值会是0.1000000000000000055511151231257827021181583404541015625，这可不是咱们想要的。所以，在实际应用中，小黑更推荐使用字符串构造器来创建BigDecimal对象。

// 使用字符串构造器创建BigDecimal
BigDecimal a = new BigDecimal("0.1");
BigDecimal b = new BigDecimal("0.2");// 输出结果
System.out.println("a的值是：" + a);
System.out.println("b的值是：" + b);

上面的代码中，咱们创建了两个BigDecimal对象，a和b，值分别是0.1和0.2。用字符串构造器创建的BigDecimal就能避免使用数字构造器时的精度问题。

好，接下来咱们看看如何进行基本的数学运算。BigDecimal提供了add、subtract、multiply和divide等方法，让咱们可以执行加、减、乘、除等操作。

// 加法运算
BigDecimal sum = a.add(b);
System.out.println("a加b的结果是：" + sum);// 减法运算
BigDecimal difference = a.subtract(b);
System.out.println("a减b的结果是：" + difference);// 乘法运算
BigDecimal product = a.multiply(b);
System.out.println("a乘b的结果是：" + product);// 除法运算
BigDecimal quotient = a.divide(b, 2, RoundingMode.HALF_UP);
System.out.println("a除以b的结果是（保留两位小数）：" + quotient);

在上面的代码中，咱们使用了BigDecimal类的add、subtract、multiply和divide方法进行了基本的数学运算。特别注意的是，在进行除法运算时，咱们需要指定精度和舍入模式，这里咱们保留两位小数，使用的是四舍五入的方式。

第3章：创建BigDecimal对象

咱们先来说说最常见的创建方式：使用字符串来构造BigDecimal。可能有人会问，为啥要用字符串，直接用数字不行吗？这其实是因为用数字直接创建BigDecimal时，可能会引入一些意想不到的精度问题。这是因为浮点数在计算机中的表示本身就可能是不精确的。比如，0.1 在计算机中可能会被表示为一个接近但不完全等于0.1的值。所以，当咱们用这种方式创建BigDecimal时，实际上是在用一个已经存在精度问题的值来初始化它，这显然不是咱们想要的。

来，看看下面这个例子：

// 错误的创建方式：直接使用double值
BigDecimal incorrect = new BigDecimal(0.1);
System.out.println("直接使用double创建的BigDecimal：" + incorrect);// 正确的创建方式：使用字符串
BigDecimal correct = new BigDecimal("0.1");
System.out.println("使用字符串创建的BigDecimal：" + correct);

在这个例子中，咱们可以看到直接用0.1这个double值创建的BigDecimal和用字符串"0.1"创建的BigDecimal是不一样的。直接用double值创建出来的BigDecimal其实已经不是精确的0.1了。

除了用字符串构造器，咱们还可以用BigDecimal.valueOf方法来创建BigDecimal对象。这个方法在内部其实是先把double转换成String，然后再用这个String来创建BigDecimal。这样做就避免了直接用double值带来的精度问题。

// 使用BigDecimal.valueOf创建BigDecimal
BigDecimal valueOfExample = BigDecimal.valueOf(0.1);
System.out.println("使用BigDecimal.valueOf创建的BigDecimal：" + valueOfExample);

以上就是创建BigDecimal对象的两种主要方式。记住，虽然直接使用数字构造器看起来更直接，但为了避免精度问题，咱们应该优先考虑使用字符串构造器或者BigDecimal.valueOf方法。

第4章：BigDecimal的数学运算

加法（Addition）

加法可能是最基础的运算了。在BigDecimal中，咱们用add方法来实现加法。看下面这个例子：

// 创建两个BigDecimal对象
BigDecimal num1 = new BigDecimal("10.05");
BigDecimal num2 = new BigDecimal("20.75");// 加法运算
BigDecimal sum = num1.add(num2);
System.out.println("加法结果：" + sum); // 输出30.80

在这个例子中，咱们把10.05和20.75两个数加在一起，得到了30.80。这种计算方式比起普通的double或float来说，精度高得多。

减法（Subtraction）

减法跟加法差不多简单。咱们用subtract方法来执行减法。来看个例子：

// 减法运算
BigDecimal difference = num2.subtract(num1);
System.out.println("减法结果：" + difference); // 输出10.70

这里咱们用20.75减去10.05，得到的结果是10.70，没有任何精度损失。

乘法（Multiplication）

乘法在BigDecimal中是用multiply方法实现的。但要注意，乘法结果的精度会受到操作数精度的影响。看下面这个例子：

// 乘法运算
BigDecimal product = num1.multiply(num2);
System.out.println("乘法结果：" + product); // 输出208.3875

在这个例子中，10.05乘以20.75的结果是208.3875。BigDecimal在这里展示了其精确处理小数点后位数的能力。

除法（Division）

除法可能是BigDecimal中最复杂的运算，因为它涉及到了舍入模式和除不尽的情况。在使用divide方法时，咱们通常需要指定精度和舍入模式。看这个例子：

// 除法运算
BigDecimal quotient = num1.divide(num2, 2, RoundingMode.HALF_UP);
System.out.println("除法结果：" + quotient); // 输出0.48

这里咱们把10.05除以20.75，结果保留两位小数，采用四舍五入的方式。如果不指定精度和舍入模式，当结果无法精确表示时，就会抛出异常。

通过这些例子，咱们可以看出，BigDecimal提供了非常强大和灵活的数学运算能力。不过，正因为其操作略显复杂，所以在使用时需要更加小心，以确保计算结果的准确性。这也是为什么在进行金融计算时，选择使用BigDecimal而不是普通的浮点类型非常重要的原因之一。

第5章：精度问题深入分析

精度问题的根源

要理解BigDecimal的精度问题，咱们得知道它是如何存储数值的。BigDecimal实际上是通过一个不可变的、任意精度的有符号十进制数来表示数值的。它由两部分组成：一个整数非标度值和一个32位的整数标度（scale）。比如，数值10.05可以表示为1050 * 10^-2，这里1050是非标度值，-2是标度。

这种表示方式让BigDecimal能够提供准确的小数运算，但同时也带来了精度问题。尤其是在进行除法运算时，如果除不尽，就需要确定小数点后要保留多少位数，以及采用何种舍入模式。

精度控制

在使用BigDecimal进行计算时，精度控制非常关键。看看下面这个例子：

// 创建BigDecimal对象
BigDecimal num1 = new BigDecimal("1");
BigDecimal num2 = new BigDecimal("3");// 未指定精度的除法运算，可能会抛出异常
try {BigDecimal result = num1.divide(num2);System.out.println("除法结果：" + result);
} catch (ArithmeticException e) {System.out.println("精度问题导致的异常：" + e.getMessage());
}

在这个例子中，1除以3是无法得到一个精确的小数结果的，所以如果不指定精度和舍入模式，就会抛出ArithmeticException异常。为了解决这个问题，咱们可以在进行除法运算时指定精度和舍入模式。

// 指定精度的除法运算
BigDecimal resultWithPrecision = num1.divide(num2, 2, RoundingMode.HALF_UP);
System.out.println("指定精度的除法结果：" + resultWithPrecision); // 输出0.33

在这个例子中，咱们指定了小数点后保留两位，并使用了四舍五入的方式。这样就可以得到一个精确控制了精度的结果。

舍入模式的选择

在处理精度问题时，选择合适的舍入模式也很重要。BigDecimal提供了多种舍入模式，比如RoundingMode.HALF_UP（四舍五入）、RoundingMode.DOWN（直接舍弃多余的小数位）、RoundingMode.UP（远离零方向舍入）等。不同的场景可能需要不同的舍入策略，所以在实际应用中需要根据具体需求来选择。

复杂运算中的精度处理

在处理更复杂的运算，比如连续的乘除法，精度控制就显得更加重要。这时候，每一步运算的精度都可能影响到最终的结果。因此，咱们需要仔细规划每一步运算的精度，以确保整个计算过程中数值的精度符合预期。

综上所述，处理BigDecimal的精度问题需要对它的内部表示有一定的了解，并且在实际应用中谨慎地控制精度和选择适当的舍入模式。通过这些方法，咱们可以有效地解决在使用BigDecimal时遇到的

第6章：性能

性能影响因素

BigDecimal的性能影响因素主要包括：

对象的创建：由于BigDecimal是不可变对象，每次运算都会产生新的对象，这就意味着涉及频繁的内存分配和回收。
精度和舍入模式：高精度运算和复杂的舍入模式会增加计算的复杂度，从而影响性能。
复杂运算：比如连续的乘法和除法，这些操作在BigDecimal中更加消耗资源。

性能优化技巧

虽然BigDecimal在性能上有一定的开销，但是通过一些技巧，我们可以在一定程度上优化这些性能问题：

适当的精度：选择合适的精度进行计算，避免不必要的高精度运算。比如，在货币计算中通常保留两位小数就足够了。
重用对象：尽可能重用BigDecimal对象，比如将常用的数值（如0、1、10）作为常量使用。
减少不必要的运算：优化算法，减少不必要的运算，特别是避免在循环中创建大量的BigDecimal对象。

来看个简单的例子，展示如何优化性能：

// 常用BigDecimal值的重用
static final BigDecimal ZERO_POINT_ONE = new BigDecimal("0.1");
static final BigDecimal FIVE = new BigDecimal("5");public static void main(String[] args) {BigDecimal result = ZERO_POINT_ONE.multiply(FIVE);System.out.println("结果：" + result); // 输出0.5
}

在这个例子中，咱们通过定义常量来重用BigDecimal对象，这样就避免了每次计算时都创建新对象的开销。

虽然使用BigDecimal可以提供高精度的计算结果，但在性能方面确实有所牺牲。因此，在实际开发中，我们需要在精度和性能之间找到一个平衡点。特别是在处理大量运算或要求高性能的场景中，这种权衡尤为重要。通过合理的设计和优化，咱们可以在保证计算准确性的同时，也尽量减少性能上的损失。

第7章：实际应用案例

案例1：金融计算

在金融领域，精确的计算尤为重要，比如说在计算贷款利息、汇率转换或者投资回报时。举个例子，如果咱们要计算一个存款的年利息，假设年利率是3.5%，存款金额是10000元，那么一年的利息就可以用BigDecimal来精确计算。

// 年利率和存款金额
BigDecimal annualInterestRate = new BigDecimal("0.035");
BigDecimal depositAmount = new BigDecimal("10000");// 计算一年的利息
BigDecimal interest = depositAmount.multiply(annualInterestRate).setScale(2, RoundingMode.HALF_UP);
System.out.println("一年的利息是：" + interest + "元"); // 输出结果

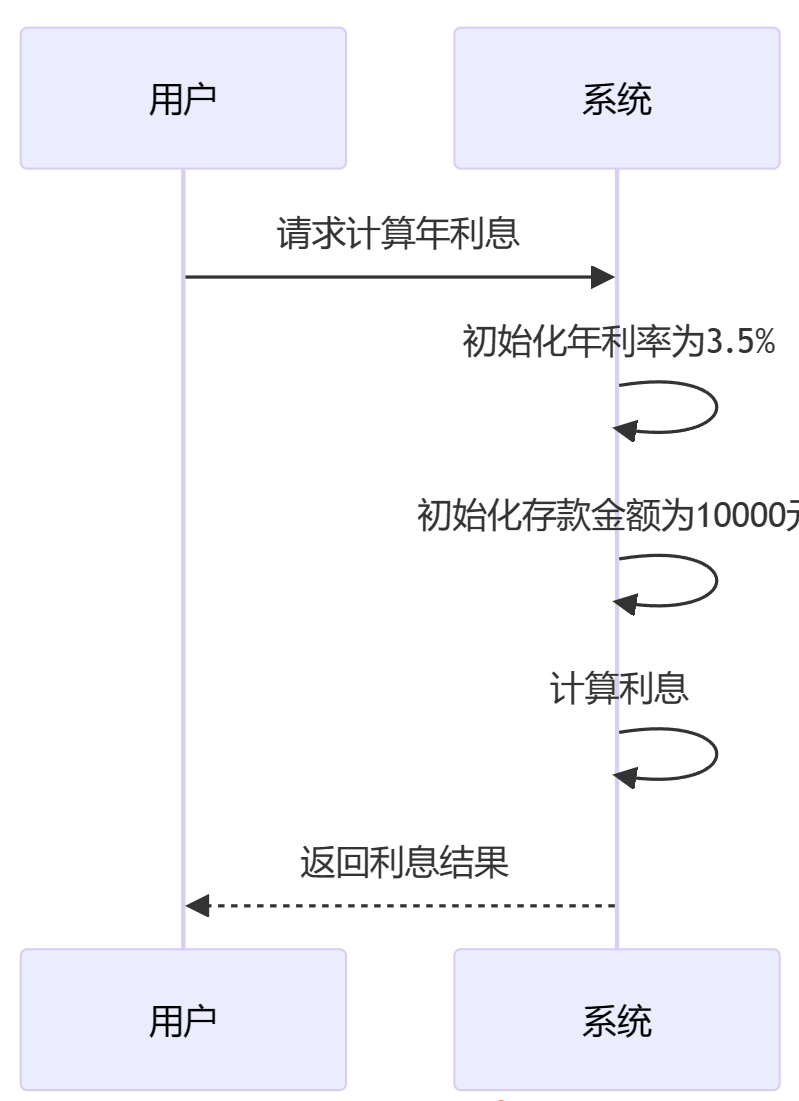
这个例子展示了如何使用BigDecimal进行精确的乘法运算，并通过setScale方法设置结果的小数位数和舍入模式。

案例2：商业账单处理

另一个常见的用例是在商业应用中处理账单。比如说，咱们需要计算一张含有多个商品的账单总额，其中涉及到商品数量和单价的乘法以及多个商品总价的加法。

// 商品单价和数量
BigDecimal priceOfItem1 = new BigDecimal("19.99");
BigDecimal quantityOfItem1 = new BigDecimal("2");
BigDecimal priceOfItem2 = new BigDecimal("45.50");
BigDecimal quantityOfItem2 = new BigDecimal("1");// 计算总价
BigDecimal totalOfItem1 = priceOfItem1.multiply(quantityOfItem1).setScale(2, RoundingMode.HALF_UP);
BigDecimal totalOfItem2 = priceOfItem2.multiply(quantityOfItem2).setScale(2, RoundingMode.HALF_UP);
BigDecimal totalBill = totalOfItem1.add(totalOfItem2);
System.out.println("账单总额是：" + totalBill + "元"); // 输出结果

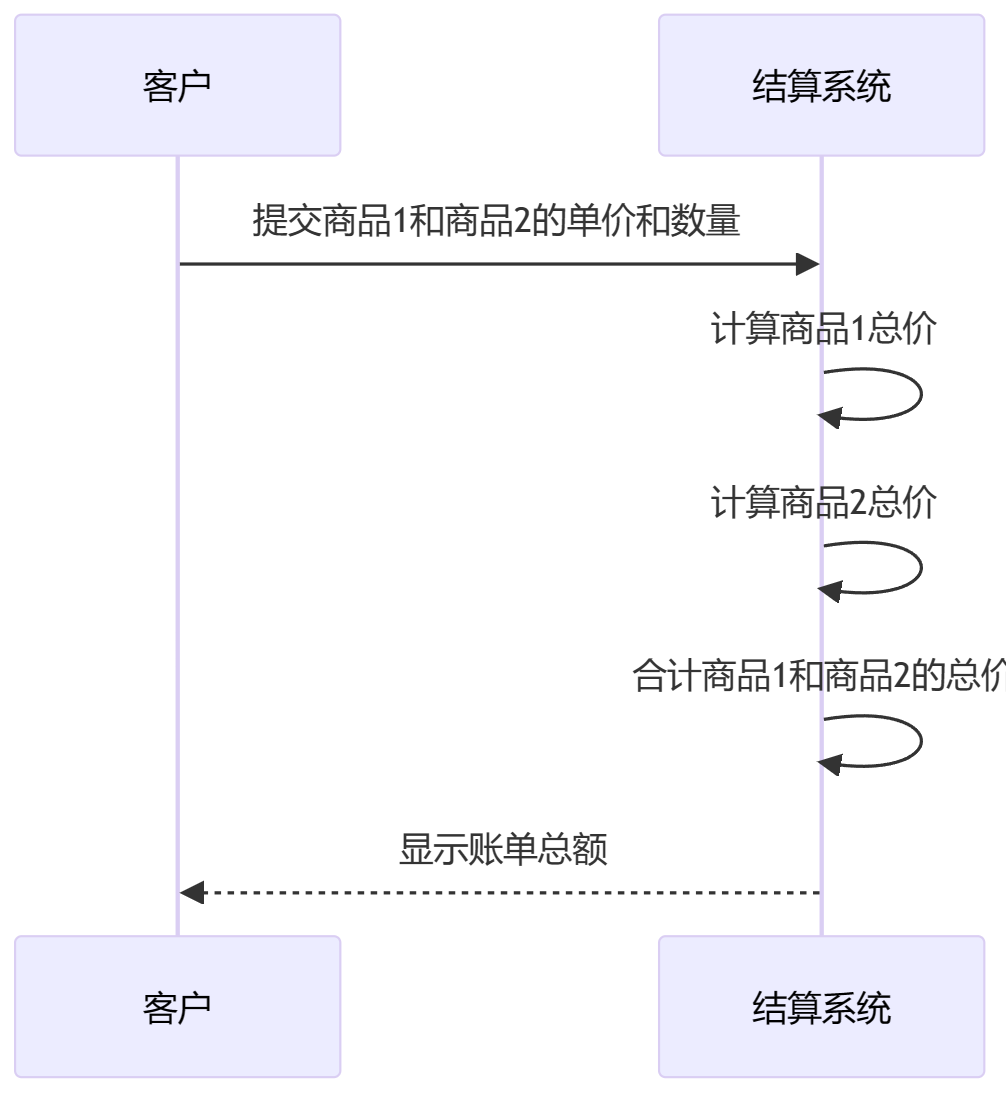
在这个例子中，咱们用BigDecimal来处理每个商品的总价计算，并且精确地得出了整张账单的总金额。

案例3：科学计算

BigDecimal不仅在金融和商业领域有用，在需要高精度计算的科学领域也同样重要。比如在物理或工程学中，精确计算某些公式的结果。

// 计算某个科学公式（示例）
BigDecimal a = new BigDecimal("1.2345");
BigDecimal b = new BigDecimal("6.7890");
BigDecimal c = a.multiply(b).add(new BigDecimal("3.21")).setScale(5, RoundingMode.HALF_UP);
System.out.println("科学计算结果：" + c); // 输出结果