引言
传统的深度神经网络一般都有过度自信的问题。
即使我给神经网络提供一个从来没有训练过的类别图像,神经网络也会输出一个类别。比如训练猫狗的分类器,如果你抛出一个人的图像,网络也会将其分类为猫或者狗。
在几乎所有现实世界的问题中,我们想要的不仅仅是结果,还需要对该结果的信心/确定性的了解。如果正在制造自动驾驶汽车,不仅要检测行人,还要表达对该物体是行人而不是交通锥的信心。
在贝叶斯世界观中,一切都具有概率分布,包括模型参数(神经网络中的权重和偏差)。在编程语言中,我们有可以采用特定值的变量,每次访问该变量时,您都会获得相同的值。与此相反,在贝叶斯世界中,我们有类似的实体,称为随机变量,每次访问它时都会给出不同的值。
从随机变量中获取新值的过程称为采样。得出什么值取决于随机变量的相关概率分布。与随机变量相关的概率分布越宽,其值的不确定性就越大,因为它可以根据(宽)概率分布取任何值。
在传统的神经网络中,有固定的权重和偏差来确定输入如何转换为输出。
在贝叶斯神经网络中,所有权重和偏差都有一个概率分布。要对图像进行分类,需要对网络进行多次运行(前向传递),每次都使用一组新的采样权重和偏差。
每次运行得到一组,得到多组输出值。输出值集表示输出值的概率分布,因此可以找出每个输出的置信度和不确定性。所以,对输入图像是网络从未见过的东西,那么对于所有输出类别,不确定性将会很高。
贝叶斯定理:
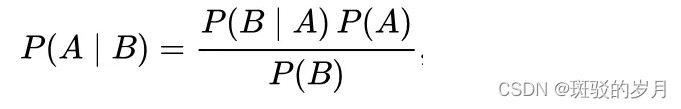
A:神经网络参数 (权重和偏差的初始概率分布)
B:训练数据
使用数据来找出权重和偏差的更新分布P(A | B)。
P(A):神经网络参数的先验。
P(B|A):在给定参数,我们可以多次运行(前向传递),每次都使用一组新的采样权重和偏差。每次运行得到一组,得到多组输出值,输出值集表示输出值的概率分布。

P(B)计算很困难,在所有可能的参数值下观察数据(输入/输出对)的概率,并按各自的概率加权。 evidence
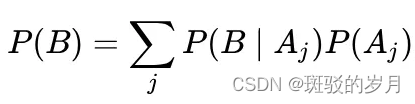
-
参数Aj的值范围可以从 负无穷大到 正无穷大
-
对于该范围内的每个Aj值,您必须运行模型来查找生成您观察到的输入、输出对的可能性(总数据集可能有数百万对)
-
这样的参数可能不止一个,而是很多个 (可能上百万)
上面是后验的枚举方法,还有其他方法
- 基于抽样的方法 蒙特卡罗方法( Monte-Carlo )
对于复杂的贝叶斯模型,例如具有 800 万个参数的神经网络,蒙特卡罗方法的收敛速度仍然很慢,并且可能需要数周时间才能发现完整的后验。 - 优化方法:变分贝叶斯
P(z|x)在分布空间中,在这个分布空间的一个分布族Q,找一个分布q*∈Q与P(z|x)的距离最近。
找一个q*∈Q去估计P(z|x)
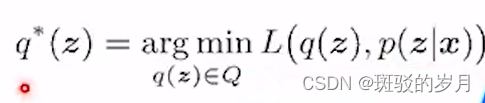
L经常用KL散度,两个分布差异的度量。
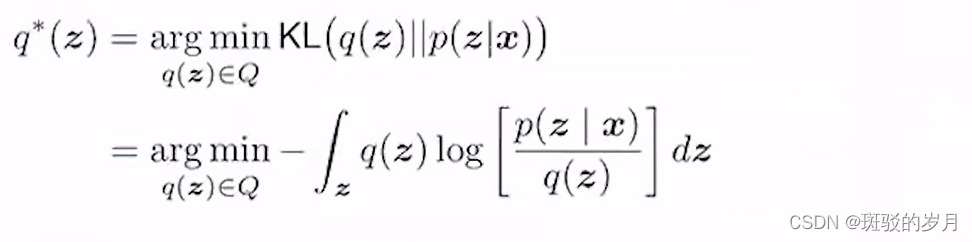
这个是不能直接计算的,因为P(z|x)是未知,进行转化:
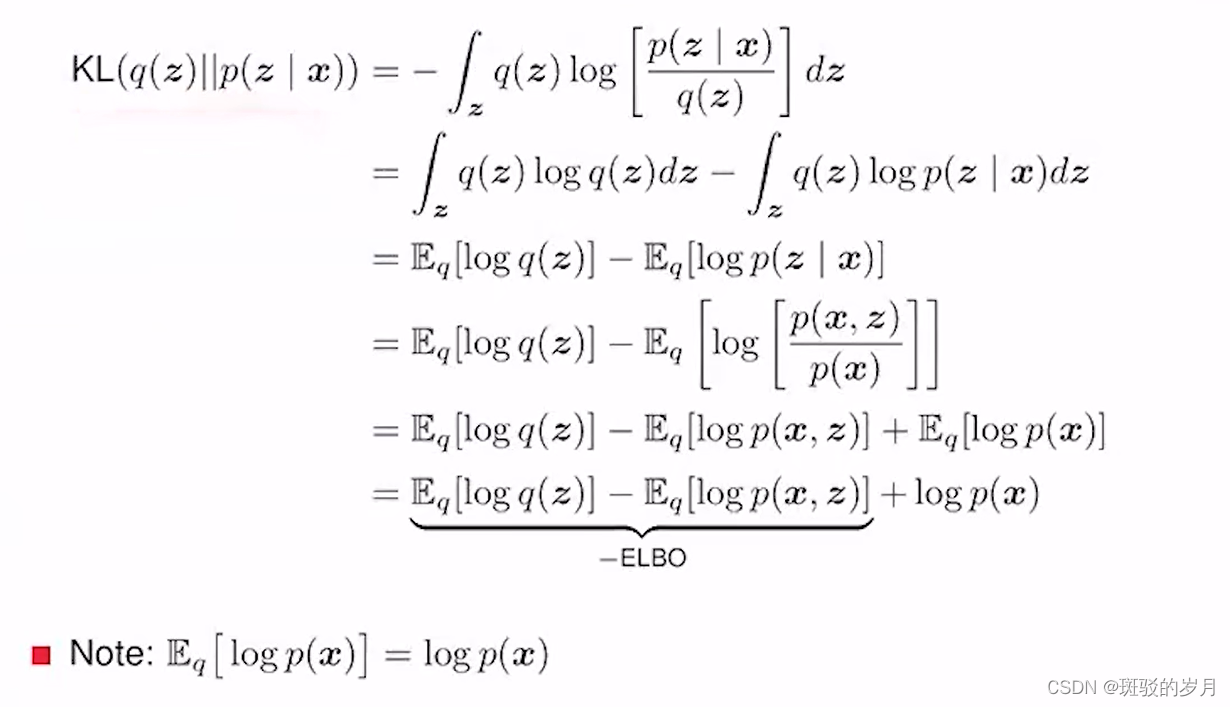
ELBO evidence lower bound,
KL 大于等于0 ,logp(x) constant ;evidence
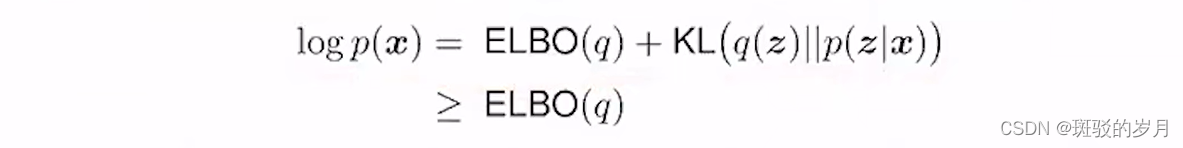
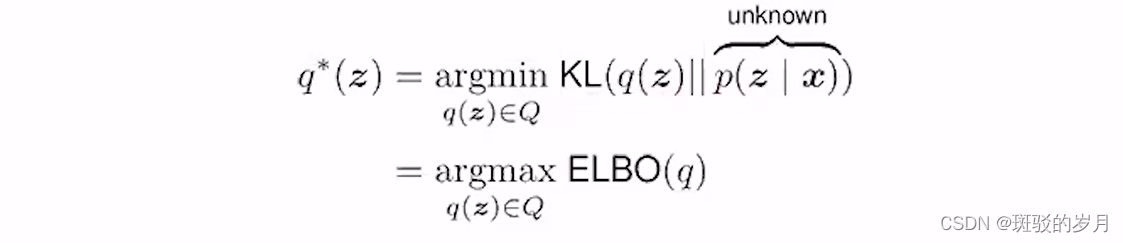
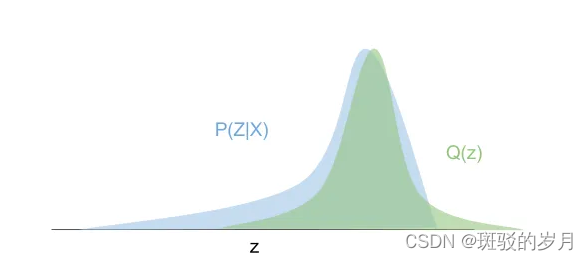
变分贝叶斯方法的要点是由于我们无法精确计算后验概率,因此我们可以找到最接近它的“行为良好”的概率分布。在“行为良好”的分布中随机初始化参数后,可以进行梯度下降并每次稍微修改分布的参数(例如均值或方差),以查看结果分布是否更接近后验分布。度量接近程度用ELBO.
蓝色曲线是进行(枚举)计算得到的真实后验。 因为他是一种像正态分布一样表现良好的分布,绿色曲线的整个形状可以用一个参数 Z 来描述。变分贝叶斯方法所做的是使用梯度下降方法来随机改变 Z 参数的值初始化值为其结果分布最接近真实后验的值。优化结束时,绿色曲线与蓝色曲线并不完全相同,但非常相似。我们可以安全地使用近似的绿色曲线而不是未知的真实蓝色曲线来进行预测。