C++力扣题目617--合并二叉树-编程知识

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

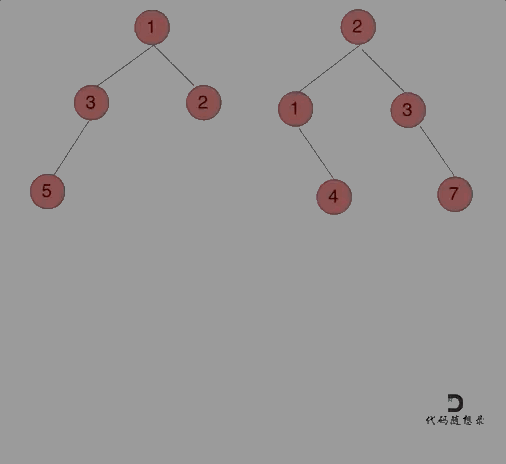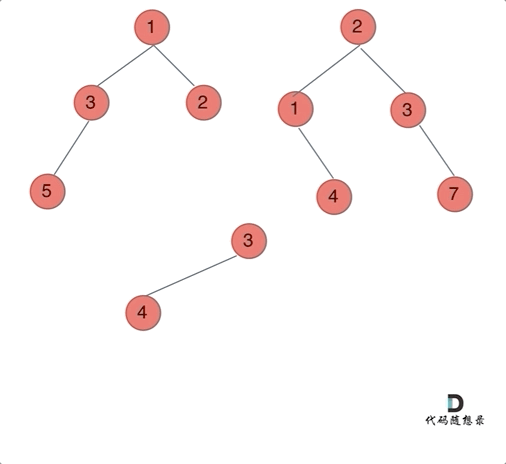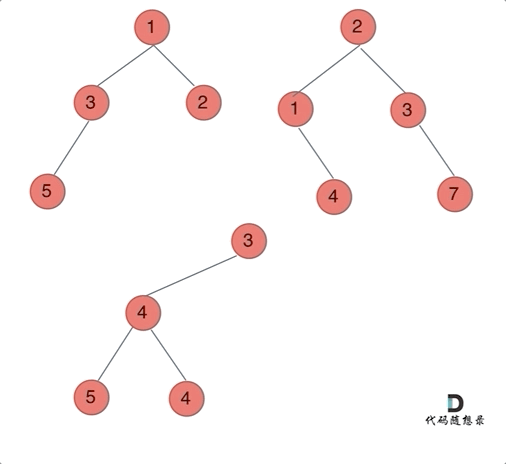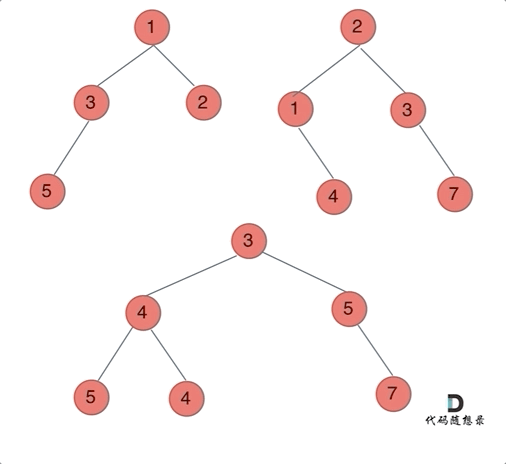
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

思路

相信这道题目很多同学疑惑的点是如何同时遍历两个二叉树呢？

其实和遍历一个树逻辑是一样的，只不过传入两个树的节点，同时操作。

#递归

二叉树使用递归，就要想使用前中后哪种遍历方式？

本题使用哪种遍历都是可以的！

我们下面以前序遍历为例。

动画如下：

617.合并二叉树

那么我们来按照递归三部曲来解决：

确定递归函数的参数和返回值：

首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。

代码如下：

TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {

确定终止条件：

因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了（如果t2也为NULL也无所谓，合并之后就是NULL）。

反过来如果t2 == NULL，那么两个数合并就是t1（如果t1也为NULL也无所谓，合并之后就是NULL）。

代码如下：

if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2
if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1

确定单层递归的逻辑：

单层递归的逻辑就比较好写了，这里我们重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。

那么单层递归中，就要把两棵树的元素加到一起。

t1->val += t2->val;

接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树。

t1 的右子树：是合并 t1右子树 t2右子树之后的右子树。

最终t1就是合并之后的根节点。

代码如下：

t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;

此时前序遍历，完整代码就写出来了，如下：

class Solution {
public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1// 修改了t1的数值和结构t1->val += t2->val;                             // 中t1->left = mergeTrees(t1->left, t2->left);      // 左t1->right = mergeTrees(t1->right, t2->right);   // 右return t1;}
};

那么中序遍历也是可以的，代码如下：

class Solution {
public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1// 修改了t1的数值和结构t1->left = mergeTrees(t1->left, t2->left);      // 左t1->val += t2->val;                             // 中t1->right = mergeTrees(t1->right, t2->right);   // 右return t1;}
};

后序遍历依然可以，代码如下：

class Solution {
public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1// 修改了t1的数值和结构t1->left = mergeTrees(t1->left, t2->left);      // 左t1->right = mergeTrees(t1->right, t2->right);   // 右t1->val += t2->val;                             // 中return t1;}
};

但是前序遍历是最好理解的，我建议大家用前序遍历来做就OK。

如上的方法修改了t1的结构，当然也可以不修改t1和t2的结构，重新定义一个树。

不修改输入树的结构，前序遍历，代码如下：

class Solution {
public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2;if (t2 == NULL) return t1;// 重新定义新的节点，不修改原有两个树的结构TreeNode* root = new TreeNode(0);root->val = t1->val + t2->val;root->left = mergeTrees(t1->left, t2->left);root->right = mergeTrees(t1->right, t2->right);return root;}
};

#迭代法

使用迭代法，如何同时处理两棵树呢？

思路我们在二叉树：我对称么？ (opens new window)中的迭代法已经讲过一次了，求二叉树对称的时候就是把两个树的节点同时加入队列进行比较。

本题我们也使用队列，模拟的层序遍历，代码如下：

class Solution {
public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2;if (t2 == NULL) return t1;queue<TreeNode*> que;que.push(t1);que.push(t2);while(!que.empty()) {TreeNode* node1 = que.front(); que.pop();TreeNode* node2 = que.front(); que.pop();// 此时两个节点一定不为空，val相加node1->val += node2->val;// 如果两棵树左节点都不为空，加入队列if (node1->left != NULL && node2->left != NULL) {que.push(node1->left);que.push(node2->left);}// 如果两棵树右节点都不为空，加入队列if (node1->right != NULL && node2->right != NULL) {que.push(node1->right);que.push(node2->right);}// 当t1的左节点 为空 t2左节点不为空，就赋值过去if (node1->left == NULL && node2->left != NULL) {node1->left = node2->left;}// 当t1的右节点 为空 t2右节点不为空，就赋值过去if (node1->right == NULL && node2->right != NULL) {node1->right = node2->right;}}return t1;}
};

#拓展

当然也可以秀一波指针的操作，这是我写的野路子，大家就随便看看就行了，以防带跑偏了。

如下代码中，想要更改二叉树的值，应该传入指向指针的指针。

代码如下：（前序遍历）

class Solution {
public:void process(TreeNode** t1, TreeNode** t2) {if ((*t1) == NULL && (*t2) == NULL) return;if ((*t1) != NULL && (*t2) != NULL) {(*t1)->val += (*t2)->val;}if ((*t1) == NULL && (*t2) != NULL) {*t1 = *t2;return;}if ((*t1) != NULL && (*t2) == NULL) {return;}process(&((*t1)->left), &((*t2)->left));process(&((*t1)->right), &((*t2)->right));}TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {process(&t1, &t2);return t1;}
};