题目:
给定一个包含非负整数的
m x n网格grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
示例:
示例 1:
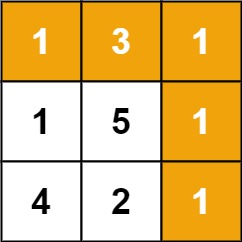
输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]] 输出:12
思想(动态规划)
动态规划是分治思想的延伸,通俗一点来说就是大事化小,小事化无的艺术
在将大问题化解为小问题的分治过程中,保存对着些小问题已经处理好的结果,并供后面处理更大规模的问题时直接使用这些结果
动态规划具备了以下三个特点
1.把原来的问题分解成了几个相似的子问题
2.所有的子问题都只需解决一次
3.存储子问题的解
动态规划的本质
是对问题状态的定义和状态转移方程的定义(状态以及状态之间的递推关系)
动态规划问题一般从以下四个角度考虑:
1.状态定义
2.状态间的转移方程定义
3.状态的初始化
4.返回结果
状态定义的要求:定义的状态一定要形成递推关系
适用场景:最大值/最小值 ,可不可行, 是不是,方案个数
算法分析与设计
步骤一、定义数组元素的含义
由于我们的目的是从左上角到右下角,最小路径和是多少,那我们就定义 dp[i] [j]的含义为:当走到(i, j) 这个位置时,最小的路径和是 dp[i] [j]。那么,dp[m-1] [n-1] 就是我们要的答案了。
注意,这个网格相当于一个二维数组,数组是从下标为 0 开始算起的,所以 由下角的位置是 (m-1, n - 1),所以 dp[m-1] [n-1] 就是我们要走的答案。
步骤二:找出关系数组元素间的关系式
一种是从 (i-1, j) 这个位置走一步到达
一种是从(i, j - 1) 这个位置走一步到达
不过这次不是计算所有可能路径,而是计算哪一个路径和是最小的,那么我们要从这两种方式中,选择一种,使得dp[i] [j] 的值是最小的,显然有
dp[i] [j] = min(dp[i-1][j],dp[i][j-1]) + arr[i][j];// arr[i][j] 表示网格种的值
步骤三、找出初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的,相当于计算机图中的最上面一行和左边一列。因此初始值如下:
dp[0] [j] = arr[0] [j] + dp[0] [j-1]; // 相当于最上面一行,只能一直往左走
dp[i] [0] = arr[i] [0] + dp[i] [0]; // 相当于最左面一列,只能一直往下走
代码实现
class Solution {public int minPathSum(int[][] grid) {int col=grid[0].length;int row=grid.length;if(row<0||col<0){return -1;}int[][] dp=new int[row][col];dp[0][0]=grid[0][0];for(int i=1;i<col;i++){dp[0][i]=grid[0][i]+dp[0][i-1];}for(int i=1;i<row;i++){dp[i][0]=grid[i][0]+dp[i-1][0];}for(int i=1;i<row;i++)for(int j=1;j<col;j++){dp[i][j]=Math.min(dp[i][j-1],dp[i-1][j])+grid[i][j];}return dp[row-1][col-1];}
}运行结果



![[C#]利用paddleocr进行表格识别](https://img-blog.csdnimg.cn/direct/ddca10cd7ff844ceac57722395c9d97c.jpeg)