1 Introduction

希望能用比较简单的方式将ilqr算法进行整理和总结。

2 HJB方程

假定我们现在需要完成一个从A点到B点的任务，执行这段任务的时候，每一步都需要消耗能量，可以用下面这个图表示。

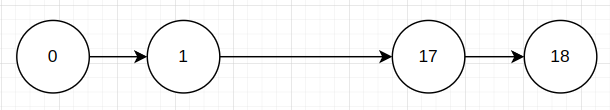
我们在执行这个A点到B点的任务的时候，需要建立一个评价评价系统，有了明显的评价指标，我们才能对各种决策进行对比。现在问题来了，应该选择什么样的数据作为评价指标。我们在构建我们的最优决策的时候，借用动态规划的思想，通过分解的方法去反向求解我们这个最优决策序列。显然我们会使用能量损耗作为评价指标(值函数)，我们希望用当前步开始，到终点所用的总能量最小。

$$V_{k-1}(x)=V_k(x)+loss（bellman方程）$$

这是一个离散的表达形式，在一个连续的系统上，上面这个公式可以看成是，从时间维度上能量消耗的速度 * 时间=单位距离能量消耗 * 距离，根据上面动态规划的策略，随着距离终点越远，我们的值函数是越大的，所以
$$\begin{array}{r}\frac{\partial V}{\partial s}{\Delta }_s+loss=0\\ \frac{\partial V}{\partial s}v\ast {\Delta }_t+loss速度\ast {\Delta }_t=0\\ \frac{\partial V}{\partial s}v+loss速度=0\end{array}$$
但是我们知道，这是我们在动态规划的贪婪策略下，才能取得的结果，并不是所有的u都能得到这样好的结果，所以有
min ⁡ u 0 { ∂ V ∂ s v + l o s s 速度 } = 0 \min_{u_0} \{ \frac{\partial V}{\partial s} v + loss速度 \}=0 u0​min​{∂s∂V​v+loss速度}=0

现在说了很多了，看起来和hamilton毫无关系。实际上ilqr推导过程中，使用了hamilonian变量就是
$$H=\frac{\partial V}{\partial s}v+loss速度(hamilon公式)$$
那么实际上HJB方程就是
$$\underset{u}{\min }H=0$$
如果hamilonian变量可导，这个公式可以拆成两个公式：
$$\begin{array}{rl}H& =0\\ \frac{\partial H}{\partial u}& =0(导数等于0，才能取到极值)\end{array}$$

3 LQR

在我们开始我们的推导之前，我们先把一些知识复习和梳理一下。
1）首先值函数V，可以看成是从当前状态到终点的损失累计J
2）LQR问题中，假定终点是无穷大时间，那么
$$J=\int (x_{ref}-x{)}^{T}Q(x_{ref}-x)+u^{T}Ru$$
3) 我们现在的瞬时loss(loss速度)是
$$g(x,u)=(x_{ref}-x{)}^{T}Q(x_{ref}-x)+u^{T}Ru$$
4) Hamilonian变量中的速度，一般由动力学系统(微分系统)给出。
$$\dot{x}=f(x,u)=A(x_{ref}-x)+Bu$$

那么HJB方程有
$$\begin{array}{rl}{\frac{\partial J}{\partial x}}^T(A(x_{ref}-x)+Bu)+(x_{ref}-x{)}^{T}Q(x_{ref}-x)+u^{T}Ru& =0\\ B\frac{\partial J}{\partial x}+2Ru& =0\end{array}$$
这个公式中$\frac{\partial J}{\partial x}$没法直接求，但是根据$J=\int (x_{ref}-x{)}^{T}Q(x_{ref}-x)+u^{T}Ru$，可以猜测

$$\frac{\partial J}{\partial x}=2S(x_{ref}-x)(有个2为了计算方便)$$
并且我们采用最简单的线性控制策略
$$u=K(x_{ref}-x)$$
我们把这两个假设代入到刚才那个方程中，虽然我们有两个未知量，但是我们有两个方程，大概率能求解。
$$\begin{array}{rl}2(x_{ref}-x{)}^T{S}^T(A(x_{ref}-x)+BK(x_{ref}-x))+(x_{ref}-x{)}^{T}Q(x_{ref}-x)+(x_{ref}-x{)}^T{K}^{T}RK(x_{ref}-x)& =0\\ 2BS(x_{ref}-x)+2RK(x_{ref}-x)& =0\end{array}$$
进行简化，得到
$$\begin{array}{rl}2SA+2SBK+Q+K^{T}RK& =0\\ K& =-R^{-1}BS\\ 2SA-2SB{R}^{-1}BS+Q+S{B}^T{R}^{-1}BS& =0\\ 2SA-SB{R}^{-1}BS+Q& =0\end{array}$$
这就是Ricaati方程，先把riccati方程借出来，得到S，然后再用$K =-R^{-1}BS $, 就能得到我们控制器所用的参数了。
注意，我这里推到和传统lqr推导不一样，我使用了 $x_{ref}-x$

最后我们总结一下，原来lqr，就是对HJB方程进行展开而已。

3 ilqr

ilqr 和lqr不同之处，在于需要在有限长度的情况下，做出决策。
对于当前状态的值函数，满足
$$J=\sum _0^{k-1}\{(x_{iref}-x_i{)}^{T}Q(x_{iref}-x_i)+u_i^{T}R{u}_i\}+(x_{kref}-x_k{)}^{T}Q(x_{kref}-x_k)+u_k^{T}R{u}_k$$

这个时候的Hamlitonian变量中的$\frac{\partial J}{\partial x}$，物理意义是单位距离内，能量的变化。[1]

因为
$$\frac{\partial P^k}{\partial u_k}=0$$
根据这个公式很容易推导得到8，
因为
$$V_x^k=\frac{\partial P^k}{\partial x_k}$$
并且因为${\delta }_{uk}$中有${\delta }_{xk}$的分量。
同理
$$V_{xx}^k=\frac{{\partial }^2{P}^k}{{\partial }^2{x}_k}$$

Reference

[1] Chen, Jianyu, Wei Zhan, and Masayoshi Tomizuka. “Autonomous driving motion planning with constrained iterative LQR.” IEEE Transactions on Intelligent Vehicles 4.2 (2019): 244-254.