蝴蝶效应的名字来源于蝴蝶扇动翅膀的动作，虽然这个动作微小，但可能会在数周后引起飓风等极端天气的发生。这种现象表明，微小的变化可能会被放大并产生非线性的结果。这个概念最早由美国气象学家爱德华·洛伦兹提出的。

Lorentz吸引子

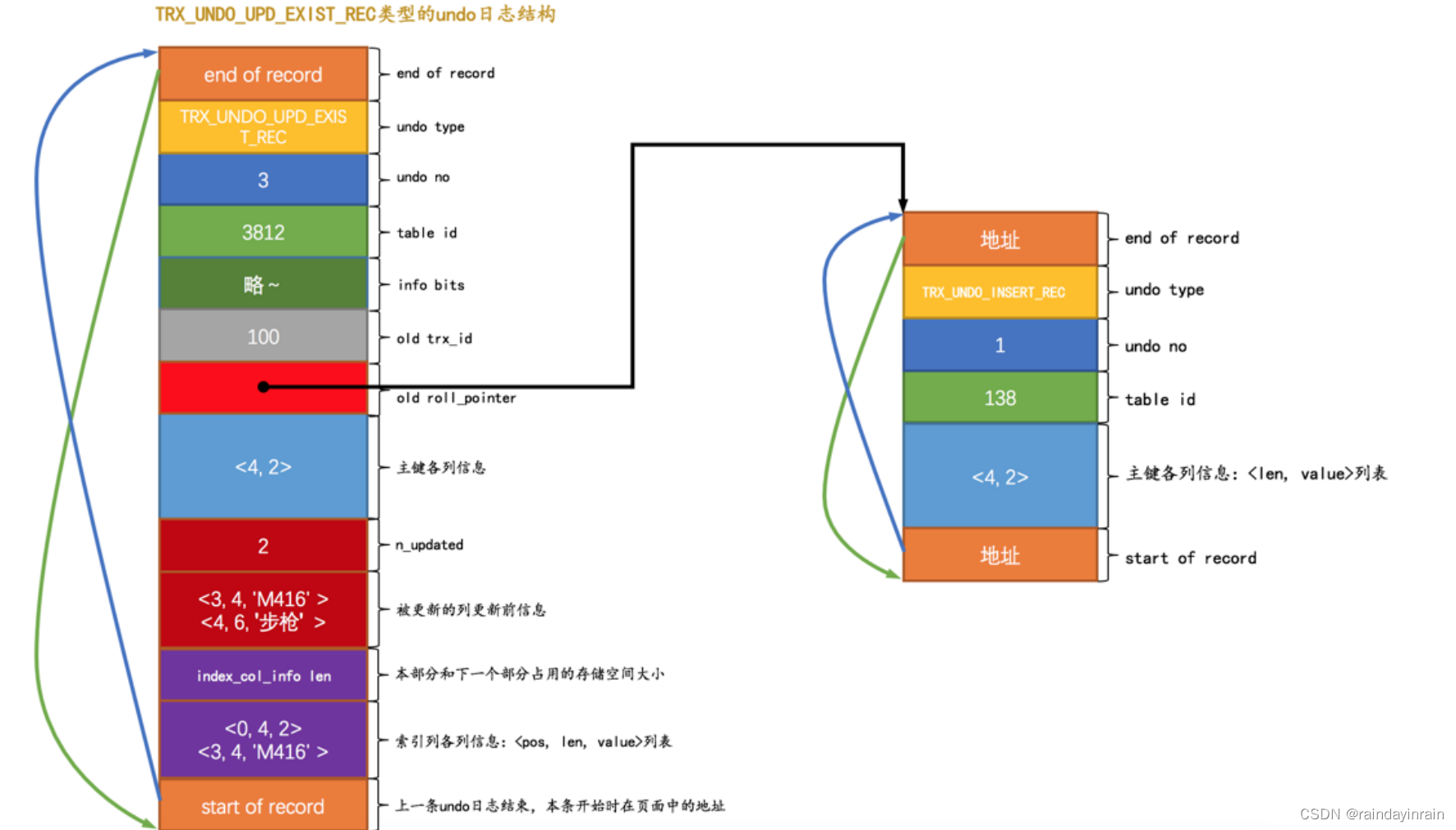
Lorentz吸引子堪称是微分方程组的经典入门案例了，图像也具有极高的辨识度，特别像蝴蝶的一对翅膀，同时与蝴蝶效应的内涵极为相称，表现出微小扰动可能带来巨大的差异性后果。

其方程为

$$\begin{array}{rl}\frac{\text{d}x}{\text{d}t}& =\sigma (y-x)\\ \frac{\text{d}y}{\text{d}t}& =x(\rho -z)-y\\ \frac{\text{d}z}{\text{d}t}& =xy-\beta z\end{array}$$

julia绘图

将其改写为Julia函数

function lorenz!(du,u,p,t)σ,ρ,β = pdu[1] = σ*(u[2]-u[1])du[2] = u[1]*(ρ-u[3]) - u[2]du[3] = u[1]*u[2] - β*u[3]
end

将初值$u_0$和参数$p$设为

u0 = [1.0,0.0,0.0]
p = (10,28,8/3)

走你

using DifferentialEquations         #导入微分方程包
tspan = (0.0,100.0)
prob = ODEProblem(lorenz!,u0,tspan,p)
sol = solve(prob)

绘图

using Plots; gr()
plot(sol,vars=(1,2,3))
savefig("ode_4.png")

关闭抗锯齿

当然这个图其实是开了“抗锯齿”的，由于sol的结果本身就是一组分立的量，所以关闭denseplot之后，可以看到

plot(sol,vars=(1,2,3),denseplot=false)
savefig("ode_5.png")

ParameterizedFunctions.jl中提供了一个非常便捷的宏ode_def，可以更加直观地把Lorentz方程写为参数形式

L = @ode_def Lorentz begindx = σ*(y-x)dy = x*(ρ -z)- ydz = x*y -β*z
end σ ρ βprob = ODEProblem(L,u0,tspan,p)
sol = solve(prob)
plot(sol,vars=(1,2,3))